V.6 The Central Limit Theorem
The central limit theorem is a fundamental result in probability concerning sums of independent random variables. Let X1, X2, . . . be independent and suppose that they are identically distributed. Suppose also that they have mean 0 and variance 1. Then X1 + · · · + Xn has mean 0 and variance n. (The variance is n because the Xi are independent.) Therefore, Yn = (X1 + · · · + Xn) / 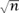 has mean 0 and variance 1. The central limit theorem states that, regardless of the distribution of the Xi, the random variable Yn converges to a standard normal distribution. It is easy to deduce from this a similar result for random variables with any finite mean and variance. Details may be found in PROBABILITY DISTRIBUTIONS [III.71 §5].
has mean 0 and variance 1. The central limit theorem states that, regardless of the distribution of the Xi, the random variable Yn converges to a standard normal distribution. It is easy to deduce from this a similar result for random variables with any finite mean and variance. Details may be found in PROBABILITY DISTRIBUTIONS [III.71 §5].
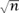 has mean 0 and variance 1. The central limit theorem states that, regardless of the distribution of the Xi, the random variable Yn converges to a standard normal distribution. It is easy to deduce from this a similar result for random variables with any finite mean and variance. Details may be found in PROBABILITY DISTRIBUTIONS [III.71 §5].
has mean 0 and variance 1. The central limit theorem states that, regardless of the distribution of the Xi, the random variable Yn converges to a standard normal distribution. It is easy to deduce from this a similar result for random variables with any finite mean and variance. Details may be found in PROBABILITY DISTRIBUTIONS [III.71 §5].