 (n!) elements, and is simple provided n ≥ 5. For example, A5, of order 60, is the smallest non-Abelian simple group.
(n!) elements, and is simple provided n ≥ 5. For example, A5, of order 60, is the smallest non-Abelian simple group.A finite group G is said to be simple if its only normal subgroups are the identity subgroup and G itself. To some extent, simple groups play an analogous role in finite group theory to that of prime numbers in number theory: just as the only factors of a prime p are 1 and p itself, so the only factor groups of a simple group G are the identity group 1 and G itself. The analogy runs a bit deeper: just as every positive integer (greater than 1) is a product of a collection of primes, so every finite group is “built” from a collection of simple groups, in the following sense. Let H be a finite group, and choose a maximal normal subgroup H1 of H (this means that H1 is not the whole of H, and it is not contained in any larger normal subgroup that is not the whole of H); then choose a maximal normal subgroup H2 of H1; and so on. This gives a sequence of subgroups 1 = Hr < Hr-1 < · · · < H1 < H0 = H, each one a maximal normal subgroup of the next, and, because of the maximality, each factor group Gi = Hi / Hi+1is a simple group. It is in this sense that one says that H is built from the collection G0, G1, . . ., Gr-1 of simple groups (although unlike the situation with prime numbers, there will in general be several different finite groups that are built from the same collection of simple groups).
At any rate, it is abundantly clear that simple groups lie at the heart of the theory of finite groups, and one of the driving forces of twentieth-century finite group theory was to study, and ultimately to classify completely, the finite simple groups. This classification was eventually achieved by the combined efforts of more than one hundred mathematicians in many published research articles and books written over a long period, the most intensive being 1955–80. It was a truly monumental feat of prolonged collaboration, and one of the most momentous theorems in the history of algebra.
In order to state the classification theorem, it is necessary to describe some examples of finite simple groups. The most obvious are the cyclic groups of prime order: these are clearly simple, since they have no subgroups at all apart from the identity and the whole group (by Lagrange’s theorem, for example, which states that the size of any subgroup is a factor of the size of the group). Next come the alternating groups An: here An is defined as the group consisting of all the even permutations in the symmetric group Sn (see PERMUTATION GROUPS [III.68]). The alternating group An has  (n!) elements, and is simple provided n ≥ 5. For example, A5, of order 60, is the smallest non-Abelian simple group.
(n!) elements, and is simple provided n ≥ 5. For example, A5, of order 60, is the smallest non-Abelian simple group.
Next we introduce some simple groups of matrices. For an integer n ≥ 2 and a field K, define SLn (K) to be the set of all n × n matrices with entries in K and with DETERMINANT [III.15] equal to 1. This is a group under matrix multiplication, called a special linear group. When the field K is finite, SLn(K) is a finite group. For each prime power q, there is up to isomorphism a unique field of order q, and the corresponding special linear group in dimension n is denoted by SLn( q). These groups are not in general simple, since Z = {λI : λn = 1}, the subgroup of scalar matrices in SLn(
q). These groups are not in general simple, since Z = {λI : λn = 1}, the subgroup of scalar matrices in SLn( q), is a normal subgroup. However, the factor groups PSLn(
q), is a normal subgroup. However, the factor groups PSLn( q) = SLn(
q) = SLn( q)/Z are simple (except when (n, q) = (2, 2) or (2, 3)). This is the family of projective special linear groups.
q)/Z are simple (except when (n, q) = (2, 2) or (2, 3)). This is the family of projective special linear groups.
There are a number of other families of finite simple matrix groups, which, very roughly speaking, are defined as groups of matrices A ∈ SLn( q) that satisfy an equation of the form ATJA = J, where J is a nonsingular symmetric or skew-symmetric n × n matrix. Again factoring out by the subgroup of scalar matrices, this gives the projective orthogonal and symplectic families of finite simple matrix groups. Similarly, if the finite field of order q has an automorphism α →
q) that satisfy an equation of the form ATJA = J, where J is a nonsingular symmetric or skew-symmetric n × n matrix. Again factoring out by the subgroup of scalar matrices, this gives the projective orthogonal and symplectic families of finite simple matrix groups. Similarly, if the finite field of order q has an automorphism α → 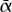 of order 2, this can be extended to matrices A = (aij) by defining
of order 2, this can be extended to matrices A = (aij) by defining 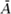 = (
= (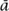 ij), and then the group {A ∈ SLn(
ij), and then the group {A ∈ SLn( q) : AT
q) : AT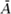 = I}, factored by its subgroup of scalar matrices, gives the projective unitary family of finite simple groups.
= I}, factored by its subgroup of scalar matrices, gives the projective unitary family of finite simple groups.
The families of projective special linear, symplectic, orthogonal, and unitary groups comprise what are known as the classical simple groups. These were all known early in the twentieth century, but it was not until 1955 that further infinite families of finite simple groups were discovered by Chevalley. For each of the simple complex Lie algebras L, and each finite field K, Chevalley constructed a version of L over K, call it L (K), and defined his families of finite simple groups as automorphism groups of the Lie algebras L(K). Not long afterward, Steinberg, Suzuki, and Ree found some variations of Chevalley’s construction and defined some further families of simple groups, known as twisted Chevalley groups. The Chevalley and twisted Chevalley groups include all the classical groups, together with ten other infinite families, and are collectively known as the finite simple groups of Lie type.
Until 1966, the only known finite simple groups were the cyclic groups of prime order, the alternating groups, the groups of Lie type, and a collection of five strange simple groups discovered by MATHIEU [VI.51] in the 1860s. These were groups of permutations of n objects, where n = 11, 12, 22, 23, or 24. Mathieu’s groups were termed “sporadic groups”—sporadic meaning that they do not fit into any of the known infinite families—and many thought that perhaps there were no more finite simple groups to be found. Then there was a bombshell, when Janko published a paper demonstrating the existence of a single, new finite simple group: the sixth sporadic group. After this, new sporadic groups appeared at regular intervals, culminating in the MONSTER [III.61], an amazing group of order around 1054, which was predicted by Fischer and constructed by Griess as a group of 196 884 × 196 884 matrices. By 1980, twenty-six sporadic groups were known.
During this period the program to classify all the finite simple groups was proceeding at breakneck speed, and eventually in the early 1980s the final classification theorem was announced.
Every finite simple group is either a cyclic group of prime order, or an alternating group, or a group of Lie type, or one of the twenty-six sporadic groups.
Not surprisingly, this theorem has changed the face of finite group theory and its many areas of application: one can now solve many problems in a concrete way, by reducing them to the study of the (now known) list of simple groups, rather than abstractly, by deducing them from the axioms for groups.
The sheer length of the proof of the classification theorem (estimated at around ten thousand journal pages, spread across about five hundred research articles) meant that it was extremely difficult, perhaps impossible, for a single person to work through the entire proof. It also meant that the chances were rather high that there were errors along the way. Fortunately, in the years since the announcement of the result, various teams of group theorists have been publishing summaries and revisions of many parts of the proof, and a series of volumes containing the whole proof is now well on the way to completion.