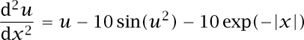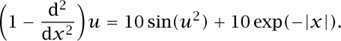V.11 Fixed Point Theorems
1 Introduction
The following is a variant of a well-known mathematical puzzle. A man is on a train from London to Cambridge and has a bottle of water with him. Prove that there is at least one moment on the journey when the volume of air in the bottle, as a fraction of the volume of the bottle itself, is exactly equal to the fraction of his journey that he has completed. (For instance, the bottle might be two fifths full, and therefore three fifths empty, at the precise moment when he is three fifths of the way from London to Cambridge. Note that we do not assume that the bottle is full at the start of the journey or empty at the end.)
The solution, if you have not seen this sort of question before, is surprisingly simple. For each x between 0 and 1 let f(x) be the proportion of air in the bottle when the proportion of the journey that has been completed is x. Then 0 ≤ f(x) ≤ 1 for every x, since the volume of air in the bottle cannot be negative and cannot exceed the volume of the bottle. If we now set g (x) to be x – f(x), then we see that g(0) ≤ 0 and g(1) ≥, 0. Since g(x) varies continuously with x, there must be some moment at which g(x) = 0, so that f(x) = x, which is what we wanted.
What we have just proved is a slightly disguised form of one of the simplest of all fixed point theorems. We could state it more formally as follows: if f is a continuous function from the closed interval [0, 1] to itself, then there must exist an x such that f(x) = x. This x we call a fixed point of f. (We deduced the result from the intermediate value theorem, a basic result in analysis that states that if g is a continuous function from [0, 1] to ℝ such that g(0) ≥ 0 and g(1) ≤ 0, then there must be some x such that g(x) = 0.)
In general, a fixed point theorem is a theorem that asserts that a function that satisfies certain conditions must have a fixed point. There are many such theorems, a small sample of which we shall discuss in this article. On the whole, they tend to have a nonconstructive nature: they establish the existence of a fixed point rather than defining one or telling you how to find it. This is part of the reason that they are important, since there are many examples of equations for which one would like to prove that a solution exists even when one cannot solve it explicitly. As we shall see, one way of going about this is to try to rewrite the equation in the form f(x) = x and apply a fixed point theorem.
2 Brouwer’s Fixed Point Theorem
The fixed point theorem we have just proved is the one-dimensional version of Brouwer’s fixed point theorem, which states that if Bn is the unit ball of ℝn (that is, the set of all (x1, . . ., xn) such that 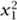 + · · · +
+ · · · + 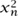 ≤ 1) and f is a continuous function from Bn to Bn, then f must have a fixed point. The set Bn is an n-dimensional solid sphere, but all that matters is its topological character, so we could take it to be another shape such as an n-dimensional cube or simplex.
≤ 1) and f is a continuous function from Bn to Bn, then f must have a fixed point. The set Bn is an n-dimensional solid sphere, but all that matters is its topological character, so we could take it to be another shape such as an n-dimensional cube or simplex.
In two dimensions this says that a continuous function from the closed unit disk to itself must have a fixed point. In other words, if you had a circular sheet of rubber on a table and you picked it up and put it back down within the circle where it started, having folded it and stretched it as much as you liked, there would always have to be a point that ended up in the same place as before.
To see why this is true, it is helpful to reformulate the statement. Let D = B2 be the closed unit disk. If we had a continuous function f from D to D with no fixed point, then we could define a continuous function g from D to its boundary ∂D as follows: for each x, follow a straight path from f(x) to x and continue on in a straight line; g (x) is the point where you first reach ∂ D (see figure 1), and it is well-defined because (and only because) f (x) ≠ x. If x is already on the boundary of D, then g(x) = x. So we have a continuous function g : D → ∂D such that g(x) = x for every x ∈ ∂D. Such a function is called a retraction from D to ∂D.
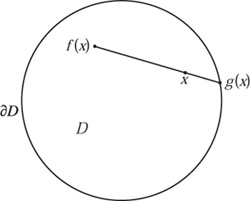
Figure 1 If f has no fixed points, then it can be used to define a retraction g.
It seems highly unlikely that a continuous retraction from D to ∂D could exist. If we can prove that it cannot, then we will have contradicted the assumption that there is a continuous function from D to D with no fixed point, and thereby have proved Brouwer’s fixed point theorem in two dimensions.
There are several ways of proving that continuous retractions from disks to their boundaries cannot exist. Here we briefly sketch two.
Suppose, first, that g is such a retraction. For each t, let us consider the restriction of g to the circle of radius t about the origin, and let us represent a typical point in this circle as teiθ. Let us write gt(θ) for g(teiθ). When t = 1 the circle of radius t is ∂ D, so as θ goes from 0 to 2π, gt (θ) = eiθ goes once around the unit circle. When t = 0, the circle of radius t is a single point, so as θ goes from 0 to 2π, gt(θ) is just the constant point g(0), which does not go around the unit circle at all. Therefore, somewhere between t = 1 and t = 0 there must be a change in the number of times gt (θ) goes around the unit circle as θ goes from 0 to 2π. But the functions gt are a continuously varying family of functions, and a small change in gt cannot cause a sudden jump in the number of times that gt(θ) goes around the circle. (To make this last step rigorous needs a bit of work, but the basic idea is sound.)
A second proof uses basic tools from algebraic topology. The first HOMOLOGY GROUP [IV.6 §4] of the disk D is trivial, since every curve in the disk can be shrunk to a point. The first homology group of the unit circle ∂D is ℤ. If there is a continuous retraction g from D to ∂D, then we can find continuous maps h: ∂D → D and g: D → ∂D such that g  h is the identity on ∂D. (We let h be the map that takes a point of ∂D to itself and we let g be the continuous retraction.) Now continuous maps between topological spaces give rise to HOMOMORPHISMS [I.3 §4.1] between their homology groups, in such a way that compositions go to compositions and identity maps go to identity maps. (That is, there is a FUNCTOR [III.8] from the CATEGORY [III.8] of topological spaces and continuous maps to the category of groups and group homomorphisms.) This means that there must be homomorphisms ϕ: ℤ → {0} and ψ : {0} → ℤsuch that ψ
h is the identity on ∂D. (We let h be the map that takes a point of ∂D to itself and we let g be the continuous retraction.) Now continuous maps between topological spaces give rise to HOMOMORPHISMS [I.3 §4.1] between their homology groups, in such a way that compositions go to compositions and identity maps go to identity maps. (That is, there is a FUNCTOR [III.8] from the CATEGORY [III.8] of topological spaces and continuous maps to the category of groups and group homomorphisms.) This means that there must be homomorphisms ϕ: ℤ → {0} and ψ : {0} → ℤsuch that ψ  ϕ is the identity on ℤ, which is obviously impossible.
ϕ is the identity on ℤ, which is obviously impossible.
Both proofs generalize to higher dimensions: the second straightforwardly (once one knows how to compute homology groups of spheres), and the first via the notion of the degree of a continuous map from the n-sphere to itself, which is a higher-dimensional analogue of the notion of the number of times a map from the circle to itself “goes around the circle.”
Brouwer’s fixed point theorem has many applications. For example, the following fact is important in the theory of random walks on graphs. A stochastic matrix is an n × n matrix with nonnegative entries such that the sum of the entries in each row is equal to 1. Brouwer’s fixed point theorem can be used to show that every such matrix has an EIGENVECTOR [I.3 §4.3] with nonnegative entries and eigenvalue 1. The proof is as follows: the set of all column vectors with nonnegative entries that add up to 1 is, geometrically speaking, an (n – 1)-dimensional simplex. (For example, if n = 3, this set is a triangle in ℝ3 with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1).) If A is a stochastic matrix and x belongs to this simplex, then so does Ax. Since the map x ↦ Ax is continuous, Brouwer’s theorem gives us an x such that Ax = x: this is the required eigenvector.
An extension of Brouwer’s theorem, called the Kakutani fixed point theorem, was used by John Nash to establish the existence of a “social equilibrium,” a state of affairs in which no household can individually improve its well-being by altering the amount that it consumes of various items. Kakutani’s theorem concerns functions that take points in a closed ball Bn not to other points in Bn but to subsets of Bn. If f (x) is a nonempty closed convex subset of Bn for each x and if f (x) varies continuously in an appropriate sense, then the theorem says that there must be some x such that x ∈ f (x). Brouwer’s theorem is the special case where each f (x) is a set with just one element.
3 A Stronger Form of Brouwer’s Fixed Point Theorem
So far, we have discussed maps from solid spheres to themselves, but there is nothing to stop us thinking about whether continuous maps on other spaces must have fixed points. For example, let S2 be the (nonsolid) sphere {(x, y, z) : x2 + y2 + z2 = 1} and let f be a continuous function from S2 to S2. Must f have a fixed point? At first one might think so: some obvious functions from S2 to itself are rotations and reflections, both of which certainly have fixed points, and it is hard to see how one can “get rid” of those fixed points. However, eventually one realizes that there is a simple example of a function without a fixed point, namely the function f (x) = –x, which reflects each point through the origin.
The obvious reaction to this example is to note that the result we had hoped for is false and to turn our attention to something else. But this reaction is a mistake, as it is in many other mathematical contexts, because there was something importantly correct about the idea that it was impossible to get rid of the fixed points of a rotation. It turns out that if you start with a rotation and try to get rid of the fixed points by continuously deforming it, then you are doomed to failure. In fact, in a certain sense there will always be exactly two fixed points. More generally, if you take any continuous function from S2 to S2 and continuously deform it, then you cannot change the number of fixed points.
Of course, these last two statements are patently false if taken at face value so some reinterpretation is needed. First, we must assume that the number of fixed points is finite, but this is not a huge assumption as it can be shown that a typical small perturbation of any continuous function will have only finitely many fixed points. Second, we must count the fixed points with appropriate weights. To define these, suppose that f(x) = x, and imagine a point y(t) that goes around x in a tiny circle as t goes from 0 to 1. We define the index of the fixed point x to be the number of turns made by the vector from y(t) to f (y (t)), counting this negatively if these turns are in the opposite direction to the way that y(t) goes around x. (This definition is problematic if f(y(t)) = y(t) for some t, but again we can make small perturbations and assume that this does not happen.) Then the sum of the indices of all the fixed points is the quantity that does not change if you continuously deform f.
It follows that if you continuously deform a rotation, then the sum of the indices will always be 2. From this it follows that there must be at least one fixed point. It also follows that you cannot continuously deform a rotation so that it becomes the map that sends each x to -x.
The notion of the index of a fixed point can be generalized in a fairly straightforward way to higher dimensions (using the concept of degree mentioned earlier), and one can show under very general circumstances that the sum of the indices of fixed points remains constant when you continuously deform a continuous map. This implies Brouwer’s fixed point theorem as follows. We can continuously deform any continuous map f : Bn → Bn into any other continuous map g : Bn → Bn by defining ft(x) = (1 - t)f(x) + tg(x) and letting t vary from 0 to 1. Let us therefore take g to be the map x ↦  x, which has a single fixed point. This fixed point has index 1 (as one can see easily in the two- dimensional case), and therefore the sum of the indices of the fixed points of f is 1 as well.
x, which has a single fixed point. This fixed point has index 1 (as one can see easily in the two- dimensional case), and therefore the sum of the indices of the fixed points of f is 1 as well.
In general, the sum of the indices of the fixed points of a function f defined on a suitable topological space X (such as a smooth compact MANIFOLD [I.3 §6.9]) can be calculated in terms of the effect of f on the homology groups of X. The resulting theorem is (a slight generalization of) the Lefschetz fixed point theorem.
The fact that the index of a continuous map is an invariant of continuous deformations can be used to give a proof of THE FUNDAMENTAL THEOREM OF ALGEBRA [V.13]. Consider, for instance, the problem of proving that the polynomial x5 + 3x + 8 has a root. This is the same as asking for a fixed point of the function x5 + 4x + 8, since if this equals x then x5 + 3x + 8 = 0. Now if we regard the polynomial x5 as being defined on the RIEMANN SPHERE [IV.14 §2.4] ℂ ∪ {∞}, then it has two fixed points, at 0 and ∞. Moreover, their indices are both 5 (since if x goes around 0 or ∞ in a “small circle,” then x5 goes around five times). Now the polynomials x5 + (4x + 8)t give us a continuous deformation from x5 to x5 + 4x + 8, and x5 + 4x + 8 has a fixed point of index 5 at ∞. It follows that there must be other fixed points, with indices adding up to 5. These are the roots of x5 + 3x + 8, and the indices are the multiplicities of the roots.
4 Infinite-Dimensional Fixed Point Theorems and Applications to Analysis
What happens if we try to generalize the Brouwer fixed point theorem to continuous maps defined on infinite-dimensional closed balls? The answer is that we will not be able to, as the following example shows. Let B be the set of all sequences (a1, a2, . . .) such that ∑n|an|2 ≤ 1. This is our closed ball; it is the unit ball of the HILBERT SPACE [III.37] 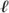 2. Given an infinite sequence a = (a1, a2, . . .), we write ||a|| for its norm (∑n|an|2)1/2. Now consider the map f: (a1, a2,. . .) ↦((1 – ||a||2)1/2, a1, a2,. . .). It is easy to check that f is continuous and that ||f (a) || = 1 for every a. Therefore, if a is a fixed point, we must have ||a|| = 1, from which we can see that a1 = 0. From this it follows that a2 = 0, and then that a3 = 0, and so on. In other words, a = 0. But this contradicts the condition that ||a|| = 1. Therefore, the map f has no fixed point.
2. Given an infinite sequence a = (a1, a2, . . .), we write ||a|| for its norm (∑n|an|2)1/2. Now consider the map f: (a1, a2,. . .) ↦((1 – ||a||2)1/2, a1, a2,. . .). It is easy to check that f is continuous and that ||f (a) || = 1 for every a. Therefore, if a is a fixed point, we must have ||a|| = 1, from which we can see that a1 = 0. From this it follows that a2 = 0, and then that a3 = 0, and so on. In other words, a = 0. But this contradicts the condition that ||a|| = 1. Therefore, the map f has no fixed point.
However, if we place extra conditions on a continuous map, then it is sometimes possible to prove fixed point theorems, and some of these theorems have important applications, notably to establishing the existence of solutions to differential equations.
An easy result of this type is the contraction mapping theorem. This states that if X is a METRIC SPACE [III.56] with a property known as completeness (which is briefly discussed in NORMED SPACES AND BANACH SPACES [III.62]) and f is a map from X to X such that there exists a constant ρ < 1 such that d (f (x), f(y)) ≤ ρd(x, y) for every x and y in X, then f must have a fixed point. To prove this, one picks any point x ∈ X and looks at the iterates x, f (x), f (f (x)), f (f (f (x))), and so on. Denoting these by x0, x1, x2, . . ., one can prove quite easily that d(xn, xm) tends to 0 as m and n both tend to infinity, and the completeness property then guarantees that the sequence (xn) has a limit. It is not hard to prove that this limit is a fixed point of f.
A more sophisticated example is the Schauder fixed point theorem, which states that if X is a Banach space, K is a COMPACT [III.9] convex subset of X, and f is a continuous function from K to K, then f has a fixed point. Roughly speaking, to prove this one approximates K by larger and larger finite-dimensional sets Kn and approximates f by continuous maps fn that take Kn to Kn. Brouwer’s fixed point theorem gives a sequence (xn such that fn(xn) = xn for each n. The compactness of K implies that the sequence (xn) has a convergent subsequence: its limit can be shown to be a fixed point of f.
The importance of these two theorems, and others of a similar nature, lies more in their applications than in their basic statements. A typical application is a proof that the differential equation
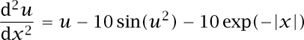
has a solution u such that u(x) is defined for every real number x and tends to 0 as x tends to ± ∞. We can rewrite this equation as
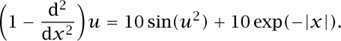
If we write the left-hand side as L(u), then this equation can be further rewritten as
u = L–1(10 sin (u2) + 10exp(–|x|)).
(It is possible to identify the operator L–1 explicitly.) If we now let X be the Banach space of continuous functions defined on ℝ that tend to 0 at ± ∞, with the uniform norm, then it can be shown that the right-hand side of this last equation defines a continuous function from X to a compact convex subset of X. Therefore, by the Schauder fixed point theorem, this highly nonlinear equation has a solution with the given boundary conditions, a result that is hard to prove in any other way.
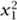 + · · · +
+ · · · + 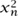 ≤ 1) and f is a continuous function from Bn to Bn, then f must have a fixed point. The set Bn is an n-dimensional solid sphere, but all that matters is its topological character, so we could take it to be another shape such as an n-dimensional cube or simplex.
≤ 1) and f is a continuous function from Bn to Bn, then f must have a fixed point. The set Bn is an n-dimensional solid sphere, but all that matters is its topological character, so we could take it to be another shape such as an n-dimensional cube or simplex.
 h is the identity on ∂D. (We let h be the map that takes a point of ∂D to itself and we let g be the continuous retraction.) Now continuous maps between topological spaces give rise to HOMOMORPHISMS [I.3 §4.1] between their homology groups, in such a way that compositions go to compositions and identity maps go to identity maps. (That is, there is a FUNCTOR [III.8] from the CATEGORY [III.8] of topological spaces and continuous maps to the category of groups and group homomorphisms.) This means that there must be homomorphisms ϕ: ℤ → {0} and ψ : {0} → ℤsuch that ψ
h is the identity on ∂D. (We let h be the map that takes a point of ∂D to itself and we let g be the continuous retraction.) Now continuous maps between topological spaces give rise to HOMOMORPHISMS [I.3 §4.1] between their homology groups, in such a way that compositions go to compositions and identity maps go to identity maps. (That is, there is a FUNCTOR [III.8] from the CATEGORY [III.8] of topological spaces and continuous maps to the category of groups and group homomorphisms.) This means that there must be homomorphisms ϕ: ℤ → {0} and ψ : {0} → ℤsuch that ψ  x, which has a single fixed point. This fixed point has index 1 (as one can see easily in the two- dimensional case), and therefore the sum of the indices of the fixed points of f is 1 as well.
x, which has a single fixed point. This fixed point has index 1 (as one can see easily in the two- dimensional case), and therefore the sum of the indices of the fixed points of f is 1 as well. 2. Given an infinite sequence a = (a1, a2, . . .), we write ||a|| for its norm (∑n|an|2)1/2. Now consider the map f: (a1, a2,. . .) ↦((1 – ||a||2)1/2, a1, a2,. . .). It is easy to check that f is continuous and that ||f (a) || = 1 for every a. Therefore, if a is a fixed point, we must have ||a|| = 1, from which we can see that a1 = 0. From this it follows that a2 = 0, and then that a3 = 0, and so on. In other words, a = 0. But this contradicts the condition that ||a|| = 1. Therefore, the map f has no fixed point.
2. Given an infinite sequence a = (a1, a2, . . .), we write ||a|| for its norm (∑n|an|2)1/2. Now consider the map f: (a1, a2,. . .) ↦((1 – ||a||2)1/2, a1, a2,. . .). It is easy to check that f is continuous and that ||f (a) || = 1 for every a. Therefore, if a is a fixed point, we must have ||a|| = 1, from which we can see that a1 = 0. From this it follows that a2 = 0, and then that a3 = 0, and so on. In other words, a = 0. But this contradicts the condition that ||a|| = 1. Therefore, the map f has no fixed point.