V.22 Liouville’s Theorem and Roth’s Theorem
One of the most famous theorems in mathematics is the statement that  is irrational. This means that there is no pair of integers p and q such that
is irrational. This means that there is no pair of integers p and q such that  = p/q, or equivalently that the equation p2 = 2q2 has no integer solutions apart from the trivial solution p = q = 0. The argument that proves this can be considerably generalized, and, in fact, if P(x) is any polynomial with integer coefficients and leading coefficient 1, then all its roots are either integers or irrational numbers. For example, since x3 + x - 1 is negative when x = 0 and positive when x = 1 it must have a root strictly between 0 and 1. This root is not an integer, so it must be irrational.
= p/q, or equivalently that the equation p2 = 2q2 has no integer solutions apart from the trivial solution p = q = 0. The argument that proves this can be considerably generalized, and, in fact, if P(x) is any polynomial with integer coefficients and leading coefficient 1, then all its roots are either integers or irrational numbers. For example, since x3 + x - 1 is negative when x = 0 and positive when x = 1 it must have a root strictly between 0 and 1. This root is not an integer, so it must be irrational.
Once one has proved that a number is irrational, it may seem as though not much more can be said. However, this is very far from true: given an irrational number, one can ask how close it is to being rational, and fascinating and extremely difficult questions arise as soon as one does so.
It is not immediately obvious what this question means, since every irrational number can be approximated as closely as you like by rational numbers. For example, the decimal expansion of  begins 1.414213. . . , which tells us that
begins 1.414213. . . , which tells us that  is within 1/100 000 of the rational number 141 421/100 000. More generally, for any positive integer q we can let p be the largest integer such that p/q <
is within 1/100 000 of the rational number 141 421/100 000. More generally, for any positive integer q we can let p be the largest integer such that p/q <  , and then p/q will be within 1/q of
, and then p/q will be within 1/q of  . In other words, if we want an approximation to
. In other words, if we want an approximation to  with accuracy 1/q, we can obtain it if we use a denominator of q.
with accuracy 1/q, we can obtain it if we use a denominator of q.
However, we can now ask the following question: are there denominators q for which one can one obtain an accuracy much better than 1/q? The answer turns out to be yes. To see this, let N be a positive integer and consider the numbers 0,  , 2
, 2 ,. . . , N
,. . . , N . Each of these can be written in the form m + α, where m is an integer and α, the fractional part, lies between 0 and 1. Since there are N + 1 numbers, at least two of their fractional parts must be within 1/N of each other. That is, we can find integers r < s between 0 and N such that if we write r
. Each of these can be written in the form m + α, where m is an integer and α, the fractional part, lies between 0 and 1. Since there are N + 1 numbers, at least two of their fractional parts must be within 1/N of each other. That is, we can find integers r < s between 0 and N such that if we write r = n+α and s
= n+α and s = m+β, then |α-β| ≤ 1/N. Thus, if we set
= m+β, then |α-β| ≤ 1/N. Thus, if we set 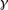 = α - β, we have (s - r) = n - m +
= α - β, we have (s - r) = n - m + 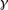 and |
and |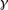 | ≤ 1/N. If we now let q = s - r and p n - m, then
| ≤ 1/N. If we now let q = s - r and p n - m, then  = p/q +
= p/q + 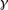 /q, so |
/q, so |  - p/q ≤ 1/qN. Since N ≥ q, 1/qN ≥ q, 1/q2, so for at least some positive integers q we can achieve an accuracy of 1/q2 using a denominator of q.
- p/q ≤ 1/qN. Since N ≥ q, 1/qN ≥ q, 1/q2, so for at least some positive integers q we can achieve an accuracy of 1/q2 using a denominator of q.
A different argument shows that we cannot do substantially better than this. Let p and q be any two positive integers. Since  is irrational, p2 and 2q2 are distinct positive integers, which implies that |p2 - 2q2| ≥ 1. On factorizing, we deduce that |p -
is irrational, p2 and 2q2 are distinct positive integers, which implies that |p2 - 2q2| ≥ 1. On factorizing, we deduce that |p -  | (p + q
| (p + q  ) ≥ 1. We can now divide through by q2 and obtain the inequality |p/q -
) ≥ 1. We can now divide through by q2 and obtain the inequality |p/q -  (p/q +
(p/q +  ) ≤ 1/q2. We may as well assume that p/q is less than 2, since otherwise it is not a good approximation to
) ≤ 1/q2. We may as well assume that p/q is less than 2, since otherwise it is not a good approximation to  . But then p/q +
. But then p/q +  is less than 4, so the inequality implies that p/q -
is less than 4, so the inequality implies that p/q -  ≤ 1/4q2. Thus, with a denominator of q we cannot achieve an accuracy better than 1/4q2.
≤ 1/4q2. Thus, with a denominator of q we cannot achieve an accuracy better than 1/4q2.
A generalization of this argument proves Liouville’s theorem: if x is an irrational root of a polynomial of degree d and p and q are integers, then |p/q - x| cannot be substantially smaller than 1/qd. When x =  this reduces to what we have just shown, since then x2 - 2 = 0 and we can set d = 2. However, from Liouville’s theorem we know many similar facts, such as that |p/q -
this reduces to what we have just shown, since then x2 - 2 = 0 and we can set d = 2. However, from Liouville’s theorem we know many similar facts, such as that |p/q - 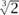 | cannot be substantially smaller than 1/q3.
| cannot be substantially smaller than 1/q3.
Roth’s theorem, proved in 1955, is the astonishing assertion that the power d that appears in Liouville’s theorem can be improved—almost as far as 2. To be precise, given any irrational root x of any polynomial, and any number r > 2, there is a constant c > 0 with the property that |p/q - x| is always at least as big as c/qr. (The proof gives no information whatsoever about c beyond the fact that it is positive. It is a major open problem to understand something about how c depends on r and x.)
To see why this is a much deeper result than Liouville’s theorem, consider the example of 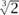 . Underlying the proof that |p/q -
. Underlying the proof that |p/q - 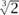 | is never much smaller than 1/q3 is the simple fact that p3 and 2q3 are distinct integers and therefore differ by at least 1. In order to prove a substantially better result such as Roth’s theorem, one must show much more: that p3 and 2q3 differ by an amount that grows as p and q grow. For example, if one wishes to prove Roth’s theorem when r =
| is never much smaller than 1/q3 is the simple fact that p3 and 2q3 are distinct integers and therefore differ by at least 1. In order to prove a substantially better result such as Roth’s theorem, one must show much more: that p3 and 2q3 differ by an amount that grows as p and q grow. For example, if one wishes to prove Roth’s theorem when r =  , it is necessary to show that p3 and 2q3 must always differ by an amount comparable to or greater than
, it is necessary to show that p3 and 2q3 must always differ by an amount comparable to or greater than 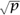 , and it is far from obvious why this should be so.
, and it is far from obvious why this should be so.
The Mordell Conjecture
See RATIONAL POINTS ON CURVES AND THE MQRDELL CONJECTURE [V.29]
 is irrational. This means that there is no pair of integers p and q such that
is irrational. This means that there is no pair of integers p and q such that  = p/q, or equivalently that the equation p2 = 2q2 has no integer solutions apart from the trivial solution p = q = 0. The argument that proves this can be considerably generalized, and, in fact, if P(x) is any polynomial with integer coefficients and leading coefficient 1, then all its roots are either integers or irrational numbers. For example, since x3 + x - 1 is negative when x = 0 and positive when x = 1 it must have a root strictly between 0 and 1. This root is not an integer, so it must be irrational.
= p/q, or equivalently that the equation p2 = 2q2 has no integer solutions apart from the trivial solution p = q = 0. The argument that proves this can be considerably generalized, and, in fact, if P(x) is any polynomial with integer coefficients and leading coefficient 1, then all its roots are either integers or irrational numbers. For example, since x3 + x - 1 is negative when x = 0 and positive when x = 1 it must have a root strictly between 0 and 1. This root is not an integer, so it must be irrational.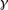 = α - β, we have (s - r) = n - m +
= α - β, we have (s - r) = n - m + 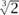 | cannot be substantially smaller than 1/q3.
| cannot be substantially smaller than 1/q3. , it is necessary to show that p3 and 2q3 must always differ by an amount comparable to or greater than
, it is necessary to show that p3 and 2q3 must always differ by an amount comparable to or greater than 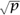 , and it is far from obvious why this should be so.
, and it is far from obvious why this should be so.