V.23 Mostow’s Strong Rigidity Theorem
David Fisher
1 What Are Rigidity Theorems?
A typical rigidity theorem is a statement that some class of objects is much smaller than one might expect. To make this notion clear, let us look at some examples of MODULI SPACES [IV.8] that might lead us to expect that spaces of a certain type would in general be large.
2 Some Moduli Spaces
A flat metric on an n-dimensional MANIFOLD [I.3 §6.9] is a METRIC [III.56] that is locally isometric to the usual metric on the Euclidean space ℝn. In other words, every point x in the manifold is contained in a neighborhood Nx such that there is a distance-preserving bijection from Nx to a subset of ℝn. For our first example, we shall consider flat metrics on a torus. We shall consider just the two-dimensional torus, but the phenomena we shall discuss occur in higher dimensions as well.
The simplest way of putting a flat metric on the two-dimensional torus 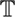 2 is to view it as the QUOTIENT [I.3 §3.3] of ℝ2 by a discrete subgroup, or lattice, that is isomorphic to ℤ2. In fact, it is not too hard to see that every flat metric arises in essentially this way. However, there is a choice involved: the choice of which lattice to take. An obvious choice is ℤ2 itself. But one can also take any invertible linear transformation A, apply it to ℤ2, and then define the torus as ℝ2/A(ℤ2), which gives rise to another metric. A natural question to ask is, when do two choices of A give rise to the same metric? Usually, one studies only the cases when the DETERMINANT [III.15] of A is 1, since it is easy to deduce from these what happens in general. The group of all such linear maps is called SL2 ( ℝ).
2 is to view it as the QUOTIENT [I.3 §3.3] of ℝ2 by a discrete subgroup, or lattice, that is isomorphic to ℤ2. In fact, it is not too hard to see that every flat metric arises in essentially this way. However, there is a choice involved: the choice of which lattice to take. An obvious choice is ℤ2 itself. But one can also take any invertible linear transformation A, apply it to ℤ2, and then define the torus as ℝ2/A(ℤ2), which gives rise to another metric. A natural question to ask is, when do two choices of A give rise to the same metric? Usually, one studies only the cases when the DETERMINANT [III.15] of A is 1, since it is easy to deduce from these what happens in general. The group of all such linear maps is called SL2 ( ℝ).
If A is orthogonal, then it just rotates the lattice ℤ2 and therefore A(ℤ2) gives rise to the same metric as ℤ2. What is slightly less obvious is that there are other maps A that give rise to this metric as well, namely all maps of determinant 1 whose matrices with respect to the standard basis of ℝ2 have integer entries. The group of all these maps is called SL2 (ℤ). If A belongs to SL2 (ℤ), then the reason that A (ℤ2) gives rise to the same metric as ℤ2 is simple: A(ℤ2) is actually equal to ℤ2.
Loosely speaking, what we have just done is identify the space of flat metrics on 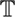 2 with the set SL2 (ℤ) \ SL2 ( ℝ) / S0(2). (This is notation for the set SL2 ( ℝ), with two maps A and B considered equivalent if B can be expressed as A multiplied by a product of matrices from SO(2) and SL2 (ℤ).) In higher dimensions, a similar discussion shows that one can identify the space of flat metrics on the n-dimensional torus
2 with the set SL2 (ℤ) \ SL2 ( ℝ) / S0(2). (This is notation for the set SL2 ( ℝ), with two maps A and B considered equivalent if B can be expressed as A multiplied by a product of matrices from SO(2) and SL2 (ℤ).) In higher dimensions, a similar discussion shows that one can identify the space of flat metrics on the n-dimensional torus 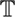 n with SLn (ℤ) \ SLn ( ℝ) / SO(n).
n with SLn (ℤ) \ SLn ( ℝ) / SO(n).
Returning to two dimensions, a torus is a surface of genus 1 (since it has one “hole”). A similar construction gives rise to a moduli space of metrics on a surface of higher genus, but now the metrics will be hyperbolic rather than flat. The UNIFORMIZATION THEOREM [V.34] says that any compact connected surface admits a metric of constant CURVATURE [III.13]: when the genus is 2 or more, this curvature must be negative, which implies that the surface is a QUOTIENT [I.3 §3.3] Of the HYPERBOLIC PLANE [I.3 §6.6]  2 by a group Γ that acts on
2 by a group Γ that acts on  2 as a set of isometrics. (See FUCHSIAN GROUPS [III.28].)
2 as a set of isometrics. (See FUCHSIAN GROUPS [III.28].)
Conversely, if we want to construct a metric of constant curvature on a surface of higher genus, we can take a subgroup Γ of the group of isometrics of  2 (which is isomorphic to SL2 ( ℝ)) and we can consider the quotient
2 (which is isomorphic to SL2 ( ℝ)) and we can consider the quotient  2/Γ, which is analogous to the quotient ℝ2/ℤ2 that we considered earlier. If Γ has no elements of finite order and if for each x the orbit of x (the set of images of x under the isometrics in Γ) is a discrete subset of
2/Γ, which is analogous to the quotient ℝ2/ℤ2 that we considered earlier. If Γ has no elements of finite order and if for each x the orbit of x (the set of images of x under the isometrics in Γ) is a discrete subset of  2, then this space is a manifold. Furthermore, if there is a compact region in
2, then this space is a manifold. Furthermore, if there is a compact region in  2, called a fundamental domain, whose translates cover
2, called a fundamental domain, whose translates cover  2, then the manifold is compact. There are two fairly simple ways to construct examples of groups Γ with these properties: one is to use reflection groups and the other is to use a bit of number theory.
2, then the manifold is compact. There are two fairly simple ways to construct examples of groups Γ with these properties: one is to use reflection groups and the other is to use a bit of number theory.
Now we can ask the same question for these metrics. In other words, given a surface S of genus at least 2, how many hyperbolic metrics can we find on S? The answer is quite similar to the answer for 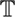 2. For instance, if the genus is 2, then there is a connected six-dimensional space of such structures. This is a bit more difficult to see, as the space is not constructed in any simple way from a LIE GROUP [III.48 §1] (such as SLn( ℝ)) and its subgroups. We will not describe this construction here but it can be found in Thurston (1997) or in MODULI SPACES [IV.8].
2. For instance, if the genus is 2, then there is a connected six-dimensional space of such structures. This is a bit more difficult to see, as the space is not constructed in any simple way from a LIE GROUP [III.48 §1] (such as SLn( ℝ)) and its subgroups. We will not describe this construction here but it can be found in Thurston (1997) or in MODULI SPACES [IV.8].
3 Mostow’s Theorem
Thinking about the last two sets of examples leads to a natural question: what about compact three-dimensional hyperbolic manifolds? Or n-dimensional ones? To be clear, a compact n-dimensional hyperbolic manifold is the quotient of  n by a discrete group Γ of isometrics of the hyperbolic n-space
n by a discrete group Γ of isometrics of the hyperbolic n-space  n such that Γ has no elements of finite order and there is a compact fundamental domain for Γ. Given this description, the reader may wonder if there are any such groups Γ. Once again, there are two easy ways of constructing them, one using a bit of number theory and another using reflection groups. (However, slightly surprisingly, the method using reflection groups works only in fairly small dimensions.) The constructions are all a bit technical so we will not go through them here. There are also many other examples of compact hyperbolic manifolds, particularly in three dimensions, where “most” manifolds are hyperbolic by the GEOMETRIZATION THEOREM [IV.7 §2.4].
n such that Γ has no elements of finite order and there is a compact fundamental domain for Γ. Given this description, the reader may wonder if there are any such groups Γ. Once again, there are two easy ways of constructing them, one using a bit of number theory and another using reflection groups. (However, slightly surprisingly, the method using reflection groups works only in fairly small dimensions.) The constructions are all a bit technical so we will not go through them here. There are also many other examples of compact hyperbolic manifolds, particularly in three dimensions, where “most” manifolds are hyperbolic by the GEOMETRIZATION THEOREM [IV.7 §2.4].
Here we shall concentrate less on the existence of hyperbolic manifolds and more on the question that has been our principal concern in this article: if X is a manifold that can be represented in the form  n/Γ, then how many ways are there of giving X this structure? This question is equivalent to asking how many injective homomorphisms there are from Γ to the group of all isometrics of
n/Γ, then how many ways are there of giving X this structure? This question is equivalent to asking how many injective homomorphisms there are from Γ to the group of all isometrics of  n such that the image of Γ is discrete and cocompact. (A subset X of a group G is cocompact if there is a compact subset K of G such that XK = G. For instance, ℤ2 is a cocompact subset of ℝ2 because ℝ2 = ℤ2 + [0,1]2 and the closed unit square [0, 1]2 is compact.) As we have seen, when n = 2 there is a continuum of such homomorphisms, and the same is true in all dimensions if we replace
n such that the image of Γ is discrete and cocompact. (A subset X of a group G is cocompact if there is a compact subset K of G such that XK = G. For instance, ℤ2 is a cocompact subset of ℝ2 because ℝ2 = ℤ2 + [0,1]2 and the closed unit square [0, 1]2 is compact.) As we have seen, when n = 2 there is a continuum of such homomorphisms, and the same is true in all dimensions if we replace  n by ℝn. So it is rather surprising that when n ≥ 3, the answer for
n by ℝn. So it is rather surprising that when n ≥ 3, the answer for  n is exactly 1. This is a special case of Mostow’s rigidity theorem.
n is exactly 1. This is a special case of Mostow’s rigidity theorem.
What does this result mean? Suppose we know that a manifold M is a quotient of  n by some discrete cocompact group of isometrics. The topology of M completely determines the group Γ up to isomorphism: it is just the FUNDAMENTAL GROUP [IV.6 §2] Of M. The result we have just stated tells us that this purely topological information about the manifold M completely determines the geometry of
n by some discrete cocompact group of isometrics. The topology of M completely determines the group Γ up to isomorphism: it is just the FUNDAMENTAL GROUP [IV.6 §2] Of M. The result we have just stated tells us that this purely topological information about the manifold M completely determines the geometry of  n/Γ (that is, its structure as a metric space). More precisely, it says that any homeomorphism, or even homotopy equivalence, from M to another hyperbolic manifold N is homotopic to an isometry. In other words, any purely topological equivalence can be realized as a geometric equivalence.
n/Γ (that is, its structure as a metric space). More precisely, it says that any homeomorphism, or even homotopy equivalence, from M to another hyperbolic manifold N is homotopic to an isometry. In other words, any purely topological equivalence can be realized as a geometric equivalence.
The full Mostow rigidity theorem concerns objects called compact locally symmetric manifolds. Given a manifold with a metric, we say that it is locally symmetric if the central symmetry at every point is a local isometry. The central symmetry at a point m is defined formally as multiplication by -1 in the tangent space to m: one can picture it as taking a very small neighborhood of m and “reflecting through m.” It turns out that every locally symmetric space is a quotient of a symmetric space: that is, a space such that the central symmetry at every point is a global isometry. Clearly, symmetric spaces have very large isometry groups. The work of CARTAN [VI.69] shows that the resulting isometry groups are exactly the semisimple LIE GROUPS [III.48 §1]. We will not say precisely what these are, but they include the classical matrix groups such as SLn( ℝ), SLn(ℂ), and Spn( ℝ). Other examples, which can also be realized as matrix groups, include the isometry groups of complex and quaternionic hyperbolic spaces.
In general, given a Lie group G and a discrete subgroup Γ, we say that Γ is a cocompact lattice if there is a compact fundamental domain for Γ in G. Cartan’s theorem has the consequence that any compact locally symmetric space is a quotient Γ\G/K, where G is the isometry group of the universal cover and K is the (necessarily compact) set of isometrics that fix a specified point. Mostow’s theorem says the same here as it said for  n/Γ: given such a manifold, there is only one way to realize it as Γ\G/K. Or, equivalently, any homeomorphism between two such manifolds is always homotopic to an isometry unless the relevant locally symmetric space is a product of a flat torus or a hyperbolic surface with some other locally symmetric manifold.
n/Γ: given such a manifold, there is only one way to realize it as Γ\G/K. Or, equivalently, any homeomorphism between two such manifolds is always homotopic to an isometry unless the relevant locally symmetric space is a product of a flat torus or a hyperbolic surface with some other locally symmetric manifold.
One might well ask how Mostow discovered such a phenomenon. His work certainly did not occur in a vacuum. In fact, earlier work of Calabi, Selberg, Vesentini, and WEIL [VI.93] had already shown that the moduli spaces Mostow was studying were discrete: in other words, unlike flat tori or two-dimensional hyperbolic manifolds, higher-dimensional locally symmetric spaces could admit only a discrete set of locally symmetric metrics. Mostow has said explicitly that he was motivated by the desire to find a more geometric understanding of this fact.
Another point worth making is that Mostow’s proof is at least as surprising as his theorem. At the time, the study of locally symmetric spaces, or equivalently of semisimple Lie groups and their lattices, was dominated by two sets of techniques: one set that was purely algebraic and another that used classical methods in differential geometry. Mostow’s original proof (which was only for  [n) uses instead the theory of quasi-conformal mappings and some ideas from dynamics. Raghunathan, another leading figure in the field, has said that when he first read Mostow’s paper, he thought it must be by a different man named Mostow. Similar uses of surprising dynamical and analytical ideas to study the same objects occurred almost simultaneously in work of Furstenberg and Margulis. These ideas have had a long and interesting legacy in the study of locally symmetric spaces, semisimple Lie groups, and related objects.
[n) uses instead the theory of quasi-conformal mappings and some ideas from dynamics. Raghunathan, another leading figure in the field, has said that when he first read Mostow’s paper, he thought it must be by a different man named Mostow. Similar uses of surprising dynamical and analytical ideas to study the same objects occurred almost simultaneously in work of Furstenberg and Margulis. These ideas have had a long and interesting legacy in the study of locally symmetric spaces, semisimple Lie groups, and related objects.
Further Reading
Furstenberg, H. 1971. Boundaries of Lie groups and discrete subgroups. In Actes du Congrès International des Mathématiciens, Nice, 1970, volume 2, pp. 301–6. Paris: Gauthier-Villars.
Margulis, G. A. 1977. Discrete groups of motions of manifolds of non-positive curvature. In Proceedings of the International Congress of Mathematicians, Vancouver, 1974, pp. 33–45. AMS Translations, volume 109. Providence, RI: American Mathematical Society.
Mostow, G. D. 1973. Strong Rigidity of Locally Symmetric Spaces. Annals of Mathematics Studies, number 78. Princeton, NJ: Princeton University Press.
Thurston, W. P. 1997. Three-Dimensional Geometry and Topology, edited by S. Levy, volume 1. Princeton Mathematical Series, number 35. Princeton, NJ: Princeton University Press.
 2 is to view it as the QUOTIENT [I.3 §3.3] of ℝ2 by a discrete subgroup, or lattice, that is isomorphic to ℤ2. In fact, it is not too hard to see that every flat metric arises in essentially this way. However, there is a choice involved: the choice of which lattice to take. An obvious choice is ℤ2 itself. But one can also take any invertible linear transformation A, apply it to ℤ2, and then define the torus as ℝ2/A(ℤ2), which gives rise to another metric. A natural question to ask is, when do two choices of A give rise to the same metric? Usually, one studies only the cases when the DETERMINANT [III.15] of A is 1, since it is easy to deduce from these what happens in general. The group of all such linear maps is called SL2 ( ℝ).
2 is to view it as the QUOTIENT [I.3 §3.3] of ℝ2 by a discrete subgroup, or lattice, that is isomorphic to ℤ2. In fact, it is not too hard to see that every flat metric arises in essentially this way. However, there is a choice involved: the choice of which lattice to take. An obvious choice is ℤ2 itself. But one can also take any invertible linear transformation A, apply it to ℤ2, and then define the torus as ℝ2/A(ℤ2), which gives rise to another metric. A natural question to ask is, when do two choices of A give rise to the same metric? Usually, one studies only the cases when the DETERMINANT [III.15] of A is 1, since it is easy to deduce from these what happens in general. The group of all such linear maps is called SL2 ( ℝ). 2 by a group Γ that acts on
2 by a group Γ that acts on