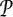 versus
versus 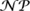 Problem
Problem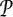 versus
versus 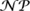 Problem
ProblemThe 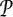 versus
versus 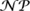 problem is widely considered to be the most important unsolved problem in theoretical computer science, and one of the most important in all of mathematics.
problem is widely considered to be the most important unsolved problem in theoretical computer science, and one of the most important in all of mathematics. 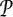 and
and 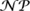 are two of the most basic COMPUTATIONAL COMPLEXITY CLASSES [III.10]:
are two of the most basic COMPUTATIONAL COMPLEXITY CLASSES [III.10]: 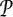 is the class of all computational tasks that can be performed in a time that is polynomial in the length of the input, and
is the class of all computational tasks that can be performed in a time that is polynomial in the length of the input, and 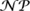 is the class of all computational tasks where a correct answer can be verified in a time that is polynomial in the length of the input. An example of the former is multiplying two n-digit integers (which, even if you use long multiplication, takes roughly n2 arithmetical operations). An example of the latter is searching in a GRAPH [III.34] with n vertices for a set of m vertices, any two of which are joined by an edge: if you are presented with m such vertices, then you just have to check the (
is the class of all computational tasks where a correct answer can be verified in a time that is polynomial in the length of the input. An example of the former is multiplying two n-digit integers (which, even if you use long multiplication, takes roughly n2 arithmetical operations). An example of the latter is searching in a GRAPH [III.34] with n vertices for a set of m vertices, any two of which are joined by an edge: if you are presented with m such vertices, then you just have to check the (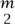 ) pairs of those vertices to make sure that each pair is indeed an edge of the graph.
) pairs of those vertices to make sure that each pair is indeed an edge of the graph.
It appears to be much harder to find m vertices that are all joined than to check that a given m vertices are all joined. This suggests that problems in 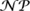 are in general harder than problems in
are in general harder than problems in 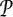 . The
. The 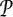 versus
versus 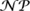 problem asks for a proof that the complexity classes
problem asks for a proof that the complexity classes 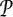 and
and 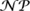 really are distinct. For a detailed discussion of the problem, see COMPUTATIONAL COMPLEXITY [IV.20].
really are distinct. For a detailed discussion of the problem, see COMPUTATIONAL COMPLEXITY [IV.20].