V.31 The Riemann-Roch Theorem
A RIEMANN SURFACE [III.79] is a MANIFOLD [I.3 §6.9] that “looks locally like  ,” in the usual sense of this sort of phrase. In other words, every point has a neighborhood that can be mapped bijectively to an open subset of
,” in the usual sense of this sort of phrase. In other words, every point has a neighborhood that can be mapped bijectively to an open subset of  , and where two such neighborhoods overlap, the “transition functions” are HOLOMORPHIC [I.3 §5.6]. One can think of a Riemann surface as the most general sort of set on which the notion of a holomorphic function (that is, a complex-differentiable function) of one complex variable makes sense.
, and where two such neighborhoods overlap, the “transition functions” are HOLOMORPHIC [I.3 §5.6]. One can think of a Riemann surface as the most general sort of set on which the notion of a holomorphic function (that is, a complex-differentiable function) of one complex variable makes sense.
The definition of differentiability is a local one: a function is differentiable if and only if a certain condition holds at each point z, and the condition at z depends only on the behavior of f at points very close to z. However, one of the surprises of complex analysis is that holomorphic functions are much more global than their basic definition would lead one to expect. Indeed, if you know the values of a holomorphic function f:  →
→  at every point in a small neighborhood of a single point z, then you can deduce its values at every point in
at every point in a small neighborhood of a single point z, then you can deduce its values at every point in  . And the same is true if you replace
. And the same is true if you replace  by any other (connected) Riemann surface.
by any other (connected) Riemann surface.
Here is a second illustration of the global nature of holomorphic functions. One of the most basic Riemann surfaces is the so-called Riemann sphere 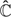 , which is obtained from
, which is obtained from  by adding a “point at infinity.” A function f:
by adding a “point at infinity.” A function f: 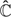 →
→  is said to be holomorphic if the following conditions hold:
is said to be holomorphic if the following conditions hold:
- f is differentiable at every point of
 ;
;
- f (z) tends to a limit w as z → ∞ in any direction;
- w is the value of f at ∞.
What, then, are the holomorphic functions from 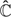 to
to  ? A holomorphic function f is continuous, from which it follows that if f (z) tends to a limit as z → ∞, then f is bounded on
? A holomorphic function f is continuous, from which it follows that if f (z) tends to a limit as z → ∞, then f is bounded on  . But a well-known theorem of LIOUVILLE [VI.39] states that a bounded holomorphic function defined on all of
. But a well-known theorem of LIOUVILLE [VI.39] states that a bounded holomorphic function defined on all of  must be constant. So the only holomorphic functions from
must be constant. So the only holomorphic functions from 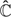 to
to  are constant!
are constant!
One might take the attitude that it was slightly artificial to consider maps from 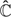 to
to  . Why not look at maps from
. Why not look at maps from 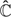 to
to  ? Such maps are equivalent to functions from
? Such maps are equivalent to functions from  to
to  that are allowed to tend to infinity at a finite set of points z1, . . . ,zk, called poles, and must tend to a limit as z → ∞. (This limit is allowed to be the point ∞. We say that f (z) → ∞ as z → ∞ if we can make |f (z)| arbitrarily large by making |z| large enough. Note that some familiar functions such as eZ are ruled out since it is possible for |z| to be large and ez to be small.) Functions with this property are called meromorphic. A typical example is z, or z2, or (1 + z) / (1 - z), or indeed any rational function in z; it can in fact be shown that any meromorphic function from
that are allowed to tend to infinity at a finite set of points z1, . . . ,zk, called poles, and must tend to a limit as z → ∞. (This limit is allowed to be the point ∞. We say that f (z) → ∞ as z → ∞ if we can make |f (z)| arbitrarily large by making |z| large enough. Note that some familiar functions such as eZ are ruled out since it is possible for |z| to be large and ez to be small.) Functions with this property are called meromorphic. A typical example is z, or z2, or (1 + z) / (1 - z), or indeed any rational function in z; it can in fact be shown that any meromorphic function from 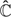 to
to 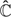 is rational.
is rational.
The notion of a meromorphic function also makes sense on other Riemann surfaces. One can think of it as a function that is holomorphic except at a set of isolated points where it tends to infinity (If the function is defined on  , there may be infinitely many such points, but a COMPACT [III.9] surface such as
, there may be infinitely many such points, but a COMPACT [III.9] surface such as  cannot contain infinitely many points that are all isolated from each other, so a meromorphic function on a compact surface has at most finitely many poles.)
cannot contain infinitely many points that are all isolated from each other, so a meromorphic function on a compact surface has at most finitely many poles.)
A particularly important example is when the Riemann surface in question is a torus. We can regard such a surface as the QUOTIENT [I.3 §3.3] of  by the lattice generated by two complex numbers u and v such that u / v is not real. There is then a one-to-one correspondence between functions defined on the torus and functions f defined on
by the lattice generated by two complex numbers u and v such that u / v is not real. There is then a one-to-one correspondence between functions defined on the torus and functions f defined on  that are doubly periodic, in the sense that f (z + u) and f (z + v) are both equal to f (z) for every z. Liouville’s theorem again implies that if such a function is holomorphic then it is constant; however, there are interesting examples of doubly periodic meromorphic functions. Such functions are called elliptic functions.
that are doubly periodic, in the sense that f (z + u) and f (z + v) are both equal to f (z) for every z. Liouville’s theorem again implies that if such a function is holomorphic then it is constant; however, there are interesting examples of doubly periodic meromorphic functions. Such functions are called elliptic functions.
Even here, the global nature, or “rigidity,” of holomorphic functions asserts itself, by greatly restricting the supply of elliptic functions. Indeed, one can define a single function, called the Weierstrass P-function ℘, with the property that any other elliptic function with respect to a given pair of generators u and v can be expressed as a rational function of ℘ and its derivative. Weierstrass’s function (for the generators u and v) is given by the formula
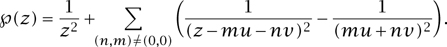
Notice that the double periodicity is built into the definition, and that ℘ has a pole at every point in the lattice generated by u and v. If we think of ℘ as a function on the torus, then it has just one pole. Near this pole, f tends to infinity at the same rate as the function 1/z2 does when z tends to 0; we say that the pole has order 2. More generally, if a function f tends to infinity at the same rate as 1 /zk, then the resulting pole has order k.
Suppose we take a compact Riemann surface S and choose from it a finite set of points z1, . . . , Zr. Given a sequence d1,. . . , dr of positive integers, can we find a meromorphic function f defined on S such that its poles are z1, . . . , zr and such that for each i the order of the pole at zi is at most di? The results mentioned so far would lead us to expect that this might be possible, but that there would probably not be a huge supply of such functions. Since a linear combination of such functions gives us another one, the set of functions we are interested in forms a VECTOR SPACE [I.3 §2.3], so we could hope to quantify “how many” functions there are by investigating the dimension of this space.
As we might by now expect, this dimension turns out to be finite. RIEMANN [VI.49] proved that if the poles are required to be simple (that is, di, = 1 for i = 1, 2, . . . r), then the dimension l is at least r - g + 1, where g is the GENUS [III.33] of the surface, which means, roughly speaking, the number of holes it has. This result is called Riemann’s inequality. Roch’s contribution was to interpret the difference between l and r - g + 1 as the dimension of another space of functions. This often makes it possible to calculate the dimension l exactly. For instance, under certain circumstances one can show that the dimension of the space of functions identified by Roch is 0, in which case l = r - g + 1. In particular, this is the case when r  2g - 1.
2g - 1.
The original question we asked was more general in that we did not require the poles to be simple: rather, we wanted the order of the pole at zi to be at most di. However, the result generalizes straightforwardly, and l is now at least d1 + . . . + dr - g + 1, with the differen again equal to the dimension of a certain space of functions that one can define. One can even ask for some of the di to be negative, interpreting a “pole of order at most di” to mean a zero of multiplicity at least -di.
The Riemann-Roch theorem is a basic tool for computing the dimensions of spaces of holomorphic or meromorphic functions on compact surfaces (which is often equivalent to requiring them to obey certain symmetry conditions). Let us begin with a very simple example. It is not hard to show that every meromorphic function defined on the Riemann sphere with at most simple poles at 0 and 1 has to take the form a + b / z + c / (z - 1). This is a three-dimensional space, and that is what the Riemann-Roch theorem predicts. A more sophisticated example concerns the Weierstrass P-function. We saw earlier that this is a doubly periodic meromorphic function defined on  with a pole of order 2 at each point in the lattice generated by u and v. The existence (and essential uniqueness) of such a function can be proved more abstractly with the help of the Riemann-Roch theorem: it shows that the space of such functions has dimension 2, so they can all be built out of a single function ℘ and the constant functions. Similarly, the theorem can be used to compute dimensions of spaces of MODULAR FORMS [III.59].
with a pole of order 2 at each point in the lattice generated by u and v. The existence (and essential uniqueness) of such a function can be proved more abstractly with the help of the Riemann-Roch theorem: it shows that the space of such functions has dimension 2, so they can all be built out of a single function ℘ and the constant functions. Similarly, the theorem can be used to compute dimensions of spaces of MODULAR FORMS [III.59].
The Riemann-Roch theorem has been reformulated and generalized many times, which has made it even more useful as a computational tool, and a central result in algebraic geometry: for example, Hirzebruch found a higher-dimensional generalization, which was generalized further by Grothendieck to a statement about advanced concepts in modern algebraic geometry such as SCHEMES [IV.5 §3] and “sheaves.” Hirzebruch′s generalization, like the classical result about curves, expresses an analytically defined quantity in terms of purely topological invariants: it is this feature of both results that underlies their importance. Another generalization of which the same can be said is the famous ATIYAH-SINGER INDEX THEOREM [V.2], which has itself been generalized several times.
 ,” in the usual sense of this sort of phrase. In other words, every point has a neighborhood that can be mapped bijectively to an open subset of
,” in the usual sense of this sort of phrase. In other words, every point has a neighborhood that can be mapped bijectively to an open subset of  , and where two such neighborhoods overlap, the “transition functions” are HOLOMORPHIC [I.3 §5.6]. One can think of a Riemann surface as the most general sort of set on which the notion of a holomorphic function (that is, a complex-differentiable function) of one complex variable makes sense.
, and where two such neighborhoods overlap, the “transition functions” are HOLOMORPHIC [I.3 §5.6]. One can think of a Riemann surface as the most general sort of set on which the notion of a holomorphic function (that is, a complex-differentiable function) of one complex variable makes sense. , which is obtained from
, which is obtained from 
 2g - 1.
2g - 1.