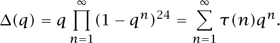
The Weil conjectures constitute one of the central landmarks of twentieth-century ALGEBRAIC GEOMETRY [IV.4]: not only was their proof a dramatic triumph, but they were the driving force behind a striking number of fundamental advances in the field. The conjectures treat a very elementary problem: how to count the number of solutions to systems of polynomial equations over finite FIELDS [I.3 §2.2]. While one might ultimately be more interested in solutions over, say, the field of rational numbers, the problem is far more tractable Over finite fields, and LOCAL–GLOBAL PRINCIPLES [III.51] such as THE BIRCH–SWINNERTON-DYER CONJECTURE [V.4] establish strong, albeit subtle, relationships between the two cases.
Moreover, there are some basic questions that have nonobvious connections to the Weil conjectures. The most famous of these is the Ramanujan conjecture, which concerns the coefficients of Δ(q), one of the most fundamental examples of a MODULAR FORM [III.59]. We obtain the function τ(n) from the formula for Δ(q) as follows:
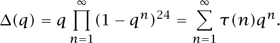
RAMANUJAN [VI.82] conjectured that |τ(p)| ≤ 2p11/2 for any prime number p. This is closely related to a statement on the number of ways of writing p as a sum of twenty-four squares. Work of Eichler, Shimura, Kuga, Ihara, and Deligne showed that in fact Ramanujan’s conjecture is a consequence of the Weil conjectures, so that Deligne’s proof of the latter in 1974 also resolved the former.
We begin with a brief historical summary of developments prior to WEIL [VI.93] and follow this with a more precise description of the statement of his conjectures. Finally, we sketch the ideas behind their proof.
Our story begins with the seminal work of RIEMANN [VI.49] on the classical ZETA FUNCTION [IV.2 §3], which we recall is defined by the sum
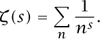
EULER [VI.19] had studied this function for real values of s, but Riemann, in his remarkable eight-page paper of 1859, went much further. He looked at complex values as well, and therefore had at his disposal the considerable resources of complex analysis. In particular, although the above sum for ζ(s) converges only for complex numbers s that have real part Re(s) strictly greater than 1, Riemann showed that the function itself can be extended to an analytic function defined on the entire complex plane, except at the point s = 1, at which it tends to infinity. He showed, moreover, that ζ(s) satisfies a certain functional equation relating ζ(s) to ζ(1 - s), which introduced an important kind of symmetry around the line Re(s) =  . Most famously (or infamously), he conjectured what is now known as the RIEMANN HYPOTHESIS [I.4 §3]: that, aside from easily analyzed “trivial zeros” on the negative real axis, every zero of ζ(s) occurs on the line Re(s) =
. Most famously (or infamously), he conjectured what is now known as the RIEMANN HYPOTHESIS [I.4 §3]: that, aside from easily analyzed “trivial zeros” on the negative real axis, every zero of ζ(s) occurs on the line Re(s) =  . Riemann’s motivation for studying ζ(s) was to analyze the distribution of prime numbers, but it fell to later authors (HADAMARD [VI.65], DE LA VALLÉE POUSSIN [VI.67], and Van Koch) to bring this vision to fruition. They used the zeta function to prove the PRIME NUMBER THEOREM [I.4 §3], which determined the asymptotic distribution of prime numbers, and also showed that the Riemann hypothesis is equivalent to a particularly strong upper bound for the error term in the prime number theorem.
. Riemann’s motivation for studying ζ(s) was to analyze the distribution of prime numbers, but it fell to later authors (HADAMARD [VI.65], DE LA VALLÉE POUSSIN [VI.67], and Van Koch) to bring this vision to fruition. They used the zeta function to prove the PRIME NUMBER THEOREM [I.4 §3], which determined the asymptotic distribution of prime numbers, and also showed that the Riemann hypothesis is equivalent to a particularly strong upper bound for the error term in the prime number theorem.
At first glance, the Riemann hypothesis might appear to be completely special, a one-of-a-kind conjecture. However, it was not long before DEDEKIND [VI.50] generalized the Riemann hypothesis to a whole family of zeta functions, and in doing so opened the door to further generalization. Just as we can think of the complex numbers as being obtained from the real numbers by including a square root of -1, that is, a root of the polynomial x2 + 1, one can obtain a NUMBER FIELD [III.63], the fundamental object of study in ALGEBRAIC NUMBER THEORY [IV.1], from the field ℚ of rational numbers by including roots of more general polynomials. For each number field K we have the ring of integers ( K, which enjoys many of the same properties as the classical integers ℤ. Starting from this observation, Dedekind defined a more general class of zeta functions, one for each such ring, which now bear his name. The classical zeta function ζ(s) was the Dedekind zeta function in the case (
K, which enjoys many of the same properties as the classical integers ℤ. Starting from this observation, Dedekind defined a more general class of zeta functions, one for each such ring, which now bear his name. The classical zeta function ζ(s) was the Dedekind zeta function in the case (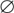 K = ℤ. However, it was not at all straightforward to establish the existence of a functional equation for Dedekind zeta functions: this was an open problem until 1917, when it was settled by Hecke, who showed at the same time that Dedekind zeta functions could be extended to the complex plane, thereby ensuring that the Riemann hypothesis makes sense for them as well.
K = ℤ. However, it was not at all straightforward to establish the existence of a functional equation for Dedekind zeta functions: this was an open problem until 1917, when it was settled by Hecke, who showed at the same time that Dedekind zeta functions could be extended to the complex plane, thereby ensuring that the Riemann hypothesis makes sense for them as well.
With such ideas in the air, it was not long before geometry entered the picture. ARTIN [VI.86] first introduced zeta functions and the Riemann hypothesis for certain curves over finite fields in his 1923 thesis, noting that the ring of polynomial functions on such a curve shares precisely the properties of rings of integers that Dedekind used to define his zeta functions. Artin quickly observed first that his new zeta functions were strongly analogous to Dedekind zeta functions, and second that they were often more tractable: evidence for both observations is provided by the fact that he was able to check explicitly that the Riemann hypothesis was satisfied for a number of specific curves. The difference between the two situations is encapsulated as follows: while in the number field case one can think of the zeta function as counting primes, in the case of a function field the zeta function may be expressed in terms of the more geometric data of counting points on the given curve. In a 1931 paper F. K. Schmidt generalized Artin’s work, and exploited this geometry to prove a strong form of the functional equation for such zeta functions. And then, in 1933, Hasse proved the Riemann hypothesis in the special case of ELLIPTIC CURVES [III.21] over finite fields.
We now discuss in more detail the definition and properties of zeta functions associated with curves over finite fields, as well as the theorems of Schmidt and Hasse. Let  q denote the finite field with q elements, where q = pr for some prime number p and some positive integer r. The simplest case is when q = p, and
q denote the finite field with q elements, where q = pr for some prime number p and some positive integer r. The simplest case is when q = p, and  p is just the field of integers modulo p. More generally, we can obtain
p is just the field of integers modulo p. More generally, we can obtain  q by adding roots of polynomials to
q by adding roots of polynomials to  p just as we do to ℚ to obtain number fields; in fact, a single root of a single irreducible polynomial of degree r will do.
p just as we do to ℚ to obtain number fields; in fact, a single root of a single irreducible polynomial of degree r will do.
Artin studied a certain class of curves in the plane. Here, “plane” means 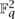 , that is, the set of all pairs (x,y) with x and y in
, that is, the set of all pairs (x,y) with x and y in  q. A curve C is simply the subset of these points where some polynomial f (x,y) with coefficients in
q. A curve C is simply the subset of these points where some polynomial f (x,y) with coefficients in  q vanishes. Of course, if F is any field that contains
q vanishes. Of course, if F is any field that contains  q, then the coefficients are also in F, so it makes sense to talk about C(F), the curve in the larger “plane” F2 defined by the same equation f (x,y) = 0. If F is also a finite field, then C(F) is obviously also finite. The finite fields F containing
q, then the coefficients are also in F, so it makes sense to talk about C(F), the curve in the larger “plane” F2 defined by the same equation f (x,y) = 0. If F is also a finite field, then C(F) is obviously also finite. The finite fields F containing  q turn out to be the fields
q turn out to be the fields  qm for m ≥ 1. For each m ≥ 1 let us define Nm(C) to be the number of points belonging to the curve C(
qm for m ≥ 1. For each m ≥ 1 let us define Nm(C) to be the number of points belonging to the curve C( qm). The sequence N1(C),N2(C),N3(C), . . . is what we shall try to understand.
qm). The sequence N1(C),N2(C),N3(C), . . . is what we shall try to understand.
Given our plane curve C, we can define the ring of polynomial functions 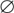 C of C. This is simply the ring of polynomial functions on the plane (i.e., in two variables), modulo the EQUIVALENCE RELATION [I.2 §2.3] that two functions taking the same values on C should be considered the same. Formally,
C of C. This is simply the ring of polynomial functions on the plane (i.e., in two variables), modulo the EQUIVALENCE RELATION [I.2 §2.3] that two functions taking the same values on C should be considered the same. Formally, 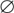 C is simply the QUOTIENT [I.3 §3.3] ring
C is simply the QUOTIENT [I.3 §3.3] ring  q[x,y] / (f(x,y)). Artin’s basic observation was that the definition of the Dedekind zeta function could be applied equally well to the ring
q[x,y] / (f(x,y)). Artin’s basic observation was that the definition of the Dedekind zeta function could be applied equally well to the ring 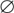 c, yielding a zeta function ZC(t) associated with C. However, in our geometric context we have the following equivalent and more elementary formula, which explicitly relates ZC(t) to the number of points over finite fields:
c, yielding a zeta function ZC(t) associated with C. However, in our geometric context we have the following equivalent and more elementary formula, which explicitly relates ZC(t) to the number of points over finite fields:
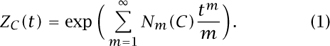
Schmidt generalized Artin’s definition to all curves over finite fields, and gave an elegant description of the zeta function for curves, bearing out Artin’s observations in the cases he was able to compute. The nicest form of Schmidt’s theorem applies to curves that satisfy two additional conditions. The first condition is that, rather than considering the curve C in the plane, we will want to “compactify” it by considering instead a projective curve; we can think of this as adding some “points at infinity,” thus increasing Nm(C) slightly. Second, we will want to impose a technical condition of smoothness on C, which is analogous to asking that C be a MANIFOLD [I.3 §6.9].
In order to state Schmidt’s result, recall that there is a notion of the GENUS [IV.4 §10] of a smooth projective curve C, which can be defined to be the dimension g of the space of differentials on C, or, if C is a complex curve, as the “number of holes” in the space obtained from the analytic topology on C. By extending certain classical results in algebraic geometry to more general fields, Schmidt proved that, for a smooth projective curve C over  q of genus g, we have
q of genus g, we have
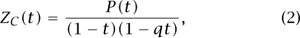
where P(t) is a polynomial of degree 2g with integer coefficients. Furthermore, he proved a functional equation in terms of the substitution t ↦ 1/qt. If we set t = q-s, this gives a functional equation for the substitution s ↦ 1 - s, as in Riemann’s original work. The Riemann hypothesis for C is then the statement that the roots of ZC (q-s) all have Re(s) =  , or, equivalently, that the roots of P(t) all have norm equal to q-1/2. It is an elementary observation that this is equivalent to the assertion that |Nm(C) - qm + 1| ≤ 2g
, or, equivalently, that the roots of P(t) all have norm equal to q-1/2. It is an elementary observation that this is equivalent to the assertion that |Nm(C) - qm + 1| ≤ 2g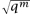 for all m ≥ 1.
for all m ≥ 1.
The next step in exploiting the geometric nature of zeta functions of curves is the observation that if F is a finite field containing  qm, then the points with coordinates in
qm, then the points with coordinates in  qm are the fixed points of a function called the Frobenius map, which is the map
qm are the fixed points of a function called the Frobenius map, which is the map  qm that sends a point (x,y)
qm that sends a point (x,y)  F2 to the point
F2 to the point 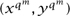 . It is a simple extension of FERMAT’S LITTLE THEOREM [III.58] that if t
. It is a simple extension of FERMAT’S LITTLE THEOREM [III.58] that if t 
 qm, then
qm, then 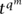 = t. Moreover, the converse holds: if F is a field containing
= t. Moreover, the converse holds: if F is a field containing  qm, and t
qm, and t  F satisfies
F satisfies 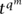 = t, then t
= t, then t 
 qm. This follows because in any field, and in particular in F, the polynomial
qm. This follows because in any field, and in particular in F, the polynomial 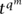 - t can have at most qm roots, which must then be precisely the elements of
- t can have at most qm roots, which must then be precisely the elements of  qm. It immediately follows that a point (x,y)
qm. It immediately follows that a point (x,y)  F2 is a fixed point of
F2 is a fixed point of  qm if and only if (x,y)
qm if and only if (x,y) 
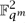 . Moreover, it is elementary that
. Moreover, it is elementary that 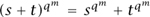 if s, t are in any field containing
if s, t are in any field containing  qn. Because the coefficients of f(x,y) are in
qn. Because the coefficients of f(x,y) are in  qm, it follows that if f(x,y) = 0, then
qm, it follows that if f(x,y) = 0, then
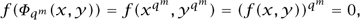
so we see that  qm gives a map from C to itself. Thus, one might hope to study C (
qm gives a map from C to itself. Thus, one might hope to study C ( qm by analyzing more generally what one can say about the fixed points of maps from C to itself. Hasse successfully applied this point of view to prove the Riemann hypothesis in the case g = 1, which is to say the case of elliptic curves. Moreover, we will see that this perspective is woven throughout the fabric of the rest of our story, not only inspiring Weil to make his conjectures, but also suggesting the techniques that ultimately led to their proof.
qm by analyzing more generally what one can say about the fixed points of maps from C to itself. Hasse successfully applied this point of view to prove the Riemann hypothesis in the case g = 1, which is to say the case of elliptic curves. Moreover, we will see that this perspective is woven throughout the fabric of the rest of our story, not only inspiring Weil to make his conjectures, but also suggesting the techniques that ultimately led to their proof.
In 1940 and 1941, Weil gave two proofs of the Riemann hypothesis for curves over finite fields. Or, to be more accurate, he described two proofs: they both relied on fundamental facts in algebraic geometry which had been proved by analytic methods for varieties over the complex numbers, but which had not been proved rigorously in the case of arbitrary base fields. It was largely in order to address this deficiency that Weil wrote his Foundations of Algebraic Geometry, which appeared in 1948 and allowed both of his earlier proofs to be made rigorous.
Weil’s book constituted a watershed in algebraic geometry, as it introduced for the first time the notion of an abstract algebraic variety. Previously, a variety was always a global object, in that it was defined by a single collection of polynomial equations, in either affine or projective space. Weil realized that it would be helpful to have a corresponding locally defined concept, so he introduced abstract algebraic varieties, which are obtained by gluing together affine algebraic varieties in much the same way that manifolds in topology are obtained by gluing together open subsets of affine space. The notion of an abstract variety played a fundamental role in formalizing Weil’s proofs, and was also an important precursor to Grothendieck’s immensely successful theory of SCHEMES [IV.5 §3].
The following year, in a remarkable paper in the Bulletin of the American Mathematical Society, Weil went further, studying zeta functions ZV(t) associated with higher-dimensional varieties V over finite fields, and taking as his definition the formula (1). While the situation is more complicated in this context, the behavior conjectured by Weil was nonetheless strikingly similar, an utterly natural extension of the case of curves:
(i) ZV(t) is a rational function of t;
(ii) more explicitly, if n = dim V, we can write
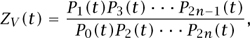
where each root of each Pi(t) is a complex number of normq-i / 2
(iii) the roots of Pi(t) are interchanged with the roots of P2n-i (t) under the substitution t ↦ 1/qnt;
(iv) if V is the reduction modulo p of a variety 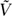 defined over a subfield of ℂ, then bi = deg Pi(t) is the ith Betti number of
defined over a subfield of ℂ, then bi = deg Pi(t) is the ith Betti number of 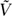 using the usual topology.
using the usual topology.
The last part of (ii) is known as the Riemann hypothesis, while (iii) constitutes a functional equation for the substitution t ↦ 1/qnt. Betti numbers are a well-known invariant from ALGEBRAIC TOPOLOGY [IV.6]: if we return to Schmidt’s theorem (2) in the case of curves, the degrees 1, 2g, 1 of 1 - t, P(t), 1 - qt are precisely the Betti numbers of a complex curve of genus g.
Weil’s conjectures were inspired by a very intuitive topological picture, derived from considering V( qm) as the set of fixed points of
qm) as the set of fixed points of  qm. Forgetting for the moment that
qm. Forgetting for the moment that  qm makes sense only over finite fields, if we imagine that V were defined over the complex numbers, then by using the complex topology we could study the fixed points of
qm makes sense only over finite fields, if we imagine that V were defined over the complex numbers, then by using the complex topology we could study the fixed points of  qm by the LEFSCHETZ FIXED POINT THEOREM [V.11 §3], obtaining a formula in terms of the action of
qm by the LEFSCHETZ FIXED POINT THEOREM [V.11 §3], obtaining a formula in terms of the action of  qm on the COHOMOLOGY GROUPS [IV.6 §4]. Indeed, we could deduce the factorization in (ii) almost immediately (and in particular the rationality asserted in (i)), with each factor Pi(t) corresponding to the action of Frobenius on the ith cohomology group, and we would also have deg Pi(t) given by the ith Betti number of V. Moreover, the functional equation would follow from a concept known as POINCARÉ DUALITY [III.19 §7].
qm on the COHOMOLOGY GROUPS [IV.6 §4]. Indeed, we could deduce the factorization in (ii) almost immediately (and in particular the rationality asserted in (i)), with each factor Pi(t) corresponding to the action of Frobenius on the ith cohomology group, and we would also have deg Pi(t) given by the ith Betti number of V. Moreover, the functional equation would follow from a concept known as POINCARÉ DUALITY [III.19 §7].
It was not long before it became clear that such cohomological arguments might become more than just motivation: there could be a cohomology theory for algebraic varieties over finite fields that would mimic the properties of the classical topological theory and would allow one to prove the Weil conjectures. Such a cohomology theory is now known as a Weil cohomology. Serre was the first to seriously attempt to develop such a theory, but he had only limited success. In 1960, Dwork provided a brief detour by using p-ADIC ANALYSIS [III.51] to prove parts (i) and (iii) of the conjectures: that is, the rationality and the functional equation. Shortly thereafter, building on comments of Serre and in collaboration with Artin, Grothendieck proposed and developed a candidate for a Weil cohomology, the étale cohomology. Indeed, he noted that one could in fact extend the list of desired properties of a Weil cohomology in such a way that the Weil conjectures would follow almost immediately. These properties were known but extremely difficult in the classical case, and included the “hard Lefschetz theorem.” In a burst of optimism, Grothendieck referred to them as the “standard conjectures,” and envisioned that the Weil conjectures would ultimately be proved through them.
However, the final chapter of the story did not go entirely according to Grothendieck’s plan. His student Deligne set about working on the problem, and was ultimately able to complete an exceedingly subtle and intricate proof using induction on the dimension of the variety. The étale cohomology played an absolutely fundamental role in Deligne’s proof, but he also introduced other ideas into the picture, most notably a classical geometric construction of Lefschetz, as well as some work of Rankin on the Ramanujan conjecture. In the end, he was able to conclude the hard Lefschetz theorem from his work, but the rest of the standard conjectures remain unsolved to this day.
Acknowledgments. I would like to thank Kiran Kedlaya, Nicholas Katz, and Jean-Pierre Serre for their helpful correspondence.
Dieudonné, J. 1975. The Weil conjectures. Mathematical Intelligencer 10:7–21.
Katz, N. 1976. An overview of Deligne’s proof of the Riemann hypothesis for varieties over finite fields. In Mathematical Developments Arising from Hilbert Problems, edited by F. E. Browder, pp. 275–305. Providence, RI: American Mathematical Society.
Weil, A. 1949. Numbers of solutions of equations in finite fields. Bulletin of the American Mathematical Society 55: 497–508.