
b. Clermont-Ferrand, France, 1623; d. Paris, 1662
Scientist and theologian
Pascal was the first to make a systematic study of the arithmetical triangle which now bears his name; although the triangle itself is found earlier, notably in the work of the Chinese mathematician Zhu Shijie (1303). “Pascal’s triangle”

a triangular array in which each number is the sum of the two immediately above it, provides a geometrical arrangement of the binomial coefficients 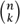 , with
, with 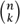 appearing as the (k + 1)st element in the (n + 1)st row. Here
appearing as the (k + 1)st element in the (n + 1)st row. Here 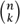 is, as usual, the number of subsets of size k in a set of size n, so that
is, as usual, the number of subsets of size k in a set of size n, so that
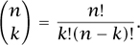
The number 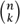 is also the coefficient of ak bn − k in the binomial expansion of (a + b)n for any integer n ≥ 0 and 0 ≤ k ≤ n. In his Traité du Triangle Arithmétique (printed in 1654 but not distributed until 1665) Pascal was the first to connect binomial coefficients with the combinatorial coefficients that arise in probability. The Traité is famous too for its explicit statement of the principle of mathematical induction.
is also the coefficient of ak bn − k in the binomial expansion of (a + b)n for any integer n ≥ 0 and 0 ≤ k ≤ n. In his Traité du Triangle Arithmétique (printed in 1654 but not distributed until 1665) Pascal was the first to connect binomial coefficients with the combinatorial coefficients that arise in probability. The Traité is famous too for its explicit statement of the principle of mathematical induction.
Pascal is also known for a theorem in projective geometry (given an arbitrary hexagon inscribed in any conic section, if the three pairs of opposite sides are continued until they meet, then the three points of intersection lie on a straight line) (1640); and for a two-function (addition and subtraction) mechanical calculating machine (1645).