b. Edmonton, Middlesex, England, 1685; d. London, 1731
Secretary of the Royal Society (1714–18)
Taylor was not the first to discover the theorem that bears his name (James Gregory found the theorem in 1671), but he was the first to publish it and the first to appreciate its significance and applicability. The theorem, which states that any function that satisfies certain conditions can be expressed as (what is now known as) a Taylor series, was published in Taylor’s Methodus Incrementorum Directa et Inversa (1715). In the Methodus Taylor gave the series as
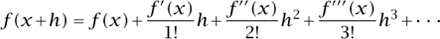
(as it would appear in modern notation). Although Taylor did not attend to questions of rigor—there is no consideration of convergence, of the remainder term, or of the validity of expressing a function by such a series—his derivation of the series was not out of line with the standards of its day. Taylor used the theorem for approximating the roots of equations and for solving differential equations. Although he was aware of its use for expanding functions into series, he does not appear to have fully appreciated its significance in this respect.
Taylor is also noted for his contribution to the problem of the vibrating string (discussed in the Methodus and in earlier papers) and for a book on the theory of linear perspective (1715).