The Princeton Companion to Mathematics

VI.18 The Bernoullis

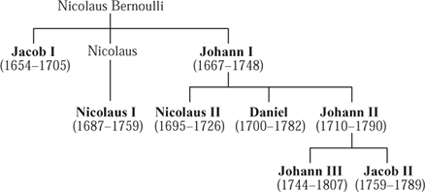
All born in Basel, Switzerland, apart from Daniel (Groningen, the Netherlands). All died in Basel, apart from Jacob II, Nicolaus II (both Saint Petersburg, Russia), and Johann III (Berlin). (The two members of the family not in bold text were not mathematicians.)

The Bernoullis played a remarkable role in the development of mathematics during the Enlightenment. Indeed such was the family’s importance that in 1715 LEIBNIZ [VI.15] coined the term “bernoullizare” to describe the activity of doing mathematics. Altogether eight members of the family devoted themselves to the mathematical sciences (including physics, especially mechanics and fluid mechanics), and from 1687 to 1790 the mathematics chair of the university of Basel was occupied by successive members of the family: first Jacob (1687–1705), then his brother Johann (1705–48), and finally Johann’s son, Johann 11 (1748–90). Throughout the eighteenth century Bernoullis were members of the Paris Academy of Sciences and individually they won prestigious prizes on many occasions. The same was true of the academies in Berlin, Saint Petersburg, and several others.

The family goes back to a line of Calvinist merchants who fled the Spanish Netherlands. The first Bernoulli to settle in Basel was Jacob, a druggist, who became a citizen in 1622. His grandson, Jacob I, studied philosophy and theology in Basel before turning to mathematics, against the will of his father. This was to be a typical pattern in the family: many of the Bernoullis studied mathematics despite pressure from the family to make a career in other areas (such as medicine or law). Having received a licentiate in theology in 1676, Jacob undertook an educational journey which took him first to France, then to the Netherlands, and finally to England. And it was through his encounters with Nicolas Malebranche, Jan Hudde, and others that he became acquainted with Cartesianism and its most eminent representatives. In 1677 he started his diary, Meditationes, in which he wrote down many of his mathematical insights and thoughts.

Having obtained the chair of mathematics in Basel, Jacob studied Leibniz’s early memoirs on differential calculus, whose power he was the first, together with his younger brother Johann I, to recognize. In a paper on the curve of constant descent, published in the Leipzig Acta Eruditorum in 1690, Jacob was the first to use the term “integral” in its present mathematical sense. From then on he showed his mastery of Leibnizian methods in his study of curves, including, among others, the catenary, the form of a bent elastic beam, the form of a sail inflated by the wind, and the parabolic and logarithmic spirals. He also solved the differential equation y′ = p(x)y + q(x)yⁿ, which is now named after him. However he is best remembered for his Ars Conjectandi (1713), which was published posthumously with a short foreword by his nephew, Nicolaus I. It contains an attempt to give a sound mathematical treatment of a commonsense principle already appealed to by CARDANO [VI.7] and Halley: if an experiment is repeated a large number of times, then the relative frequency with which an event occurs will roughly equal the probability of the event. Bernoulli’s theorem, known since POISSON [VI.27] as the (WEAK) LAW OF LARGE NUMBERS [III.71 §4], establishes a first link between the theories of probability and statistics. In the same book, Bernoulli also introduced the sequence B₀, B₁, . . . of rational numbers that now bears his name, which can be defined as the coefficients of t^k/k! in the power-series expansion

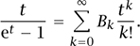
Jacob computed these numbers up to B₁₀.

Johann, who had to study medicine before he could devote himself to mathematics, got his first mathematical training from his brother Jacob, with whom he developed numerous applications of the new Leibnizian calculus to mechanics. An academic peregrination brought him to Paris in 1691–92, where he gave private lessons to Guillaume de l’Hôpital. These lessons are the basis of l’Hôpital’s famous Analyse des Infiniment Petits (1696). This textbook, the first on calculus, contains l’Hôpital’s rule, which Johann had communicated by letter to his student. In 1695, Johann left Basel for Groningen to take up a professorship in mathematics.

With the growing visibility of Johann’s work, the friendly collaboration between the two brothers Jacob and Johann transformed into an endless round of controversies, priority disputes, and public accusations. They engaged in heated struggles concerning the solution of the brachistochrone (curve of fastest descent) problem, and a complicated isoperimetric problem that involved minimizing the area enclosed by a curve of fixed length. Eventually, these bitter quarrels led to an interesting mathematical outcome: the creation of the CALCULUS OF VARIATIONS [III.94]. After Jacob’s death, Johann took over the mathematics chair in Basel, where he taught until the end of his life, attracting students from all over Europe, including EULER [VI.19].

Johann’s most important achievement in mathematics is the development of the integral calculus. He developed a general theory for the integration of rational functions and new methods for the solution of differential equations. He also extended the infinitesimal calculus to handle EXPONENTIAL FUNCTIONS [III.25].

Johann’s correspondence with Leibniz (which spans approximately twenty-five years) can be viewed as a laboratory of mathematical invention and debate. The priority dispute that ensued when NEWTON [VI.14] accused Leibniz of having stolen the calculus from him also involved Johann, who fought on Leibniz’s side. With each camp defying the other with difficult problems, Johann had the opportunity to create, with his son Nicolaus II, the theory of orthogonal trajectories of families of curves. Johann was also a towering figure in the origins of analytical mechanics and in mathematical physics, where, among other things, he made notable contributions to the study of central forces, to navigational theories, and to the question of the principles of statics.

Nicolaus I studied mathematics at the university of Basel with his uncle Jacob before taking a degree of Doctor of Jurisprudence (1709). He was the professor of mathematics in Padua, occupying the chair once held by Galileo, and he later held the professorship of logic in Basel. His main interests in mathematics were infinite series and the applications of probability theory to questions of law. He formulated, in 1713, the notorious Saint Petersburg paradox, which originated with a gambling game. Suppose that Peter is tossing a fair coin, and he will give Paul one ducat if the coin turns up heads on the first toss, two ducats if it shows heads for the first time on the second toss, and in general 2^{n − 1} ducats if the coin turns up heads for the first time on the nth toss. 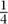The standard calculation shows that the value of Paul’s expectation (E = 1 + 2 + 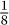4 + . . . + 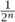2ⁿ⁻¹ · · ·) is infinitely great. Nevertheless no “fairly reasonable man” would be willing to pay even a moderately high price to purchase Paul’s prospects. The result of the mathematical analysis clearly affronted common sense; this was the paradox. Nicolaus’s cousin, Daniel, discussed the problem while he was staying in Saint Petersburg (hence the name given to the paradox). His strategy was to distinguish two senses of expectation, one mathematical and the other moral. The latter was to take into account the individual characteristics of the risk taker (his wealth, for instance).

Although primarily a physicist and author of the famous Hydrodynamica (1738), Daniel obtained a solution of the Riccati equation, y′ = r(x) + p(x)y + q(x)y², and engaged in the problem of the vibrating string.

Otto Spiess, from Basel, started to publish the complete edition of the works and correspondence of the Bernoullis in 1955. The project continues.

VI.18 The Bernoullis

Further Reading