b. Nottingham, England, 1793; d. Nottingham, 1841
Miller, Fellow of Caius College, Cambridge (1839-41)
Green, a self-taught mathematician, went to Cambridge University at the age of forty, having already produced his most important work, the privately printed An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism (1828). In this work, which Green opened by stressing the central role of the “potential function” (a term that he himself coined), he proved the three-dimensional version of the theorem now named after him, and introduced the concept that RIEMANN [VI.49] later called Green’s function (1860). The Essay became widely known only after its discovery in 1845 by William Thomson (later Lord Kelvin), who was responsible for its republication in the Journal für die reine und angewandte Mathematik (1850-54).
Green gave his version of the theorem (in modern notation) as
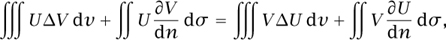
where U and V are two continuous functions of x, y,, z whose derivatives are not infinite at any point of an arbitrary body, n is the surface normal of the body directed inward, and dσ is a surface element. The result today known as Green’s theorem, which is the planar version of the above, was first published by CAUCHY [VI.29] in 1846, and it can be given (in modern notation) as follows. Let R be a closed plane region with a piecewise-smooth boundary curve C with positive orientation. Let P(x, y) and Q (x,y), having continuous partial derivatives, be defined on an open region containing R. We then have
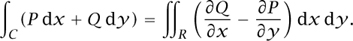
More original than his theorem, however, was the powerful technique Green developed to solve certain second-order differential equations. In essence, Green sought a “potential function” and formulated the conditions it needed to satisfy. His great insight was to recognize that the central issue in potential theory was to relate properties inside volumes to properties on their surfaces. Green’s functions are extensively used today in the solution of inhomogeneous differential equations with boundary conditions and in the solution of partial differential equations.