b. Düren, French Empire (now Germany), 1805;
d. Göttingen, Germany, 1859
Number theory; analysis; mathematical physics; hydrodynamics;
probability theory
The low level of mathematics education at German universities prompted Dirichlet to study in Paris, where he came into contact with the leading French mathematicians Lacroix, POISSON [VI.2 7], and FOURIER [VI.2 5], who particularly attracted him. In 1827 he took up a position at the University of Breslau. The following year he moved to Berlin, where he was appointed as a professor at the military academy and where he was also allowed to teach at the university. In 1831 he was made a professor at the university and from then on held positions at both institutions until 1855, when he was appointed as the successor to GAUSS [VI.26] at the University of Göttingen.
Dirichlet’s primary interest was in number theory. His guiding star was Gauss’s pioneering Disquisitiones Arithmeticae (1801)—the work that made number theory into a mathematical discipline—which he studied throughout his career. Dirichlet was not only the first mathematician to completely understand this work but he also became its interpreter, picking up its problems and improving its proofs, as well as developing its ideas.
With his very first publication, which appeared in 1825, Dirichlet came to international prominence. The paper, which dealt with Diophantine equations of the form x5 + y5 = Az5, yielded substantial results for the verification of FERMAT’S LAST THEOREM [V.10] for the case n = 5 (these results were used by LEGENDRE [VI.24] for a complete proof for that case some weeks later). In a paper published in 1837 Dirichlet came up with the new and revolutionary idea of applying analytical methods to number theory. He introduced expressions that are now known as Dirichlet L-series. These are infinite series of the form
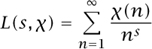
where χ(n) is a Dirichlet character modulo k: that is, a complex-valued function on the integers that is totally multiplicative, in the sense that χ(ab) = χ(a) χ (b) for all a and b, and χ is periodic with period k and not identically zero. Using these L-series, Dirichlet showed that every arithmetic progression {an + b : n = 0, 1, . . . }, where a and b are relatively prime, contains infinitely many prime numbers. In two subsequent papers, published in 1838 and 1839, he used his new methods, among other things, to determine the formula of the class number of binary quadratic forms: that is, the number of proper classes of forms of given determinant. It is often said that these three papers mark the start of ANALYTIC NUMBER THEORY [IV.2].
Dirichlet also made important contributions to algebraic number theory, culminating in his UNIT THEOREM [III.63] for the Abelian group of units in an algebraic number field. These contributions, together with numerous others due to him (e.g., his Schubfachprinzip, or box principle; work on the law of biquadratic reciprocity; and results concerning Gaussian sums), were brought together in his influential Vorlesungen über Zahlentheorie (lectures on number theory), published by his former student DEDEKIND [VI.50] in 1863.
Inspired by his close contact with FOURIER [VI.25] during his student days in Paris, Dirichlet’s other main interests were in analysis and mathematical physics, and in the connections between them. In a groundbreaking paper of 1829, Dirichlet not only gave the first strict proof of the convergence of a Fourier series under given conditions, but he also used new methods and concepts (e.g., his insight into the importance of conditional convergence of series; his Dirichlet function influencing the development of the concept of a function) that became classic and that served as a basis for countless nineteenth-century investigations on analysis. He also occupied himself with the determination of multiple integrals as well as with the expansion of a function into spherical functions (Kugelfunktionen) and applied these results to problems in mathematical physics. His main contributions to mathematical physics include papers on the theory of heat, hydrodynamics, the gravitational attraction of an ellipsoid, the n-body problem, and potential theory. The first boundary-value problem (the “Dirichlet problem” of finding the solution of an elliptic partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region) had already been handled by Fourier and others, but Dirichlet proved the uniqueness of the solution, while the DIRICHLET PRINCIPLE [IV.12 §3.5] (a method for solving boundary problems for ELLIPTIC PARTIAL DIFFERENTIAL EQUATIONS [IV.12 §2.5] by reducing them to VARIATIONAL PROBLEMS [III.94]) was introduced by him in lectures on potential theory, enhancing a method introduced by Gauss. Connected with Dirichlet’s work on analysis was his contribution to probability and error theory, in particular his development of new methods for probabilistic limit theorems.
Dirichlet also influenced the further development of mathematics by his mathematical style, by the exactness and elegance of his proofs, and by his teaching. Together with his friend JACOBI [VI.35], he ushered in a new epoch of mathematical teaching at German universities by introducing lectures and seminars on the most recent research, and with him began the golden age of mathematics in Berlin. Although Dirichlet did not found his own mathematical school, his influence can be found in the work of Dedekind, Eisenstein, KRONECKER [VI.48], and RIEMANN [VI.49], among others.
Butzer, P.-L., M. Jansen, and H. Zilles. 1984. Zum bevorstehenden 125. Todestag des Mathematikers Johann Peter Gustav Lejeune Dirichlet (1805-1859), Mitbegründer der mathematischen Physik im deutschsprachigen Raum. Sudhoffs Archiv 68:1-20.
Kronecker, L., and L. Fuchs, eds. 1889-97. G. Lejeune Dirichlet’s Werke, two volumes. Berlin: Reimer.