VI.39 Joseph Liouville
b. Saint Omer, France, 1809; d. Paris, 1882
Differentiation of arbitrary order; integration in closed form;
Sturm-Liouville theory; potential theory; mechanics;
differential geometry; doubly periodic functions;
transcendental numbers; quadratic forms
Liouville was the leading French mathematician in the generation between CAUCHY [VI.29] and HERMITE [VI.47]. He taught analysis and mechanics at his alma mater, the École Polytechnique, until 1851, when he became professor at the Collège de France. Moreover, he was professor at the Sorbonne from 1857 and member of the Paris Academy of Sciences and the Bureau des Longitudes. In 1836 he founded the Journal de Mathématiques Pures et Appliquées, which exists to this day.
His wide-ranging research was often inspired by physics. For example, his early theory of differential operators of the form (d/dx)k, where k is an arbitrary complex number, had its origin in Ampère’s electrodynamics. Similarly, Sturm-Liouville theory, which he developed in around 1836 with his friend C. F. Sturm, was inspired by the theory of heat conduction. Sturm-Liouville theory deals with a linear self-adjoint second-order differential equation involving a parameter that must be chosen so that there exist nontrivial solutions (eigenfunctions) that satisfy given boundary-value conditions. Liouville’s main contribution to this theory was a proof that an “arbitrary” function has a convergent “Fourier expansion” in terms of eigenfunctions. Sturm-Liouville theory was a major step toward a more qualitative theory of differential equations, and the first work on spectral theory of a general class of differential operators.
In 1844 Liouville gave the first proof that there exist TRANSCENDENTAL NUMBERS [III.41], of which a well-known example is 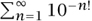 . In a similar vein, in the 1830s he had already shown that there are elementary functions such as e t / t whose integrals are not expressible in elementary (or closed) form, i.e., in terms of algebraic functions, exponentials, and logarithms. In particular he proved that the elliptic integrals are nonelementary.
. In a similar vein, in the 1830s he had already shown that there are elementary functions such as e t / t whose integrals are not expressible in elementary (or closed) form, i.e., in terms of algebraic functions, exponentials, and logarithms. In particular he proved that the elliptic integrals are nonelementary.
Around 1844 Liouville suggested an entirely new approach to ELLIPTIC FUNCTIONS [V.31] (inverses of elliptic integrals), based on a systematic investigation of doubly periodic complex functions and in particular the observation that such a function must have singularities if it is not constant. When Cauchy heard of this theorem he immediately generalized it to the statement that any bounded complex analytic function must be a constant. Today this is called Liouville’s theorem.
In mechanics, Liouville’s name is connected with the theorem stating that the volume in phase space is constant when a mechanical system moves according to HAMILTON’S EQUATIONS [III.88 §2.1]. In fact, Liouville proved the constancy of a certain DETERMINANT [III.15] formed from the solutions of a general class of differential equations. It was JACOBI [VI.35] who pointed out that the theorem applied to Hamilton’s equations, and Boltzmann who interpreted the determinant as the volume in phase space, and emphasized its importance in statistical mechanics.
Liouville made many other important contributions to mechanics and to potential theory. For example, Jacobi had postulated that when the angular momentum of a fluid planet revolving around an axis is high enough, there are two shapes that are in equilibrium in their rotating frames of reference: an ellipsoid of revolution and an ellipsoid with three different axes. Liouville showed that Jacobi was right, and moreover proved the surprising result that only the latter figure is in stable equilibrium. Liouville published only the result, leaving the verification to Lyapunov and POINCARÉ [VI.61] (at least if the angular momentum is not too large).
The first mathematician to recognize the significance of GALOIS’S [VI.41] theory of SOLVABILITY OF EQUATIONS [V.20], Liouville did a great service to algebra when he published some of Galois’s most important papers in his journal.
Further Reading
Lützen, J. 1990. Joseph Liouville 1809-1882: Master of Pure and Applied Mathematics. Studies in the History of Mathematics and Physical Sciences, volume 15. New York: Springer.
Jesper Lützen
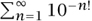 . In a similar vein, in the 1830s he had already shown that there are elementary functions such as e t / t whose integrals are not expressible in elementary (or closed) form, i.e., in terms of algebraic functions, exponentials, and logarithms. In particular he proved that the elliptic integrals are nonelementary.
. In a similar vein, in the 1830s he had already shown that there are elementary functions such as e t / t whose integrals are not expressible in elementary (or closed) form, i.e., in terms of algebraic functions, exponentials, and logarithms. In particular he proved that the elliptic integrals are nonelementary.