b. Sorau (now Zary, Poland), 1810; d. Berlin, 1893
Gymnasium teacher, Liegnitz (now Legnica, Poland) 1832-42;
Professor of Mathematics: Breslau (now Wroclaw, Poland) 1842-55,
Berlin 1855-82
Kummer’s early research was in function theory, in which he made an important contribution to the theory of the (generalized) hypergeometric series (a power series in which the ratios of successive coefficients are rational functions). Surpassing earlier work of GAUSS [VI.26], Kummer not only provided a systematic account of solutions to the hypergeometric differential equation
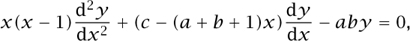
where a, b, and c are constants, but also made the connection between the hypergeometric functions and newer functions in analysis, such as the ELLIPTIC FUNCTIONS [V.31].
After moving to Breslau, Kummer started doing research in number theory, the field in which he achieved his greatest success: the creation of the theory of “ideal prime factors” (1845-47). Although Kummer’s theory is often described as an early contribution to the theory of IDEALS [III.81 §2], his algorithmic approach was very different from that later followed by DEDEKIND [VI.50]. Kummer’s original goal had been to generalize the LAW OF QUADRATIC RECIPROCITY [V.28] to higher powers, and he succeeded in this in 1859. An additional consequence of this research was that he managed to prove FERMAT’S LAST THEOREM [V.10] for all prime exponents (and hence, since it was known for fourth powers, all exponents) less than 100.
In the third phase of his career Kummer turned to algebraic geometry. Continuing the work of HAMILTON [VI.37] and JACOBI [VI.35] on ray systems and geometric optics, he was led to the discovery of the quartic surface with sixteen nodal points, which is now named after him.