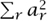 is convergent; further, f is itself square summable. He proved the theorem in 1907, simultaneously with the German mathematician Ernst Fischer; so it is named after both of them.
is convergent; further, f is itself square summable. He proved the theorem in 1907, simultaneously with the German mathematician Ernst Fischer; so it is named after both of them.b. Györ, Hungary, 1880; d. Budapest, 1956
Functional analysis; set theory; measure theory
After being educated at Budapest University and elsewhere in Europe, Riesz was appointed in 1911 to the University of Kolozsvár (Hungary), which moved in 1920 to become Szeged University; he served twice as Rector. He returned to Budapest in 1946. Most of Riesz’s research work lay in mathematical analysis enriched with techniques from set and measure theory, and functional analysis.
One of Riesz’s famous results was the converse of a generalization of Parseval’s theorem for FOURIER SERIES [III.27]: given a sequence of orthonormal functions on a finite interval, and a sequence a1, a2, . . . of real numbers, there exists a function f that can be expanded as a Fourier-type series with respect to those functions with the ar as coefficients if and only if 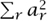 is convergent; further, f is itself square summable. He proved the theorem in 1907, simultaneously with the German mathematician Ernst Fischer; so it is named after both of them.
is convergent; further, f is itself square summable. He proved the theorem in 1907, simultaneously with the German mathematician Ernst Fischer; so it is named after both of them.
Two years later Riesz found the “representation theorem” named after him. It states that a continuous linear functional that maps continuous functions F over a finite interval I onto the real numbers can be represented as a Stieltjes integral of F over I with respect to a function of bounded variation. It was to be a fertile source of applications and generalizations.
VI.75. Luitzen Egbertus Jan Brouwer799
Riesz found these two theorems partly in connection with his study of integral equations, a topic then being developed by HILBERT [VI.63], and partly in connection with his study of functional analysis as formulated by Maurice Fréchet. Hilbert’s work had led him to consider infinite matrices, which were then little studied: Riesz wrote the first monograph on them, Les Systèmes d’Équations Linéaires à une Infinité d′Inconnues (1913). He also studied the theory of Lp spaces for p > 1 (that is, spaces of functions f such that f p is measureintegrable over some specified interval) and their dual spaces Lq, where 1/p + 1/q = 1; and he worked on applying his and Fischer’s theorem to the self-dual space, now known as HILBERT SPACE [III.37], that is given by p = 2. Later he laid some of the foundations of complete spaces (later known as BANACH SPACES [III.62]), and applied functional analysis to ergodic theory. He summed up much of his work in these areas in the book Leçons d’Analyse Fonctionnelle (1952), written with his student B. Szökefnalvy-Nagy.
All this work constituted important contributions to theories already laid out in principle by various other mathematicians. Riesz achieved groundbreaking work on subharmonic functions: he modified the DIRICHLET PROBLEM [IV.12 §1] by allowing the function that extends a given function into a domain to be subharmonic (“locally less than harmonic”) instead of harmonic. He studied some of the applications of these functions to potential theory.
Riesz also studied some foundational aspects of set theory, especially types of ordering, continuity, and generalized Heine-Borel covering theorems. He also reformulated the LEBESGUE INTEGRAL [III.55] in a constructive manner, using step functions and sets of measure zero as primitive notions, and avoiding MEASURE THEORY [III.55] as much as possible.
Riesz, F. 1960. Oeuvres Complètes, edited by Á. Császár, two volumes. Budapest: Akademiai Kiado.