 . If true, this famous conjecture would imply deep results about the distribution of primes. Most of Littlewood’s work on the zeta function was done in collaboration with Hardy and concerned analytic properties of ζ (s).
. If true, this famous conjecture would imply deep results about the distribution of primes. Most of Littlewood’s work on the zeta function was done in collaboration with Hardy and concerned analytic properties of ζ (s).b. Rochester, England, 1885; d. Cambridge, England, 1977 Analysis; number theory; differential equations
Littlewood made important contributions to several different branches of analysis and analytic number theory, including Abelian and Tauberian theory, the RIEMANN ZETA FUNCTION [IV.2 §3], WARING’S PROBLEM, GOLDBACH’S CONJECTURE [V.27], harmonic analysis, probabilistic analysis, and nonlinear differential equations. He loved concrete problems such as the RIEMANN HYPOTHESIS [IV.2 §3]: he was arguably the best problem solver of his generation. Much of his work was done in collaboration with HARDY [VI.73]: the Hardy–Littlewood partnership dominated the mathematical scene in the United Kingdom for a third of a century. With the exception of three years in Manchester, he lived all his adult life in Trinity College, Cambridge. From 1928 until his retirement in 1950, he was the first holder of the Rouse Ball Chair of Mathematics in Cambridge.
His first major result, published in 1911, was a deep converse of ABEL’s [VI.33] classical theorem that if a series of reals Σ an sums to A, then Σ anxn also tends to A as x → 1 from below. In general, the converse is false, but Tauber had proved that it is true if nan → 0. Littlewood extended this by weakening the condition to nan being bounded. This result gave rise to an extended area of analysis called Tauberian theorems.
In the theory of functions, he did elegant, important, and innovative work on injective holomorphic functions, the minimum modulus, and subharmonic functions. In particular, he worked on the conjecture that Bieberbach made in 1916 that if f(z) = z + a2z2 + a3z3 + … is an injective HOLOMORPHIC FUNCTION [I.3 §5.6] in the open disk Δ = {z : | z | < 1}, then | an | ≤ n for every n. Littlewood proved in 1923 that | an | < en for every n. After many improvements by a number of people, the constant e was eventually reduced to a value close to 1, before de Branges proved the full conjecture in 1984.
Littlewood had a lifelong interest in the zeta function. This is defined in the half-plane Re(s) > 1 by the absolutely convergent series and in the whole complex plane by analytic continuation. In fact, the second problem suggested to him by his supervisor was the Riemann hypothesis that the zeros of ζ (s) in the “critical strip” 0 < σ < 1 are on the “critical line” σ =  . If true, this famous conjecture would imply deep results about the distribution of primes. Most of Littlewood’s work on the zeta function was done in collaboration with Hardy and concerned analytic properties of ζ (s).
. If true, this famous conjecture would imply deep results about the distribution of primes. Most of Littlewood’s work on the zeta function was done in collaboration with Hardy and concerned analytic properties of ζ (s).
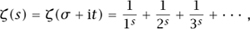
In addition to his work with Hardy, he also made use of the zeta function to prove a striking theorem about the error term in the PRIME NUMBER THEOREM [V.26]. The prime number theorem itself had been proved by HADAMARD [VI.65] and, independently, by DE LA VALLÉE POUSSIN [VI.67] in 1896. This fundamental result states that π(x), the number of primes less than x, is asymptotic to the “logarithmic integral” li(x) =  0x (1 / log t) dt. There was much numerical evidence that π(x) < li(x) for all x; in particular, by 1914 this inequality was known to hold for all 2 ≤ x 107. Nevertheless, Littlewood proved that li(x) – π (x) changes sign infinitely often. Interestingly, he did not obtain any explicit bound for a value x with π(x) > li(x); the first such bound, given by Skewes in 1955, was
0x (1 / log t) dt. There was much numerical evidence that π(x) < li(x) for all x; in particular, by 1914 this inequality was known to hold for all 2 ≤ x 107. Nevertheless, Littlewood proved that li(x) – π (x) changes sign infinitely often. Interestingly, he did not obtain any explicit bound for a value x with π(x) > li(x); the first such bound, given by Skewes in 1955, was
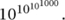
Hardy and Littlewood proved important approximate formulas for ζ (s), which they used to deduce that, in a certain sense, ζ (s) is “small” on the critical line; this was viewed as a breakthrough. Littlewood also studied the number of zeros of ζ (s) in a rectangle 0 < σ < 1, 0<t ≤ T.
In 1770, in his Meditationes Algebraicae, WARING [VI.21] asserted on the basis of empirical evidence that every natural number is the sum of nine nonnegative integral cubes, nineteen fourth powers, and so on: for every natural number k there is a minimal integer g(k) such that every natural number is the sum of g(k) nonnegative kth powers. In 1909 HILBERT [VI.63] used complicated algebraic identities to prove that g(k) indeed exists, but the bounds he obtained on g(k) were rather weak. In the 1920s, in a groundbreaking series of papers entitled Partitio Numerorum, Hardy and Little-wood introduced an analytic method that could be used to tackle not only Waring’s problem of determining g(k), but many other problems as well. The origins of this “circle method” of Hardy and Littlewood go back to the work of Hardy and RAMANUJAN [VI.82] on the partition function, but the technical difficulties that Hardy and Littlewood had to overcome were much greater than in that earlier work. This method enabled them to show, for example, that every sufficiently large number is the sum of nineteen fourth powers. (In 1986, Balasubramanian, Dress, and Deshouillers proved that g(4) is indeed 19.) More importantly, they gave an asymptotic estimate for the number of representations of n as a sum of at most s positive kth powers.
The circle method also provides a possible line of attack on Goldbach’s conjecture that every even number greater than two is the sum of two primes, and gives strong heuristic evidence for the strengthened version of the twin prime conjecture that the number of primes p ≤ n such that p + 2 is also a prime is asymptotic to c 2n (1/(log t)2) dt for a constant c >0. The so-called k-tuple conjecture of Hardy and Littlewood is a further extension of this conjecture for “constellations of primes.”
2n (1/(log t)2) dt for a constant c >0. The so-called k-tuple conjecture of Hardy and Littlewood is a further extension of this conjecture for “constellations of primes.”
Much of Littlewood’s remarkable work on harmonic analysis was done in collaboration with R. E. A. C. Paley in the early 1930s. The starting point of the LITTLEWOOD–PALEY THEORY [VII.03 §7] is an inequality concerning trigonometric polynomials. Roughly speaking, Littlewood and Paley related the size of a function to the projection of its FOURIER COEFFICIENTS [III.27] onto various intervals. The original one-dimensional Littlewood–Paley theory has been extended to higher dimensions, arbitrary intervals, and even to tensors on two-dimensional compact manifolds; the theory has connections to such varied topics as WAVELETS [VII.03], semigroups acting on Lp-spaces of functions with values in a BANACH SPACE [III.62], and the geometry of null hypersurfaces for rough Einstein metrics.
Littlewood was also a formidable applied mathematician. During World War I he worked on ballistics, and during World War II, with his collaborator Mary Cartwright, he worked on the van der Pol oscillator in order to help the development of radio. Cartwright and Littlewood were among the first to combine topological and analytical methods to tackle differential equations, and discovered many of the phenomena that later became known as “chaos”: they proved that chaos could arise even in equations originating in real engineering problems.
From 1910 until his death sixty-seven years later, Littlewood lived in the same set of spacious rooms in Trinity College, Cambridge. He was a great raconteur: after almost every dinner he was to be found in the Combination Room drinking claret in the company of Fellows and any mathematicians who might be visiting. In spite of his tremendous output, he suffered for decades from severe bouts of depression, from which he was cured only in 1957. He practiced his belief that mathematicians should take a vacation of at least twenty-one days a year during which they should do no mathematics. He was a keen and skilled rock climber and an avid Alpine skier. Although not an active musician, on most days he listened to Bach, Beethoven, and Mozart for hours on end.
In 1943, when he was awarded the Sylvester Medal of the Royal Society, the citation read: “Littlewood, on Hardy’s own estimate, is the finest mathematician he has ever known. He was the man most likely to storm and smash a really deep and formidable problem; there was no one else who could command such a combination of insight, technique and power.”
Littlewood, J. E. 1986. Littlewood’s Miscellany, edited and with a foreword by B. Bollobás. Cambridge: Cambridge University Press.
Béla Bollobás