VI.87 Alfred Tarski
b. Warsaw, 1901; d. Berkeley, California, 1983
Symbolic logic; metamathematics; set theory; semantics; model
theory; algebras of logic; universal algebra; axiomatic geometry
Tarski matured during Poland’s renaissance in mathematics and philosophy in the remarkable interwar period of Polish independence. His teachers at the University of Warsaw included Stanisław Le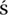 niewski and Jan Łukasiewicz in logic, SIERPI
niewski and Jan Łukasiewicz in logic, SIERPI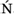 SKI [VI.77] in set theory, and Stefan Mazurkiewicz and Kazimierz Kuratowski in topology. In his thesis Tarski solved a core problem in Le
SKI [VI.77] in set theory, and Stefan Mazurkiewicz and Kazimierz Kuratowski in topology. In his thesis Tarski solved a core problem in Le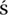 niewski’s idiosyncratic system for the foundation of mathematics, but afterward he focused on set theory and more mainstream mathematical logic. Almost immediately he obtained the spectacular BANACH–TARSKI PARADOX [V.3] (that it is possible to dissect a solid sphere into a finite number of pieces that may then be reassembled to form two spheres of the same radius as the original one) in collaboration with BANACH [VI.84].
niewski’s idiosyncratic system for the foundation of mathematics, but afterward he focused on set theory and more mainstream mathematical logic. Almost immediately he obtained the spectacular BANACH–TARSKI PARADOX [V.3] (that it is possible to dissect a solid sphere into a finite number of pieces that may then be reassembled to form two spheres of the same radius as the original one) in collaboration with BANACH [VI.84].
Encouraged by his professors, he changed his original surname, Teitelbaum, to Tarski just before receiving his Ph.D. in 1924, because a Jewish name was a professional handicap. This accorded with Tarski’s strong identification with Polish nationalism and his belief that assimilation was a rational solution to the Jewish question.
By 1930, Tarski had established one of his most important results: the completeness and decidability of formal systems of the algebra of real numbers and of Euclidean geometry axiomatized within first-order logic (see LOGIC AND MODEL THEORY [IV.23 §4]). In the following years Tarski concentrated on fundamental conceptual developments in metamathematics and the semantics of formalized languages. In contrast with HILBERT [VI.63], who called for the execution of his metamathematical consistency program by the most restricted means possible, Tarski was open to the use of any mathematical methods, including all those of set theory. His main conceptual contribution was to provide a theory of truth for formalized languages, in which he laid down a novel criterion—called the T-scheme—for an adequate definition of truth for such a language, and showed how it can be met by a set-theoretical definition within a metalanguage, while it cannot be defined within the language itself.
Though Tarski’s preeminence in Polish logic was widely acknowledged, he never succeeded in obtaining a chair in his country of birth, partly because of the paucity of positions, and partly as a result of anti- Semitism, notwithstanding his change of name. Made a Docent at the University of Warsaw as soon as he had finished his Ph.D., his position was later raised to that of Adjunct Professor. Neither post paid a living wage, and so, in order to make ends meet, Tarski also taught in a Gymnasium (high school) throughout the 1930s. Because he did not hold a chair, he could not be designated the official director of the dissertation of his first student, Andrzej Mostowski; instead Kuratowski assumed that role.
An invitation to attend a Unity of Science meeting (an offshoot of the Vienna Circle) at Harvard brought Tarski to the United States two weeks before the Nazi invasion of Poland on September 1, 1939. Given his Jewish origins, this probably saved his life, but the war separated him from his family. (His wife and immediate family survived the war, but most of the rest of his family perished in the Holocaust.) In the United States he was granted a permanent nonquota visa within months, but only temporary positions were available to him during the period 1939–42. Finally, he succeeded in obtaining a position as Lecturer in the Department of Mathematics of the University of California at Berkeley. There Tarski’s manifest excellence was soon recognized and he rose rapidly to the position of Full Professor by 1946. In the following decade, through his charismatic teaching and zealous campaigning for additional appointments in the field, he built a program in logic and the foundations of mathematics that made Berkeley a mecca for logicians from all over the world for years to come.
It was not until 1939 that Tarski wrote up his decision procedure for algebra and geometry for publication; it was slated to appear as a monograph for a Parisian publisher, but that was aborted following the invasion of France by Germany in 1940. A revised version with full details was finally prepared with the assistance of J. C. C. McKinsey as a RAND Corporation report in 1948; it only became publicly available a few years later through the University of California Press. This work then became paradigmatic for the applications of model theory to algebra in which the Tarski school led the way; the subject has continued to be one of the most important parts of mathematical logic to this day. At Berkeley during the postwar period Tarski also promoted substantial developments along several different lines: algebraic logic, the axiomatics of set theory and the significance of LARGE CARDINAL [IV.22 §6] assumptions for mathematical problems, and the axiomatics of geometry. Above all, the importance of Tarski’s work lay in opening the field of logic to the unrestricted use of set-theoretical methods, combined with a constant attention to rigorous and proper conceptual development.
Further Reading
Feferman, A. B., and S. Feferman. 2004. Alfred Tarski. Life and Logic. New York: Cambridge University Press.
Givant, S. 1999. Unifying threads in Alfred Tarski’s work. Mathematics Intelligencer 13(3):16–32.
Tarski, A. 1986. Collected Papers, four volumes. Basel: Birkhäuser.
Anita Burdman Feferman and Solomon Feferman
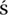 niewski and Jan Łukasiewicz in logic, SIERPI
niewski and Jan Łukasiewicz in logic, SIERPI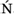 SKI [VI.77] in set theory, and Stefan Mazurkiewicz and Kazimierz Kuratowski in topology. In his thesis Tarski solved a core problem in Le
SKI [VI.77] in set theory, and Stefan Mazurkiewicz and Kazimierz Kuratowski in topology. In his thesis Tarski solved a core problem in Le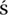 niewski’s idiosyncratic system for the foundation of mathematics, but afterward he focused on set theory and more mainstream mathematical logic. Almost immediately he obtained the spectacular BANACH–TARSKI PARADOX [V.3] (that it is possible to dissect a solid sphere into a finite number of pieces that may then be reassembled to form two spheres of the same radius as the original one) in collaboration with BANACH [VI.84].
niewski’s idiosyncratic system for the foundation of mathematics, but afterward he focused on set theory and more mainstream mathematical logic. Almost immediately he obtained the spectacular BANACH–TARSKI PARADOX [V.3] (that it is possible to dissect a solid sphere into a finite number of pieces that may then be reassembled to form two spheres of the same radius as the original one) in collaboration with BANACH [VI.84].