
We are all familiar with congested roads, and perhaps also with congestion in other networks such as the Internet, so it is obviously important to have a general understanding of how and why congestion occurs in networks. However, the pattern of the flow of traffic through a network is the consequence of a subtle and complex interaction between different users. For example, in a road network we would normally expect each driver to attempt to choose the most convenient route, and this choice will depend upon the delays the driver expects to encounter on different roads; but these delays will in turn depend upon the choices of routes made by others. This mutual interdependence makes it difficult to predict the effects of changes to the system, such as the construction of a new road or the introduction of tolls in certain places.
Related issues arise in other large-scale systems like the telephone network or the Internet. In these systems a major practical concern is the extent to which control can be decentralized. When you are browsing the Web, the rate at which a Web page is transferred to you across the network is controlled by software protocols running on your computer and on the Web server hosting the Web page, and not by some huge central computer. This decentralized approach to flow control has been outstandingly successful as the Internet has evolved from a small-scale research network to today’s interconnection of hundreds of millions of hosts, but is beginning to show signs of strain. In developing new protocols, the challenge is to understand just which aspects of decentralized flow control are important if the network as a whole is to continue to expand and evolve.
In this article we introduce the reader to some of the mathematical models that have been used to address these issues. The models need to be able to represent several distinct aspects of the system. We shall see that the language of GRAPH THEORY [III.34] and MATRICES [I.3 §4.2] is needed to capture the pattern of connections within the network. Calculus is needed to describe how congestion depends upon traffic volumes. And optimization concepts are needed to model the way in which self-interested drivers choose their shortest routes, or the way that decentralized controls in communication networks can cause the system as a whole to perform well.
figure 1 illustrates a set of three nodes connected by a set of five directed links. We might imagine the nodes as representing towns or locations within a city, and the links as representing road capacity between different nodes. A two-way road is represented by two links, one in each direction. Notice that there are two routes from node c to node a that a driver can choose: the first route, let us call it ca1, is the direct route, using link 5; the second route, let us call it ca2, is via node b and uses links 4 and 2.
Figure 1 A simple network and its link-route incidence matrix, A. The matrix H represents which routes serve which source-destination pairs.
Let J be the set of directed links and let R be the set of possible routes. One way to describe the relationship between links and routes is with a table, or matrix, defined as follows. Set Ajr = 1 if link j lies on route r, and set Ajr = 0 otherwise. This defines a matrix A = (Ajr, j ∈ J, r ∈ R) called the link-route incidence matrix. Each column of the matrix corresponds to one of the routes r, and each row to one of the links j of the network. The column for route r is composed of 0s and 1s: the 1s tell us which links are on route r. As for the rows, the 1s in the row for link j tell us which routes pass through that link. Thus, for example, the incidence matrix in figure 1 has a column for each of the two routes, ca1 and ca2, between node c and node a. These columns encode the information that route ca1 uses link 5 and that route ca2 uses links 4 and 2. Note that the incidence matrix does not tell us the order of the links on the route. Also the incidence matrix shown does not include all logically possible routes, but it could if we wanted it to. And while we have illustrated a very small network, there is no limit to the number of nodes and links there could be in the network, or to the number of choices of route each driver might have—the incidence matrix would just be bigger.
Figure 2 The time taken to travel along a link, D(y), expressed as a function of the total flow y along the link. As the flow increases, congestion effects cause additional delay.
One quantity of interest in a network is the volume of traffic along a particular route or link. Let xr be the flow on route r, defined as the number of cars per hour that travel along that route. We can list the flows along all the routes in the network as a sequence of numbers x = (xr, r ∈ R), and we can think of this sequence as a vector. From this vector we can calculate the total flow through a link: for example, the total flow through link 5 in figure 1 is the sum of the flows along routes ca1 and cb2, since these are the routes that pass through link 5. In general, since Ajr = 1 when a route r passes through link j and Ajr = 0 when it does not, the total flow through link j, coming from all of the routes that use it, is
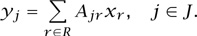
Again, the numbers (yj, j ∈ J) can be thought of as forming a vector. The above equations can then be represented succinctly in matrix form as
y = Ax.
We expect the level of congestion at a link to depend on the total flow through the link, and we expect this to influence the time taken to travel along the link. We shall call this time the delay. figure 2 shows a typical way in which the delay might depend on the amount of flow. At small values of the flow y the delay D(y) is just the time taken to travel along an empty road; for larger values of y the delay D(y) is larger, and quite possibly much larger, owing to congestion effects.1
Let Dj(yj) be the delay along link j when the flow through that link is yj; the nature of this delay may depend upon characteristics of link j such as its length and width, so we have to use the subscript j on the function Dj to indicate that the functions for the various links can be different.
Given two nodes in a network there will in general be a variety of possible routes capable of linking them. For example, in figure 1 we have seen that the incidence matrix A records two routes between nodes c and a. The pair ca is an example of a source-destination pair. Flow originating from source c and destined for node a can use either ca1 or ca2, the two routes that serve this source-destination pair. We now need another matrix, this time to describe the relationship between source-destination pairs and routes. Let us use s to denote a typical source-destination pair, and let S be the set of all source-destination pairs. Then, for each source-destination pair s and each route r, let Hsr = 1 if s can be served by the route r, and let Hsr = 0 otherwise. This defines a matrix H = (Hsr s ∈ S, r ∈ R); figure 1 gives an example. Observe that the row labeled ca has 1s for the two routes, r = ca1, ca2, that serve the source-destination pair s = ca. Each column of H corresponds to a route, and contains a single 1: this identifies the source-destination pair served by the route. For each route r let us write s(r) for the source-destination pair served by r: for example, in figure 1, s (ac) = ac and s (ca1) = ca.
From the vector x = (xr, r ∈ R) we can calculate the total flow from a source to a destination: for example, the flow from node c to node a in figure 1 is the sum of flows along routes ca1 and ca2, since from the matrix H we see that these are the routes that serve the source-destination pair ca. More generally, if fS is the total flow of traffic added up over all of the routes serving source-destination pair s, then
Thus the vector f = (fs, s ∈ S) of source-destination flows can be expressed succinctly in matrix form as f = Hx.
We are now able to approach the central issue: how do the traffic flows between the various sources and destinations distribute themselves over the links of the network? Each driver will try to use whatever route is quickest, but this may make other routes quicker or slower and cause other drivers to change their routes. Only when they cannot find alternative, quicker routes will drivers not have an incentive to change routes. What does this mean mathematically?
Let us first calculate the time taken for a driver to travel along route r. The column labeled r of the matrix A tells us which links j are on route r. If we add up the delays on each of these links, we get the time taken to travel along route r as the expression
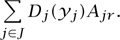
Now the driver using route r could have used any other route that served the same source-destination pair s(r). So, for the driver to be content with route r, we require
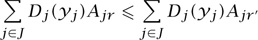
for every other route r′ that serves the same source-destination pair s(r).
Define a Wardrop equilibrium (Wardrop 1952) to be a vector x = (xr, r ∈ R) of nonnegative numbers such that for every pair of routes r, r′ serving the same source-destination pair,
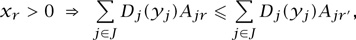
where y = Ax. The inequality expresses the defining characteristic of a Wardrop equilibrium: that if a route r is actively used, then it achieves the minimum delay over all routes serving its source-destination pair s(r).
Does a Wardrop equilibrium exist? It is not at all clear whether it is possible to find a vector x such that all of the above inequalities, for the various routes through the network, are satisfied simultaneously. To answer the question, we shall proceed by addressing a seemingly different question: what is the answer to the following optimization problem?
Minimize 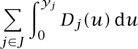
over x 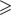 0, y,
0, y,
subject to Hx= f, Ax = y.
Let us see in outline why this optimization problem has a solution (x,y), and why, if (x,y) is a solution, the vector x is a Wardrop equilibrium.
The optimization problem has some aspects that are quite natural. An obvious constraint is that the flows along each route are nonnegative, which is why we insist that x 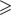 0. The constraints Hx = f, Ax = y just enforce the accounting rules we have seen earlier—the rules that allow the source-destination flows f and the link flows y to be calculated from the route flows x using the matrices H and A, respectively. We view the source-destination flows f as fixed, to be distributed over the various routes. Given a choice of f, our task is then to find the route flows x and consequently the link flows y. At a solution to the optimization problem y will be nonnegative, since x is.
0. The constraints Hx = f, Ax = y just enforce the accounting rules we have seen earlier—the rules that allow the source-destination flows f and the link flows y to be calculated from the route flows x using the matrices H and A, respectively. We view the source-destination flows f as fixed, to be distributed over the various routes. Given a choice of f, our task is then to find the route flows x and consequently the link flows y. At a solution to the optimization problem y will be nonnegative, since x is.
This much is fairly natural, but the function to be minimized looks somewhat strange. Its importance rests on the fact that the rate of change of the integral
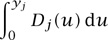
with respect to yj is Dj(yj), by THE FUNDAMENTAL THEOREM OF CALCULUS [I.3 §5.5], and the function to be minimized is the sum of these integrals over all links. We shall see that the link between Wardrop equilibria and the optimization problem is a direct consequence of this observation.
To find a solution to the optimization problem, we will use the method of LAGRANGE MULTIPLIERS [III.64]. Define the function
L(x, y, λ, μ)
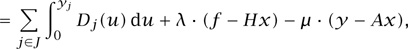
where λ = (λs, s ∈ S), μ = (μj, j ∈ J) are vectors of Lagrange multipliers, to be fixed later. The idea is that if we make the right choices of Lagrange multipliers, the minimization of the function L over x and y will find a solution to the original problem. The reason this works is that, for the right choices of Lagrange multipliers, the constraints Hx = f and Ax = y are consistent with the minimization of L.
To minimize the function L we need to differentiate.
First,

Second,
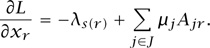
Note that the form of the matrix H causes the derivative with respect to xr to pick out exactly one component of λ, namely λs(r) and the form of the matrix A causes the derivative to pick out just those components of μ that correspond to links on route r. These derivatives allow us to deduce that a minimum of L, over all x  0 and all y, occurs when
0 and all y, occurs when
μj = Dj(yj)
and
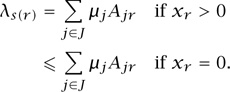
The equality condition for λs(r) is straightforward: if xr 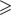 0 then small variations up or down in xr should not decrease the function L(x, y; λ, μ), and hence we deduce that the partial derivative with respect to xr must be zero. But if xr = 0 then we can only vary xr upward, and so all we can deduce is that the partial derivative with respect to xr is nonnegative, and from this we deduce the inequality condition for λs(r).
0 then small variations up or down in xr should not decrease the function L(x, y; λ, μ), and hence we deduce that the partial derivative with respect to xr must be zero. But if xr = 0 then we can only vary xr upward, and so all we can deduce is that the partial derivative with respect to xr is nonnegative, and from this we deduce the inequality condition for λs(r).
Minimizing the function L corresponds to allowing the constraints Hx = f, Ax = y to be violated, but at a cost: now one charges a price λs for any shortfall of the sum Σj∈J Ajrxr below fs and a price μs for any excess of the sum Σj∈J Ajrxr over yj. From general results on convex optimization it is known that there exist Lagrange multipliers (λ, μ) and a vector (x,y) such that (x,y) minimizes L(x, y; λ, μ), satisfies the constraints Hx = f, Ax = y, and solves the original optimization problem.
Our solution for the Lagrange multipliers shows that they have a simple interpretation: μj is the delay on link j and λs is the minimum delay over all routes serving the node pair s. The various conditions established for the multipliers thus show that an optimum of the function L, known as the objective function, corresponds precisely to a Wardrop equilibrium.
Thus if traffic in the network distributes itself in accordance with the self-interested choices of drivers, the equilibrium flows (x,y) will solve an optimization problem. This result is originally due to Beckmann et al. (1956), and it provides a remarkable insight into the equilibrium patterns achieved in road traffic networks. The pattern of traffic resulting from the individual decisions of a large number of self-interested drivers behaves as if a central intelligence were directing flows to optimize a certain (rather strange) objective function.
The result does not mean that average delays in the network will be minimal: a striking illustration of this fact is provided by Braess’s paradox (Braess 1968), which we describe next.
Consider the network illustrated in figure 3(a). Cars travel from node S to node N, via either node W or node E. The total flow is 6, and the link delays Dj(y) are given next to the links in the figure. One can imagine the figure illustrating rush hour as commuters travel from the center of a city in the south to their homes in the north. Commuters learn from experience what the delays are likely to be along the eastern and western routes. The distribution of traffic shown is the Wardrop equilibrium: there is no incentive for any drivers to change their routes, since the two possible routes incur the same delay, namely (10×3)+(3+50) = 83 units of time. Now suppose that a new link is added, between nodes W and E, as shown in figure 3(b). Traffic is attracted onto the new link, since to begin with it offers a shorter journey time from the south to the north. Eventually, after everyone knows about the new link and traffic patterns have settled down, a new Wardrop equilibrium will be established, and this is shown in figure 3(b). In the new equilibrium there are three routes used, which each incur the same delay, namely (10 × 4) + (2 + 50) (10 × 4)+(2+10)+(10 × 4)= 92. Thus in figure3(b) each car incurs a delay of 92, while in figure 3(a) the delay of each car was only 83. Adding the new link has increased everyone’s delay!
The explanation for this apparent paradox is as follows. At a Wardrop equilibrium each driver is using a route which, given the choices of others, gives the minimum delay over the routes available between that driver’s source and destination. But there is no intrinsic reason why this equilibrium should correspond to particularly low delays relative to what could be achieved by another flow pattern. If all drivers could be encouraged to depart from their own self-interested choices, it is quite possible that all might benefit. And in the above example, if all drivers in the second network could agree to avoid the new link, effectively converting the network back into the first network, then all would incur lower delays.
Figure 3 Braess’s paradox. The addition of a link causes everyone’s journey time to lengthen. (After Braess (1968) and Cohen (1988).)
To explore the point further, note that the product of the flow yj and the delay Dj(yj) is the delay incurred at link j per unit time, aggregated over all the vehicles using link j. Let us try to find the flow pattern that minimizes the total delay per unit time, summed over the entire network. Consider then the following problem.
Minimize 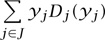
over x  0, y,
0, y,
subject to Hx = f, Ax = y.
Note that the problem is of the same form as the earlier optimization problem, but the function to be minimized now measures the total network delay per unit time. (Recall that the function to be minimized in the first optimization problem seemed initially to be rather arbitrary, with its eventual motivation being that its minimization was achieved by a Wardrop equilibrium.)
Again define the function
L(x, y; λ, μ)
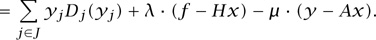
Again

but now
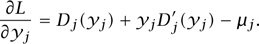
Hence a minimum of L over x 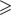 0 and y occurs when
0 and y occurs when
μj = Dj(yj) + yjD′j(yj)
and
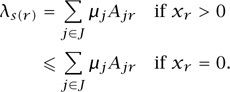
The Lagrange multipliers now have a more sophisticated interpretation. Suppose that, in addition to the delay Dj(yj), users of link j incur a traffic-dependent toll
Tj(yj) = yjD′j(yj).
Then μj is the generalized cost of using link j, defined as the sum of the toll and the delay, and λs is the minimum generalized cost over all routes serving the node pair s. If users select routes in an attempt to minimize the sum of their tolls and their delays, then they will produce a flow pattern that minimizes total delay in the network. Notice that the generalized cost μj is (∂/∂yj)(yjD(yj)), which is the rate of increase in the total delay at link j as the flow yj is increased. So the assumption now is that, in a certain sense, drivers try to minimize their contribution to the total delay rather than minimizing their own delay.
We have seen that if drivers attempt to minimize their own delay, then the resulting equilibrium flows will minimize a certain objective function defined for the network. However, the objective function is certainly not the total network delay, and thus there is no guarantee that when capacity is added to a network the situation is improved. We have also seen that, with the imposition of appropriate tolls, it is possible for the self-interested behavior of drivers to lead to an equilibrium pattern of flow that minimizes total delay. A major challenge for governments and transport planners is to understand how insights from these and more sophisticated models might be used to encourage more efficient development and use of road networks (Department for Transport 2004).
When a file is requested over the Internet, the computer that hosts that file breaks it into small packets of data that are then transferred across the network by the transmission control protocol of the Internet, or TCP. The rate at which packets enter the network is controlled by TCP, which is implemented as software on the two computers that are the source and destination of the data. The general approach is as follows (Jacobson 1988). When a link within the network becomes overloaded, one or more packets are lost; loss of a packet is taken as an indication of congestion, the destination informs the source, and the source slows down. TCP then gradually increases its sending rate until it again receives an indication of congestion. This cycle of increase and decrease enables the source computers to discover and use the available capacity, and to share it between different flows of packets.
TCP has been outstandingly successful as the Internet has evolved from a small-scale research network to today’s interconnection of hundreds of millions of endpoints and links. This in itself is a striking observation. Each of a large but indeterminate number of flows is controlled by a feedback loop that can know only of that flow’s experience of congestion. A flow does not know how many other flows are sharing a link on its route, or even how many links are on its route. The links vary in capacity by many orders of magnitude, as do the numbers of flows sharing different links. It is remarkable that so much has been achieved in such a rapidly growing and heterogeneous network with congestion controlled just at the endpoints. Why does this algorithm work so well?
In recent years theoreticians have shed some light on TCP’s success, by interpreting the protocol as a decentralized parallel algorithm that solves an optimization problem, just as the decentralized choices of drivers in a road network solve an optimization problem. We shall outline the argument, beginning with a more detailed description of TCP.2
Packets transferred by TCP across the Internet contain sequence numbers indicating their order, and they should arrive at their destination in that order. When a packet is received at the destination, it is acknowledged: an acknowledgment is a short packet sent by the destination back to the source. If a packet has been lost in the transfer, the source can tell this from the sequence numbers contained in the acknowledgments. The source keeps a copy of each packet sent until it has been positively acknowledged; these copies form what is called a sliding window, and allow packets lost in transfer to be sent again by the source.
Meanwhile, stored in the source computer there is a numerical variable known as the congestion window and denoted cwnd. The congestion window directs the size of the sliding window in the following sense: if the size of the sliding window is less than cwnd, then the computer increases it by sending out a packet; if it is greater than or equal to cwnd, then it waits for positive acknowledgments to come in, which have the effect of reducing the size of the sliding window and, as we shall see, increasing cwnd as well. Thus, the size of the sliding window continually changes, moving in the direction of a target size that is given by the congestion window.
The congestion window itself is not a fixed number: rather, it is constantly being updated, and the precise rules for how this is done are critical for TCP’s sharing of capacity. The rules currently used are as follows.
Every time a positive acknowledgment comes in, cwnd is increased by cwnd-1, and every time a lost packet is detected, cwnd is halved.3 Thus, if the source computer detects a lost packet, it realizes that there has been some congestion and backs off for a while, but if all its packets are getting through then it allows the rate at which it sends packets to inch up again.
If p is the probability that a packet is lost, then with probability 1 – p the congestion window will increase by cwnd-1 and with probability p it will decrease by  cwnd. The expected change in the congestion window cwnd per update step is therefore
cwnd. The expected change in the congestion window cwnd per update step is therefore
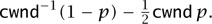
The expected change will be positive for small values of cwnd, but will become negative if cwnd is big enough. We might therefore expect an equilibrium for cwnd to arise when the expression is zero: that is, when
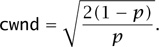
Now let us see how this calculation can be extended to networks. Suppose that a network consists of a set of nodes connected by directed links, like the network illustrated in figure 1. As earlier, let J be the set of directed links, let R be the set of routes, and let A =(Ajr, j ∈ J, r ∈ R) be the link-route incidence matrix. When a request reaches a computer in this network, that computer will set up a congestion window for the flow of packets that will result. Since there will be many different such congestion windows, they need to be labeled, and it is convenient to label them with the route that will be used for the flow. (Exactly how these flows are routed is a complicated and important question, but one that we shall not discuss here.) So, for each route r that is being used, let cwndr be the congestion window for that route. Let Tr be the round-trip time for the route r: that is, the time between the sending out of a packet and the receiving of an acknowledgment for it.4 Finally, define a variable xr to be cwndr/Tr.
Now at any given time the sliding window consists of those packets that have been sent but not acknowledged. Therefore, if a packet has just been acknowledged and its round-trip has taken time Tr, the sliding window consists of all packets sent out in the last Tr time units. Since the source computer is aiming for the number of such packets to be about cwndr, we can interpret xr to be the rate at which packets are transferred over route r. Thus, the numbers xr form a flow vector that is closely analogous to the traffic flow vector discussed earlier.
As we did then, let us define a vector y = Ax, so that yj is the total flow through link j, obtained by summing xr over each route r that passes through link j. Let pj be the proportion of packets that are lost, or “dropped,” at link j. We expect pj to be related to yj the total flow through link j, as follows. If yj is less than the capacity Cj of link j, then pj will be zero; there will be no dropped packets at link j if the link is not full. And if pj > 0 then yj = Cj: if packets are dropped then the link is full. If we assume that the proportions of packets dropped at links are small, then the probability that a packet is lost on route r is approximately
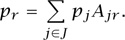
(The exact formula would be (1-pr) = ∏j∈J(1-pj)Ajr but when the pj are small we can ignore their products.) Since xr = cwndr/Tr, our earlier calculation of cwnd now gives us that
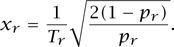
Is it possible to choose the rates x = (xr, r ∈ R) and the drop probabilities p = (pj, j ∈ J) in a consistent fashion, so that the last two equations are satisfied and either pj is zero or yj = Cj for each j ∈ J? The remarkable observation is that such a choice corresponds precisely to the solution of the following optimization problem (Kelly 2001; Low et al. 2002).
Maximize 
over x  0,
0,
subject to Ax  C.
C.
Some aspects of this optimization problem are as we might expect: in particular, the inequality Ax  C simply adds up the flows through link j and requires that the sum not exceed the capacity Cj of link j, for each link j ∈ J. But, as before, the function being optimized is undoubtedly strange. The arctan function, illustrated an objective function for the entire network. The objective function has a surprising interpretation: it is as if the usefulness of the flow rate xr to the source-destination pair served by this route is given by a utility function in figure 4, is the inverse function to the trigonometric function tan, and can also be defined as
C simply adds up the flows through link j and requires that the sum not exceed the capacity Cj of link j, for each link j ∈ J. But, as before, the function being optimized is undoubtedly strange. The arctan function, illustrated an objective function for the entire network. The objective function has a surprising interpretation: it is as if the usefulness of the flow rate xr to the source-destination pair served by this route is given by a utility function in figure 4, is the inverse function to the trigonometric function tan, and can also be defined as
Figure 4 The arctan function. The Internet’s TCP implicitly maximizes a sum of utilities over all the connections present in a network: this function shows the shape of the utility function for a single connection. The horizontal axis is proportional to the rate of the connection, and the vertical axis is proportional to the usefulness of that rate. Both axes are scaled in terms of the round-trip time of the connection.
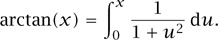
From this form, we see that its derivative with respect to x is 1/(1 + x2).
Let us sketch the relationship between the optimization problem and the equilibrium rates and drop probabilities. Define the function
L(x, z; μ)
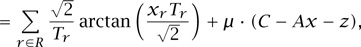
where μ = (μj, j ∈ J) is a vector of Lagrange multipliers, and z = C – Ax is a vector of slack variables, measuring the spare capacity on each of the links j ∈ J of the network. Then, using the derivative of the arctan function,
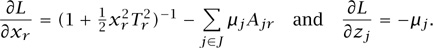
We look for a maximum of L over x, z  0; it turns out that this maximum is, under the identification μj = pj precisely the collection (xr, r ∈ R), (pj, j ∈ J) of rates and drop probabilities that we were looking for. For example, setting to zero the partial derivative with respect to xr gives the desired equation for xr.
0; it turns out that this maximum is, under the identification μj = pj precisely the collection (xr, r ∈ R), (pj, j ∈ J) of rates and drop probabilities that we were looking for. For example, setting to zero the partial derivative with respect to xr gives the desired equation for xr.
In summary, for each link j ∈ J the Lagrange multiplier μj arising from the optimization problem is precisely the proportion pj of packets dropped at that link, much as the Lagrange multipliers arising earlier were precisely the delays on links of a road traffic network. And the equilibrium reached by the interaction of many competing TCPs, each implemented only on the source and destination computers, is effectively maximizing an objective function for the entire network. The objective function has a surprising interpretation: it is as if the usefulness of the flow rate xr to the source-destination pair served by this route is given by a utility function
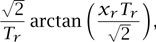
and the network is attempting to maximize the sum of these utility functions across all source-destination pairs, subject to constraints arising from the limited capacities of the links.
The arctan function, illustrated in figure 4, is concave. Thus, if two or more connections share an overloaded link, the rates achieved will be approximately equal, since otherwise the total utility could be increased by reducing the largest rate a little and increasing the smallest rate a little. As a result, there is a tendency for TCP to share resources more or less equitably. This is very different from resource-control mechanisms in traditional telephone networks where, if the network is overloaded, some calls are blocked in order that the calls that are accepted are unaffected by the overload.
The behavior of large-scale systems has been of great interest to mathematicians for over a century, with many examples coming from physics. For example, the behavior of a gas can be described at the microscopic level in terms of the position and velocity of each molecule. At this level of detail a molecule’s velocity appears as a random process, as the molecule bounces around off other molecules and the walls of the container. Yet consistent with this detailed microscopic description of the system is macroscopic behavior best described by quantities such as temperature and pressure. Similarly, the behavior of electrons in an electrical network can be described in terms of random walks, and yet this simple description at the microscopic level leads to rather sophisticated behavior at the macroscopic level: Kelvin showed that the pattern of potentials in a network of resistors is exactly the one that minimizes heat dissipation for a given level of current flow (Kelly 1991). The local, random behavior of the electrons causes the network as a whole to solve a rather complex optimization problem.
In the last fifty years we have begun to realize that large-scale engineered systems are often best understood in similar terms. Thus a microscopic description of traffic flow in terms of each driver’s choice of the most convenient route can be consistent with macroscopic behavior described in terms of a function minimization. And the simple, local rules that control how packets are transmitted through the Internet can correspond to a maximizing of aggregate utility across the entire network.
One thought-provoking difference is that, whereas the microscopic rules governing physical systems are fixed, for engineered systems such as transport or communication networks we may be able to choose the microscopic rules so as to achieve the macroscopic consequences we judge desirable.
Beckmann, M., C. B. McGuire, and C. B. Winsten. 1956. Studies in the Economics of Transportation. Cowles Commission Monograph. New Haven, CT: Yale University Press.
Braess, D. 1968. Über ein Paradoxon aus der Verkehrsplanung. Unternehmenforschung 12:258-68.
Cohen, J. E. 1988. The counterintuitive in conflict and cooperation. American Scientist 76:576-84.
Department for Transport. 2004. Feasibility study of road pricing in the UK. Available from www.dft.gov.uk.
Jacobson, V. 1988. Congestion avoidance and control. Computer Communication Review 18(4):314-29.
Kelly, F. P. 1991. Network routing. Philosophical Transactions of the Royal Society of London A 337:343-67.
——. 2001. Mathematical modeling of the Internet. In Mathematics Unlimited—2001 and Beyond, edited by B. Engquist and W. Schmid, pp. 685-702. Berlin: Springer.
Low, S. H., F. Paganini, and J. C. Doyle. 2002. Internet congestion control. IEEE Control Systems Magazine 22: 28-43.
Wardrop, J. G. 1952. Some theoretical aspects of road traffic research. Proceedings of the Institute of Civil Engineers 1: 325-78.
1. The graph shown in figure 2 is single valued. It is quite possible for the curve representing delay as a function of flow to bend back upon itself, so that higher delays than shown in the graph correspond to flows smaller than the maximum flow shown there. You are in this part of the graph when you experience stop-start driving conditions on a congested but otherwise incident-free highway. Part of the aim of traffic management is to keep flows and delays away from this part of the graph, which we will not consider further.
We will assume that the graph is increasing and smooth, which will make our use of calculus later more straightforward. Formally, we shall assume that D(y) is a continuously differentiable and strictly increasing function of its argument y, as in the graph shown in figure 2.
2. Even our detailed description of TCP is simplified, concerning just the congestion-avoidance part of the protocol and omitting discussion of timeouts or of reactions to multiple congestion indication signals received within a single round-trip time.
3. These increase and decrease rules may appear rather mysterious, and indeed it is only recently that many of their macroscopic consequences have begun to be understood. The rules have worked well for more than a decade, but they are now beginning to show signs of age, and much current research is aimed at understanding the full consequences of changing them.
4. The round-trip time comprises the time taken for a packet to travel along links, called the propagation delay, together with processing times and queueing delays at nodes. Processing times and queueing delays tend to decrease with increasing computer speeds, but the finite speed of light places a fundamental lower bound on propagation delays. We shall treat the round-trip time for a route as a constant. Hence, we assume that congestion at a link makes itself felt by packet loss rather than additional packet delay.