Cryptography is the science of hiding the meaning or content of communications. The aim is that an adversary who sees a message only in its enciphered state cannot make sense of or derive useful information from what is seen. On the other hand, the intended recipient must be able to decipher the true meaning. For most of history cryptography has been an art practiced seriously only by a few—such as governments for military and diplomatic communications—for whom the consequences of unauthorized disclosure of information are damaging enough to justify the expense and inconvenience of enciphering messages. Recently this has changed: one of the results of the information revolution has been the need for instant and secure communication for all on demand. Fortunately, mathematics has come to the rescue and provided theoretical and algorithmic developments to meet this need. It has also provided entirely new possibilities, such as “digital signatures” (which will be discussed later).
One of the oldest and most basic methods of cryptography is simple substitution. Suppose that a message to be enciphered consists of a piece of English text. Before it is sent, the sender and recipient agree on a permutation of the twenty-six letters of the alphabet, which they keep private. An enciphered message might then look something like
ZPLKKWL MFUPP UFL XA EUXMFLP
For very short messages this method is reasonably secure—it is just possible to work out the meaning of the above example by matching letter patterns to those commonly seen in English, but it is quite challenging! However, for longer messages, simply counting the frequencies of each letter and comparing those counts with the frequencies of letters in natural language will almost always reveal the hidden permutation sufficiently to allow the meaning to be easily recovered.
A major leap forward in cryptography came with the advent of mechanical encryption devices in the twentieth century, of which the German Enigma used during World War II is perhaps the most famous example. An account of the fascinating Enigma story and the role of the code breakers of Bletchley Park appears in Simon Singh’s excellent book on cryptography (Singh 1999). It is interesting that the principle on which Enigma operates is a development of the simple substitution method. Each letter of the input message is enciphered exactly as a simple substitution, but with the additional rule that the permutation controlling the substitution changes after every letter. A complex electromechanical device controls the substitution process in a deterministic way. The recipient can decipher the message only if he or she can set up another device in exactly the same way as the originator. The information needed to do this is called the key. Making sure that keys are known only by the right people is called key management. Until the advent of public-key cryptography (to be discussed later), key management was a major inconvenience and expense for anyone wanting to secure their communications.
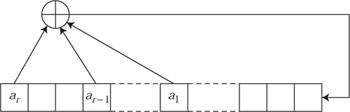
Since the advent of computers, information has tended to be transmitted as binary data: that is, as a stream of 0s and 1s. For such data there is a rather different method of encipherment based on a device called the linear feedback shift register, or LFSR (see figure 1). The first step is to generate a random-looking sequence of 0s and 1s in a deterministic way, and this is done by means of a recurrence formula, of which a simple example is
Figure 1 Linear feedback shift register.
xt = xt-3 + xt-4.
Here, addition is mod 2, so xt will be 1 if an odd number of the terms xt-3, xt-4 is 1, and it will be 0 otherwise. We must also specify the first four values of the sequence, so let us begin with 1000. The sequence then continues as follows:
100110101111000100110101111 . . . .
More generally, one specifies some positive integers a1, a2, . . . ,ar, called feedback positions—the numbers 3 and 4 in the above example—and defines a sequence by means of the recurrence formula
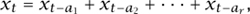
where again the addition is mod 2.
A sequence produced in this way usually looks fairly random, but because there are only finitely many binary sequences of length ar it must eventually repeat. Notice that, in our example, the sequence is periodic with period 15, which is actually the longest possible period, since there are sixteen binary sequences of length 4, and after a moment’s thought one sees that the sequence 0000 cannot occur (or else the whole sequence up to then would have had to consist entirely of zeros).
In general, the length of the sequence depends on properties of the polynomial
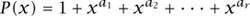
over the FIELD [I.3 §2.2]  2 of two elements. As we have just seen in the case ar = 4, the maximum possible sequence length is 2ar. – 1, and for this length to be achieved the polynomial P(x) must be irreducible over
2 of two elements. As we have just seen in the case ar = 4, the maximum possible sequence length is 2ar. – 1, and for this length to be achieved the polynomial P(x) must be irreducible over  2: that is, it must not factorize into smaller polynomials. For example, the polynomial 1 + x4 + x5 is not irreducible, because (1 + x + x3)(1 + x + x2) expands out to
2: that is, it must not factorize into smaller polynomials. For example, the polynomial 1 + x4 + x5 is not irreducible, because (1 + x + x3)(1 + x + x2) expands out to
1 + x + x + x2 + x2 + x3 + x3 + x4 + x5,
which equals 1 + x4 + x5 since 1 + 1 = 0 in the field  2.
2.
Irreducibility is a necessary condition for the sequence to have the maximum length, but it does not guarantee it. For that we need a second condition: that the polynomial is primitive. To see what this means, let us take the polynomial x3 + x + 1 and calculate the remainder when, for the first few positive integers m, we divide xm by x3 + x + 1 (with all coefficients in  2). When m goes from 1 to 7 we obtain the polynomials x, x2, x + 1, x2 + x, x2 + x + 1, x2 + 1, 1. For instance,
2). When m goes from 1 to 7 we obtain the polynomials x, x2, x + 1, x2 + x, x2 + x + 1, x2 + 1, 1. For instance,
x6 = (x3 + x + 1)(x3 + x + 1) + x2 + 1,
so the remainder on dividing x6 by x3 + x + 1 is x2 + 1.
Now the first time that we obtained the polynomial 1 was when m = 7, and 7 = 23 – 1. This shows that the polynomial x3 + x + 1 is primitive. In general, a polynomial p(x) of degree d is primitive if the first time you obtain a remainder of 1 when you divide xm by p(x) is when m = 2d – 1.
There are computationally efficient tests for determining whether a polynomial is irreducible and whether it is primitive. The advantage of using a primitive polynomial as the basis of an LFSR is that, in the sequence it generates, no subsequence of length ar is repeated until all nonzero sequences of length ar have appeared exactly once.
How is all this applied in cryptography? A simple idea would be to take the stream of bits generated by an LFSR and add it term by term to the message one is enciphering. For instance, if the LFSR generated a sequence that began 1001101 and the message was 0000111, then the encrypted message would begin 1001010. To decipher such a message, one could simply repeat the process: adding the two sequences 1001101 and 1001010 gives the original message 0000111. For this to work, the recipient would need to know the details of the LFSR in order to be able to generate the same sequence 1001101, so one might consider using the feedback positions (in this case 3 and 4) as the secret key.
The above procedure is not good enough to be of practical use because there is an efficient algorithm, due to Berlekamp and Massey (1969), that can recover the feedback rule from the stream of bits it generates. It is better to use some predetermined nonlinear function of the successive sequences of ar bits in order to scramble further the sequence of bits produced by the LFSR. Even then, such procedures are simple enough that, with careful design, they can be applied to large amounts of data very quickly.
Figure 2 Feistel round structure.
When computers started to be used, an entirely different method of cryptography became practical: the block cipher. The first example of this was DES: the Data Encryption Standard (first published in 1977). DES was adopted as a standard in 1976 by the U.S. National Bureau of Standards (now the National Institute of Standards and Technology). This enciphers a block of 64 bits at a time, with a key of length 56 bits. It has a particular structure, referred to as a Feistel cipher (see figure 2).
This structure is as follows. Given a block of 64 bits, you first divide it into two parts of 32 bits each, and call them L and R. Next, you take a subset of the 56 bits of the key, according to some predetermined rule, and use this subset to define a nonlinear function F, again according to some predetermined rule, which takes 32-bit sequences to 32-bit sequences. You then replace the pair [L,R] by the pair [R ⊕ F(L),L]. (Here R ⊕ F(L) denotes the result of taking the mod-2 sum of R and F(L) one bit at a time.)
Having done that, you repeat the process a number of times, choosing a different nonlinear function F each time (but always deriving it in a predetermined way from the 56-bit key). A complete encryption by DES consists of 16 such rounds, together with some permutation of the bits of the input and output.
One reason for using the Feistel structure is that as long as one knows the 56-bit key it is quite easy to reverse the encryption process. Given a round that performs the transformation
[L, R] → [R ⊕ F(L), L],
one can invert it by means of the transformation
[L, R] → [R, L ⊕ F(R)].
This has the great advantage that it does not require us to invert F, so even if F is quite complicated the procedure can be easy to carry out.
A number of what are called “modes of use” of DES have been developed. Simply using the algorithm to encrypt each 64-bit block of data in turn is called ECB (for electronic codebook) mode. A disadvantage of this mode is that if there is an exact 64-bit repeat in the data then this results in an exact 64-bit repeat in the cipher.
Another mode is CBC, or cipher block chaining, mode. Here, each block of data is added mod 2 to the previous block before being encrypted as above. In OFB, or output feedback, mode the block of data is added to the DES encipherment of the previous block. It is an easy exercise to see how to decipher in CBC and OFB modes, and in practice these are the two most common modes of use of DES.
The U.S. National Institute of Standards and Technology recently held a competition for a replacement for DES, to be called the Advanced Encryption Standard, or AES. This was to be a 128-wide block cipher with a variety of possible key lengths. Many competing designs were submitted and subjected to public scrutiny, and the winning entry was called Rijndael, after the designers Joan Daemen and Vincent Rijmen.
The design is remarkable and elegant and makes use of interesting mathematical structures (Daeman and Rijmen 2002). The 128 bits in each block are thought of as 16 bytes (a byte consists of eight bits), arranged in a 4 × 4 square. Each byte is then thought of as an element of  256, the field of order 256. Encryption consists of ten or more rounds (the exact number depending upon the key length); and each round mixes the data and the key.
256, the field of order 256. Encryption consists of ten or more rounds (the exact number depending upon the key length); and each round mixes the data and the key.
A round consists of a series of steps, typically as follows. First, each byte, regarded as an element of the finite field  256, is replaced by its inverse in the field, except that 0 is left unchanged. Each byte is then regarded as an element of the vector space of dimension 8 over the field
256, is replaced by its inverse in the field, except that 0 is left unchanged. Each byte is then regarded as an element of the vector space of dimension 8 over the field  2 and an invertible linear transformation is applied. Each row of the 4 × 4 square is then rotated, by a different number of bytes for each row. Next, the values of each column of the square are taken to be the coefficients of a degree 3 polynomial over
2 and an invertible linear transformation is applied. Each row of the 4 × 4 square is then rotated, by a different number of bytes for each row. Next, the values of each column of the square are taken to be the coefficients of a degree 3 polynomial over  256 and this is multiplied by a fixed polynomial and reduced modulo x4 + 1. Finally, the key for the round, which is derived linearly from the encryption key, is added modulo 2 to the 128 bits.
256 and this is multiplied by a fixed polynomial and reduced modulo x4 + 1. Finally, the key for the round, which is derived linearly from the encryption key, is added modulo 2 to the 128 bits.
It can be seen that all of these steps are reversible, which makes decipherment straightforward. It is likely that AES will take over from DES as the most widely used block cipher.
The various encryption methods described above rely on the computational difficulty of recovering some secret that protects the enciphered data. There is one classic encryption method that does not rely on this property. This is the “one-time key.” Imagine that the message to be enciphered is encoded as a sequence of bits (for example, the standard ASCII encoding that represents each character as eight bits). Suppose that ahead of time the sender and recipient have shared a sequence of random key bits r1, . . . , rn at least as long as the message. Suppose that the message bits are p1, p2, . . . , pn.
The enciphered message is then x1, x2, . . . , xn, where xi = pi + ri. Here, as usual, addition is mod 2 addition in each bit. If the bits ri are fully random, then knowing the sequence xi gives no information whatsoever about the message sequence pi. This system is called one-time key. It is very secure as long as the key is used only once. However, it is impractical to use this method except in very specialized situations because of the need for sender and recipient to share and keep safe possibly large quantities of key material.
All of the examples of encryption methods that we have seen so far have had the following structure. Two communicators agree on an algorithm or method for encryption. The choice of method (e.g., simple substitution, AES, or one-time key) can be made public without the security of the system being compromised. The two communicators also agree on a secret key in the form required by the chosen encryption method. This key needs to be kept secure and never revealed to any adversary. The communicators encipher and decipher messages using the algorithm and secret key.
This presents a major problem: how can the communicators securely share the secret key? It would be insecure to exchange this over the same system that they will later use to send enciphered messages. Until so-called public-key methods were discovered this issue limited the use of encryption to those organizations that could afford the physical security and separate communication channels necessary for distributing keys reliably.
The following remarkable, counterintuitive proposition forms the basis of public-key cryptography: it is possible for two entities to communicate information in such a way that they start with no secret shared information; an adversary has access to all communications between them; at the end the entities have shared secret knowledge that the adversary is unable to determine.
It is easy to see how useful such a capability could be. Consider, for example, someone making a purchase over the Internet. Having identified a product one wishes to buy the next step is to send personal information such as credit card details to the vendor. With public-key cryptography it is possible to do this in a secure manner straightaway.
How might public-key cryptography be possible? The structure of a solution was proposed by James Ellis in 1969,1 with the first public description by Diffie and Hellman (1976). The critical idea is to use a function that is hard to invert unless you have an “inverse key” that helps you to do so.
More formally, a one-way function H is a mapping from a set X to itself, with the property that if you are told the value y = H(x) for some x ∈ X, then it is computationally hard to determine x. The inverse key is a secret value, z, say, used in creating the function H, with the property that if you know z then it becomes computationally easy to recover x from H(x).
We can use this to solve the problem of secure key exchange as follows. Let us suppose that Bob wishes to send some data securely to Alice. (Particularly useful would be a shared secret that they can use later as a key for subsequent communications.) Alice begins by generating a one-way function H with an inverse key z. She then communicates the function H to Bob, but the inverse key remains her personal secret, which she reveals to no one—not even to Bob. Bob takes the data x that he wishes to send, computes H(x), and returns the result of his computation to Alice. Because Alice has the inverse key z, she can reverse the function H and thereby recover x.
Now suppose that an adversary manages to read all the communications between Alice and Bob. Then the adversary will know the function H and the value H(x). However, Alice has not communicated the inverse key z, so the adversary is faced with the computationally intractable problem of inverting H. Therefore, Bob has successfully transmitted the secret x to Alice without the adversary being able to work out what it is. (For a more precise idea of what computational intractability is and a further discussion of one-way functions, see COMPUTATIONAL COMPLEXITY [IV.20], especially section 7.)
It can be helpful to imagine the one-way function H as a padlock and the inverse key as the key that unlocks the padlock. Then if Alice wants to receive an enciphered message from Bob, she sends him her padlock, retaining the key. Bob locks (enciphers) the message into a box with the padlock, and returns it. Only Alice, who is in possession of the padlock key, can unlock (decipher) the message.
It is all very well to have such a framework, but it leaves open an obvious question: how can one produce a one-way function with an inverse key? The following method was published by Rivest, Shamir, and Adleman (1978). It relies on the fact that it is relatively easy to find large prime numbers and multiply them to produce a composite number, but it is much harder, if you are given that composite number, to determine its two prime factors.
To create a one-way function by their method, Alice first finds two large prime numbers P and Q. She then calculates the integer N = PQ and sends it to Bob, together with another integer e called the encryption exponent. The values N and e are called the public parameters because it does not matter if an adversary knows what they are.
Bob then expresses the secret value x that he wishes to send to Alice as a number modulo N. Next, he computes H(x), which is defined to be xe mod N, that is, the remainder when xe is divided by N. Bob sends H(x) to Alice.
Upon receipt of Bob’s message, Alice needs to recover x from xe mod N. This she can do by first calculating the number d that satisfies the equation
de ≡ 1 mod (P − 1)(Q − 1).
To do this efficiently, Alice can use EUCLID’S ALGORITHM [III.22]. Notice, however, that this would not be possible if she did not know the values of P and Q. In fact, the ability to calculate the correct value of d can be shown to be equivalent to the ability to factorize N. The value of d is Alice’s private key (or “inverse key” in the terminology above): it is the secret that can undo the encryption function H.
This is because H(x)d mod N can be shown to equal x. Indeed, the significance of the number (P − 1)(Q − 1) is that it equals φ(N), the number of integers less than N and coprime to N. EULER’S THEOREM [III.58] states that xφ(N) ≡ 1 mod N whenever x is coprime to N. Therefore, xmφ(N) ≡ 1 mod N as well, so if de has the form mφ(N) + 1, as we are assuming, then H(x)d xde ≡ x mod N. In other words, if you raise x to the power e mod N and then raise that to the power d mod N you get back to x. (An important point is that raising numbers to powers mod N is computationally easy by the method of “repeated squaring.” This is discussed in COMPUTATIONAL NUMBER THEORY [IV.3 §2].)
While it has not been proved that the only way for an adversary to defeat the RSA encryption system is to factorize N, no other general attack has been found. This has created interest in finding improved factorization methods. A number of new subexponential methods—elliptic curve factorization (Lenstra 1987), the multiple polynomial quadratic sieve (Silverman 1987), and the number field sieve (Lenstra and Lenstra 1993)—have been discovered in the years since the RSA algorithm was found. See COMPUTATIONAL NUMBER THEORY [IV.3 §3] for discussions of some of them.
The security of the RSA system depends on the primes P and Q being large enough to make factorization hard. However, the larger they are, the slower the encryption process is. Thus, there is a trade-off between security and the speed of encryption. A typical choice that is often made is to use primes that are each of 512 bits.
For the deciphering method to work, the encryption exponent e must have no factors in common with either (P − 1) or (Q − 1). This assumption was needed when we applied Euler’s theorem, and if it does not hold then the encryption function is not invertible. Values such as 17 or 216 + 1 are often used in practice, because making e small reduces the amount of computation needed to calculate the encrypted value xe mod N. (These two values of e are also well-suited to calculation by repeated squaring.)
Another approach to generating a shared secret was published by Whitfield Diffie and Martin Hellman. In their protocol Alice and Bob jointly create a shared secret, which can then be used as the key for one of the conventional cryptographic systems such as AES. To do this, they agree on a large prime number P and a primitive element g modulo P, which means a number g such that gP − 1 ≡ 1 mod P, but gm 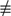 1 mod P for any m <P−1.
1 mod P for any m <P−1.
Alice then creates her own private key a, a number randomly chosen between 1 and P − 1, and calculates ga = ga mod P and sends this to Bob.
Bob similarly creates his own private key b between 1 and P − 1 and calculates and sends gb = gb mod P to Alice.
Alice and Bob can now create the shared secret gab mod P. Alice calculates this as 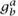 mod P and Bob calculates this as
mod P and Bob calculates this as 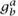 mod P. Note that all of these terms can be calculated in time logarithmic in a and b through repeated squaring.
mod P. Note that all of these terms can be calculated in time logarithmic in a and b through repeated squaring.
An adversary, however, would see only ga mod P and gb mod P, and would also know g and P. How could 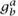 mod P be determined from this? One method is to solve what is called the discrete logarithm problem. This is the problem of calculating a if you know P, g, and ga mod P. For large P this appears to be a computationally intractable problem. It is not known for certain whether there is a faster way for the adversary to calculate
mod P be determined from this? One method is to solve what is called the discrete logarithm problem. This is the problem of calculating a if you know P, g, and ga mod P. For large P this appears to be a computationally intractable problem. It is not known for certain whether there is a faster way for the adversary to calculate 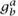 mod P than computing discrete logarithms—this is called the Diffie-Hellman problem—but at present no better method is known.
mod P than computing discrete logarithms—this is called the Diffie-Hellman problem—but at present no better method is known.
It is not obvious how to find primitive elements in general, but it is much easier if, as is usually the case, the prime P has been constructed so as to ensure that the factorization of P − 1 is known. For instance, if P is of the form 2Q + 1, where Q is also a prime (such numbers are called Sophie Germain primes), then it can be shown that for any a, exactly one of a and −a has the property that its Qth power is congruent to −1 mod P, and this one is a primitive element. In practice, one can find such primes by a process of trial and error: for example, one can choose a number Q randomly and use randomized primality tests to see whether Q and 2Q + 1 are prime. Assuming that, as everyone believes, such pairs occur with the “expected” frequency, the probability of finding one on any given attempt is large enough for this approach to be feasible.
The Diffie-Hellman protocol can be expressed in the language of GROUP THEORY [I.3 §2.1]. Suppose we have a group G and some element g ∈ G. We will require the group to be Abelian and will use “+” to denote the group operation. (In the examples so far, the groups under consideration were multiplicative groups consisting of elements coprime to some integer N, so by using additive notation we are taking a “logarithmic” perspective.)
To execute the protocol Alice computes some private integer a and computes and sends ag to Bob. Note that Alice can compute this sum of a elements of G in time of order logarithmic in a by successive doubling and adding. (In the multiplicative groups considered earlier, “doubling” is squaring, “adding” is multiplying, and “multiplying by a” is raising to the power a.)
Similarly, Bob computes a private integer b and computes and sends bg to Alice.
Both Alice and Bob can calculate the shared value abg. An adversary will know only G, g, ag, and bg.
The question is: which groups can be used in practical cryptographic systems? The critical property is that the discrete logarithm problem in G must be hard; in other words, given G, g, and ag it should be a hard problem to determine a.
One type of group that has aroused interest for cryptographic purposes is the additive group generated by points on an ELLIPTIC CURVE [III.21]. An elliptic curve has an equation of the form
y2 = x3 +ax + b.
It is an interesting exercise to sketch this curve over the real numbers—the shape depends upon how many times the curve
y = x3 + ax + b
crosses the x-axis.
It is possible to define an “addition rule” (often called a group law) on the points of this curve, as follows. Given two points A and B on the curve, the straight line joining them must meet the curve in a third point, C say. This is because a straight line must meet a cubic in three places precisely. Define A + B to be the mirror image of C in the x-axis (see figure 3).
It is obvious that A + B = B + A from this definition. What is rather more surprising is that the associative law holds. That is, for any three points A, B, and C we have ((A + B) + C) = (A +(B + C)). There are some deep reasons why this is true, but of course it can be verified by just doing the algebra.
To use this for cryptography the group is formed from the set of points on an elliptic curve defined over a finite field. The graphical image for the sum of two points is no longer valid, but the algebraic definition still holds, so addition still obeys the associative law. We need to add one further point to the set of points on the curve to function as the zero of the group: this is the “point at infinity” on the curve.
Figure 3 Addition of points on an elliptic curve.
For optimal security it turns out to be best to find a curve defined over  p for which the number of elements in the group is a prime number. In fact it is guaranteed—by a deep result on the theory of elliptic curves—that the number of points on a curve defined over
p for which the number of elements in the group is a prime number. In fact it is guaranteed—by a deep result on the theory of elliptic curves—that the number of points on a curve defined over  p will lie between p + 1 − 2
p will lie between p + 1 − 2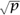 and p + 1 + 2
and p + 1 + 2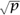 . (See THE WEIL CONJECTURES [ν.35].)
. (See THE WEIL CONJECTURES [ν.35].)
The reason this group is used is that for general curves the discrete logarithm problem appears to be particularly hard. If the group has n elements and if we are given group elements g and ag, then the number of steps needed to determine a, by the best algorithms that are currently known, is around 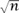 Since there is a so-called birthday attack that allows one to solve this problem in any group with n elements in around
Since there is a so-called birthday attack that allows one to solve this problem in any group with n elements in around 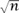 computational steps, this means that the problem for elliptic curve groups is as hard as it can be. Therefore, whatever level of security you require, the public key is as short as it can be. This is important when there are constraints on the number of bits that can be sent as it allows the protocol to be executed in the minimum possible time.
computational steps, this means that the problem for elliptic curve groups is as hard as it can be. Therefore, whatever level of security you require, the public key is as short as it can be. This is important when there are constraints on the number of bits that can be sent as it allows the protocol to be executed in the minimum possible time.
As well as secure transmission of data, there is another very useful capability that is provided by public-key cryptography. That is the concept of a digital signature. A digital signature is a string of symbols that an author attaches to the end of a message that certifies the authenticity of the message. In other words, it proves that the message was written by the attested author and that it has not been modified. Once the necessary frameworks are in place, this opens up the possibility of much legal business being conducted online.
There are a number of ways that public-key methods can be used to create digital signatures. The one based on the RSA system is perhaps the simplest. Suppose Alice wants to sign documents. Just as she does for encryption, she generates two large prime numbers P and Q and calculates her public modulus N = PQ and her public exponent e. She also generates her private key—the deciphering exponent d with the property that xde ≡ x mod N for any x. She will use the same parameters both for encryption and for the creation of digital signatures.
Alice can assume that the recipients of her signed messages know her N and e values. In practice she may have these values themselves signed and certified by a trusted authority or organization that the prospective recipient of a signed message will recognize.
One other component of this system is an object called a one-way hash function, which takes as its input the message to be signed, which may be rather long, and outputs a number between 1 and N − 1. The important property that a hash function must have is that for any value y between 1 and N it is computationally hard to construct a message x that hashes to that value. This is similar to a one-way function except that we are no longer assuming that for each y there is exactly one x that maps to y. However, the hash function should ideally also be collision free, which means that, even though there are many pairs of messages that hash to the same value, it is not easy to find any. Such hash functions need to be carefully designed, but there are some recognized standard hash functions (two of which are called MD5 and SHA-1). Suppose that x is the message to be signed, and let X be the output when you apply the hash function to x. The digital signature that Alice appends to the message is Y = Xd mod N.
Observe that anyone in possession of Alice’s public key can verify the signature by following these steps. First, calculate the hashed value X of the message x, which is possible because the hash function is made public. Next, compute Z = Ye mod N, which can be done because the parameters N and e are also public. Finally, verify that X equals Z. In order to fake such a signature, you have to find Y with the property that Ye ≡ X mod N. That is, you must know how to calculate Xd, which is computationally intractable if you do not already know d.
It is also possible to construct digital signatures using a public key based on discrete logarithms (Diffie-Hellman type) rather than on factorization (RSA type). The U.S. standards body has published such a proposal: the Digital Signature Standard (1994).
Cryptography remains an active and fascinating area for research—there are undoubtedly more results and ideas to be discovered. For a good overview of current activity one should look at recent proceedings of the main conferences, such as Crypto, Eurocrypt, or Asia- crypt (these are published in the Springer series Lecture Notes in Computer Science). The comprehensive book on cryptography by Menezes, van Oorschott, and Van-stone (1996) is a good way to get up to speed on present theory. In this final section I outline just a few of the directions in which the subject is moving.
One important area of investigation is the search for new public-key methods and signature schemes. Recently some interesting new ideas have come from the use of pairings on elliptic curves (Boneh and Franklin 2001). These are maps w from pairs of points on the curve to either the finite field over which the curve is defined or an extension field.
A pairing w is bilinear, in the sense that w (A+B, C) w (A, C) w (B, C) and w (A, B + C) = w (A, B) w (A, C), where addition is the group operation defined on points of the curve and multiplication takes place in the field.
One way that such a map can be used is to create an “identity-based cryptosystem.” Here, a user’s identity serves as his or her public key, which eliminates the need for directories or other public-key infrastructure in order to store and propagate public keys.
In such a system, a central authority decides upon a curve, a pairing map w, and a hash function that maps identities to points on the curve. All of this is made public, but there is also a secret parameter, an integer x.
Suppose that the hash function maps Alice’s identity to the point A on the curve. The authority calculates Alice’s private key xA and issues it to her when she registers, after making appropriate checks on her identity. Similarly, Bob would receive his private key xB, where B is the point on the curve corresponding to his identity.
Alice and Bob are now able to communicate without any initial key exchange, using the common key w (xA, B) = w (A, xB). The important point is that unlike other public-key systems this can be done without any need to share public keys.
A second area of activity is the study of proposed protocols, especially those likely to become international standards. When public-key methods are to be used in practical communication the sequence of bits to be transmitted needs to be clearly defined, so that both communicating parties understand the same thing by each bit sent. For example, if an n-bit number is transmitted, are the bits transmitted in increasing or decreasing order of significance? The rules or protocols are often enshrined in public standards, and it is important that they do not introduce any weakness into the system.
An example of the sort of weakness that can be introduced in this way is one discovered by Coppersmith (1997) in a seminal paper. He showed that in a low-exponent RSA system (for example, one with encryption exponent equal to 17) a weakness arises if too many of the bits of the number that is to be enciphered are set to publicly known values. This is something that is natural to want to do, if, as is often the case, a large public-key modulus is being used to transmit a much shorter communication key. As a result of Coppersmith’s discovery such fields are nowadays usually padded out before they are encrypted, with bits that vary unpredictably.
Using public-key methods, one can control very precisely how information is released, shared, or generated. Research in this area is usually focused on finding elegant and efficient ways of achieving different sorts of control in a variety of situations. As a simple example, we might want to create a secret that is shared between N people in such a way that if any K people combine their share (where K < N) they can reconstruct the secret, but no information can be gained about the secret by any smaller number than K collaborating.
Another example of this type of control is a protocol that allows two participants to create an RSA modulus (a product of two primes) in such a way that neither participant gets to know the primes that were used to produce the modulus. To decipher a message enciphered under this modulus the two participants have to collaborate—neither can achieve this on their own (Cocks 1997).
A third and more amusing example is a protocol that allows Alice and Bob to replicate tossing a coin, but to do it over the telephone. Obviously, it would not be satisfactory for Alice to toss the coin and for Bob to make the call “heads” or “tails”—for how does Bob know that Alice is telling the truth about how the coin actually fell? This problem turns out to have a simple solution. Alice and Bob choose large random sequences. Alice then appends either a 1 or a 0 to her sequence and Bob does the same for his. Alice’s extra bit represents the outcome of the coin toss, and Bob’s represents his guess. Next, they send one-way hashes of their sequences (with the extra bits appended). At this point, because of the nature of one-way hashes, neither has any idea what the other’s sequence is, so, for example, if Alice reveals her hashed sequence first, Bob cannot use this information to increase his chance of guessing correctly. Alice and Bob then exchange the unhashed sequences to see whether Bob’s guess was correct. If either does not trust the other, they can hash the other’s sequence to check that it really does give the right answer. Since it is hard to find a different sequence that gives the right answer, they can each be confident that the other has not cheated. More complicated protocols of this type have been designed—it is even possible to play poker remotely in this way.
Boneh, D., and M. Franklin. 2001. Identity-based encryption from the Weil pairing. In Advances in Cryptology—CRYPTO 2001. Lecture Notes in Computer Science, volume 2139, pp. 213-29. New York: Springer.
Cocks, C. 1997. Split Knowledge Generation of RSA Parameters. Cryptography and Coding. Lecture Notes in Computer Science, volume 1355, pp. 89-95. New York: Springer.
Coppersmith, D. 1997. Small solutions to polynomial equations, and low exponent RSA vulnerabilities. Journal of Cryptology 10(4):233-60.
Daeman, J., and V. Rijmen. 2002. The Design of Rijndael. AES—The Advanced Encryption Standard Series. New York: Springer.
Data Encryption Standard. 1999. Federal Information Processing Standards Publications, number 46-3.
Diffie, W., and M. Hellman. 1976. New directions in cryptography. IEEE Transactions on Information Theory 22(6): 644-54.
Digital Signature Standard. 1994. Federal Information Processing Standards Publications, number 186.
Lenstra, A., and H. Lenstra Jr. 1993. The Development of the Number Field Sieve. Lecture Notes in Mathematics, volume 1554. New York: Springer.
Lenstra Jr., H. 1987. Factoring integers with elliptic curves. Annals of Mathematics 126:649-73.
Massey, J. 1969. Shift-register synthesis and BCH decoding. IEEE Transactions on Information Theory 15:122-27.
Menezes, A., P. van Oorschott, and S. Vanstone. 1996. Applied Cryptography. Boca Raton, FL: CRC Press.
Rivest, R., A. Shamir, and L. Adleman. 1978. A method for obtaining digital signatures and public-key cryptosystems. Communications of the Association for Computing Machinery 21(2):120-26.
Silverman, R. 1987. The multiple polynomial quadratic sieve. Mathematics of Computation 48:329-39.
Singh, S. 1999. The Code Book. London: Fourth Estate.
1. See “The possibility of secure non-secret digital encryption,” available at www.cesg.gov.uk/site/publications/media/possnse.pdf.