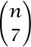The Princeton Companion to Mathematics

VIII.5 Mathematics: An Experimental Science

Herbert S. Wilf

1 The Mathematician’s Telescope

Albert Einstein once said, You can confirm a theory with experiment, but no path leads from experiment to theory.” But that was before computers. In mathematical research now, there’s a very clear path of that kind. It begins with wondering what a particular situation looks like in detail; it continues with some computer experiments to show the structure of that situation for a selection of small values of the parameters of the problem; and then comes the human part: the mathematician gazes at the computer output, attempting to see and to codify some patterns. If this seems fruitful, then the final step requires the mathematician to prove that the apparent pattern is really there, and is not a shimmering mirage above the desert sands.

A computer is used by a pure mathematician in much the same way that a telescope is used by a theoretical astronomer. It shows us “what’s out there.” Neither the computer nor the telescope can provide a theoretical explanation for what it sees, but both of them extend the reach of the mind by providing numerous examples that might otherwise be hidden, and from which one has some chance of perceiving, and then demonstrating, the existence of patterns, or universal laws.

In this article I would like to show you some examples of this process at work. Naturally the focus will be on examples in which some degree of success has been realized, rather than on the much more numerous cases where no pattern could be perceived, at least by my eyes. Since my work is mainly in combinatorics and discrete mathematics, the focus will also be on those areas of mathematics. It should not be inferred that experimental methods are not used in other areas; only that I don’t know those applications well enough to write about them.

In one short article we cannot even begin to do justice to the richly varied, broad, and deep achievements of experimental mathematics. For further reading, see the journal Experimental Mathematics and the books by Borwein and Bailey (2003) and Borwein et al. (2004).

In the following sections we give first a brief description of some of the useful tools in the armament of experimental mathematics, and then some successful examples of the method, if it is a method. The examples have been chosen subject to fairly severe restrictions:

(i) the use of computer exploration was vital to the success of the project; and

(ii) the outcome of the effort was the discovery of a new theorem in pure mathematics.

I must apologize for including several examples from my own work, but those are the ones with which I am most familiar

2 Some of the Tools in the Toolbox

2.1 Computer Algebra Systems

The mathematician who enjoys using computers will find an enormous number of programs and packages available, beginning with the two major computer algebra systems (CASs), Maple and Mathematica. These programs can provide so much assistance to a working mathematician that they must be regarded as essential pieces of one’s professional armamentarium. They are extremely user-friendly and capable.

Typically one uses a CAS in interactive mode, meaning that you type in a one-line command and the program responds with its output, then you type in another line, etc. This modus operandi will suffice for many purposes, but for best results one should learn the programming languages that are embedded in these packages. With a little knowledge of programming, one can ask the computer to look at larger and larger cases until something nice happens, then take the result and use another package to learn something else, and so forth. Many are the times when I have written little programs in Mathematica or Maple and then gone away for the weekend leaving the computer running and searching for interesting phenomena.

2.2 Neil Sloane’s Database of Integer Sequences

Aside from a CAS, another indispensable tool for experimentally inclined mathematicians, particularly for combinatorialists, is Neil Sloane’s “On-Line Encyclopedia of Integer Sequences,” which is on the Web at www.research.att.com/-njas. At present, this contains nearly 100000 integer sequences and has full search capabilities. A great deal of information is given for each sequence.

Suppose that for each positive integer n you have an associated set of objects that you want to count. You might, for example, be trying to determine the number of sets of size n with some given property, or you might wish to know how many prime divisors n has (which is the same as counting the set of these prime divisors). Suppose further that you’ve found the answer for n 1, 2, 3, . . . , 10, say, but you haven’t been able to find any simple formula for the general answer.

Here’s a concrete example. Suppose you’re working on such a problem, and the answers that you get for n = 1,2 . . . , 10 are 1, 1, 1, 1, 2, 3, 6, 11, 23, 47. The next step should be to look online to see if the human race has encountered your sequence before. You might find nothing at all, or you might find that the result that you’d been hoping for has long since been known, or you might find that your sequence is mysteriously the same as another sequence that arose in quite a different context. In the third case, an example of which is described below in section 3, something interesting will surely happen next. If you haven’t tried this before, do look up the little example sequence above, and see what it represents.

2.3 Krattenthaler’s Package “Rate”

A very helpful Mathematica package for guessing the form of hypergeometric sequences has been written by Christian Krattenthaler and is available from his Web site. The name of the package is Rate (rot’-eh), which is the German word for “guess.”

To say what a hypergeometric sequence is, let’s first recall that a rational function of n is a quotient of two polynomials in n, like (3n² + 1)/(n³ + 4). A hypergeometric sequence {t_n}_n≥0 is one in which the ratio t_n+1/t_n is a rational function of the index n. For example, if t_n = 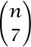then t_n+1/t_n works out to be (n + 1)/ (n - 6), which is a rational function of n, so {t_n}_n≥0 is a hypergeometric sequence. Other examples are all of which are easily seen to be hypergeometric.

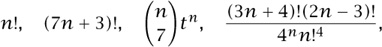
If you input the first several members of the unknown sequence, Rate will look for a hypergeometric sequence that takes those values. It will also look for a hyper-hypergeometric sequence (i.e., one in which the ratio of consecutive terms is hypergeometric), and a hyper-hyper-hypergeometric sequence, etc.

For example, the line

Rate[1,1/4,1/4,9/16,9/4,225/16]

elicits the (somewhat inscrutable) output

{4^1—i0(-1 + ⁱ0)!²}.

Here i0 is the running index of Rate, so we would normally write that answer as, say,

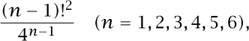
which fits the input sequence perfectly. Rate is a part of the Superseeker front end to the Integer Sequences database, discussed in section 2.2 above.

2.4 Identification of Numbers

Suppose that, in the course of your work, you encountered a number, let’s call it β, which, as nearly as you could calculate it, was 1.218041583332573. It might be that β is related to other famous mathematical constants, like π, e, , and so forth, or it might not. But you’d like to know.

The general problem that is posed here is the following. We are given k numbers, α₁, . . . , αk (the basis), and a target number α. We want to find integers m, m_l, . . . , m_k such that the linear combination is an extremely close numerical approximation to 0.

If we had a computer program that could find such integers, how would we use it to identify the mystery constant β = 1.218041583332573? We would take the α_i to be a list of the logarithms of various well-known universal constants and prime numbers, and we would take α = log β. For example, we might use

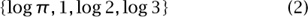
as our basis. If we then find integers m, m₁, . . . , m₄ such that

is extremely close to 0, then we will have found that our mystery number β is extremely close to

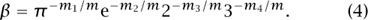
At this point we will have a judgment to make. If the integers m_i seem rather large, then the presumed evaluation (4) is suspect. Indeed, for any target α and basis {α_i} we can always find huge integers {m_i} such that the linear combination (1) is exactly 0, to the limits of machine precision. The real trick is to find a linear combination that is extraordinarily close to 0, while using only “small” integers m, m_i, and that is a matter of judgment. If the judgment is that the relation found is real, rather than spurious, then there remains the little job of proving that the suspected evaluation of α is correct, but that task is beyond our scope here. For a nice survey of this subject, see Bailey and Plouffe (1997).

There are two major tools that can be used to discover linear dependencies such as (1) among the members of a set of real numbers. They are the algorithms PSLQ of Ferguson and Forcade (1979), and LLL, of Lenstra et al. (1982), which uses their lattice basis reduction algorithm. For the working mathematician, the good news is that these tools are available in CASs. For example, Maple has a package, IntegerRelations [LinearDependency], which places the PSLQ and the LLL algorithms at the immediate disposal of the user. Similarly there are Mathematica packages on the Web that can be freely downloaded and which perform the same functions.

An application of these methods will be given in section 7. For a quick illustration, though, let us try to recognize the mystery number β = 1.218041583332573. We use as a basis the list in (2) above, and we put this list, augmented by log 1.218041583332573, into Maple’s IntegerRelations[LinearDependency] package. The output is the integer vector [2, -6, 0, 3, 4], which tells us that β = π³/36, to the number of decimal places carried.

2.5 Solving Partial Differential Equations

I had occasion recently to need the solution to a certain partial differential equation (PDE) that arose in connection with a research problem that was posed by Graham et al. (1989). It was a first-order linear PDE, so in principle the METHOD OF CHARACTERISTICS [III.49 §2.1] gives the solution. As those who have tried that method know, it can be fraught with technical difficulties relating to the solution of the associated ordinary differential equations.

However, some extremely intelligent packages are available for solving PDEs. I used the Maple command pdsolve to handle the equation

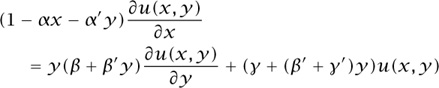
with u(0, y) = 1. pdsolve found that

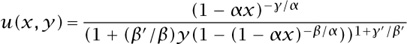
is the solution, and that enabled me to find explicit formulas for certain combinatorial quantities, with much less work and fewer errors than would otherwise have been possible.

3 Thinking Rationally

The following problem appeared in the September/October 1997 issue of Quantum (and was chosen by Stan Wagon for the Problem of the Week archive).

How many ways can 90 316 be written as

a + 2b + 4c + 8d + 16e + 32f + . . . ,

where the coefficients can be any of 0, 1, or 2?

In standard combinatorial terminology, the question asks for the number of partitions of the integer 90316 into powers of 2, where the multiplicity of each part is at most 2.

Let’s define b(n) to be the number of partitions of n, subject to the same restrictions. Thus b(5) = 2 and the two relevant partitions are 5 = 4 + 1 and 5 = 2 + 2 + 1. Then it is easy to see that b(n) satisfies the recurrences b(2n+ 1) = b(n) and b(2n+ 2) = b(n) + b(n + 1), for n = 0, 1, 2 . . . ,with b(0) = 1.

It is now easy to calculate particular values of b(n). This can be done directly from the recurrence, which is quite fast for computational purposes. Alternatively, it can be shown quite easily that our sequence {b(n)}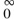 has the generating function

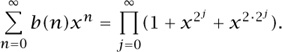
(Generating functions are discussed in ALGEBRAIC AND ENUMERATIVE COMBINATORICS [IV.18 §§2.4, 3], Or see Wilf (1994).) This helps us to avoid much programming when working with the sequence, because we can use the built-in series-expansion instructions in Mathematica or Maple to show us a large number of terms in this series quite rapidly. Returning to the original question from Quantum, it is a simple matter to compute b (90316) = 843 from the recurrence. But let’s try to learn more about the sequence {b(n)} in general. To do that we open up our telescope, and calculate the first ninety-five members of the sequence, i.e., {b(n)}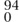, which are shown in table 1. The question is now, as it always is in the mathematics laboratory, what patterns do you see in these numbers?

Just as an example, one might notice that when n is 1 less than a power of 2, it seems that b(n) = 1. The reader who is fond of such puzzles is invited to cease reading here for the moment (without peeking at the next paragraph), and look at table 1 to spend some time finding whatever interesting patterns seem to be there. Computations up to n = 94 aren’t as helpful for a quest like this as computations up to n = 1000 or so might be, so the reader is also invited to compute a much longer table of values of b(n), using the above recurrence formulas, and to study it carefully for fruitful patterns.

OK, did you notice that if n = 2^a then b(n) appears to be a + 1? How about this one: in the block of values of n between 2^a and 2^{a + 1} – 1, inclusive, the largest value of b (n) that seems to occur is the Fibonacci number F_a+2. There are many intriguing things going on in this sequence, but the one that was of crucial importance in understanding it was the observation that consecutive values of b(n) seem always to be relatively prime.1

It was totally unexpected to find a property of the values of this sequence that involved the multiplicative structure of the positive integers, rather than their additive structure, which would have been quite natural. This is because the theory of partitions of integers belongs to the additive theory of numbers, and multiplicative properties of partitions are rare and always cherished.

Once this relative primality is noticed, the proof is easy. If m is the smallest n for which b(n), b(n + 1) fail to be relatively prime, then suppose p > 1 divides both of them. If m = 2k + 1 is odd, then the recurrence

Table 1 The first ninety-five values of b(n).

implies that p divides b(k) and b(k + 1), contradicting the minimality, whereas if m = 2k is even, the recurrence again gives that result, finishing the proof.

Why was it so interesting that consecutive values appeared to be relatively prime? Well, at once that raised the question of whether every possible relatively prime pair (r, s) of positive integers occurs as a pair of consecutive values of this sequence, and if so, whether every such pair occurs once and only once. Both of those possibilities are supported by the table of values above, and upon further investigation both turned out to be true. See Calkin and Wilf (2000) for details.

The bottom line here is that every positive rational number occurs once and only once, and in reduced form, among the members of the sequence {b(n)/b(n + 1)}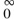. Hence the partition function b(n) induces an enumeration of the rational numbers, a result which was found by gazing at a computer screen and looking for patterns.

Moral: be sure to spend many hours each day gazing at your computer screen and looking for patterns.

4 An Unexpected Factorization

One of the great strengths of computer algebra systems is that they are very good at factoring. They can factor very large integers and very complicated expressions. Whenever you run into some large expression as the answer to a problem that interests you, it is good practice to ask your CAS to factor it for you. Sometimes the results will surprise you. This is one such story.

The theory of Young tableaux forms an important part of modern combinatorics. To create a Young tableau we choose a positive integer n and a partition n = a₁ + a₂ + . . . + a_k of that integer. We’ll use the integer n = 6 and the partition 6 = 3 + 2 + 1 as an example. Next we draw the Ferrers board of the partition, which is a truncated chessboard that has a₁ squares in its first row, a₂ in its second row, etc., the rows being left-justified. In our example, the Ferrers board is as shown in figure 1.

To make a tableau, we insert the labels 1, 2, . . . , n into the n cells of the board in such a way that the labels increase from left to right across each row and increase from top to bottom down every column. With our example, one way to do this is as shown in figure 2.

One of several important properties of tableaux is that there is a one-to-one correspondence, known as the Robinson-Schensted-Knuth (RSK) correspondence, which assigns to every permutation of n letters a pair of tableaux of the same shape. One use of the RSK correspondence is to find the length of the longest increasing subsequence in the vector of values of a given permutation. It turns out that this length is the same as the length of the first row of either of the tableaux to which the permutation corresponds under the RSK

Figure 1 The Ferrers board.

Figure 2 A Young tableau.

mapping. This fact gives us a good way, algorithmically speaking, of finding the length of the longest increasing subsequence of a given permutation.

Now suppose that u_k(n) is the number of permutations of n letters that have no increasing subsequence of length greater than k. A spectacular theorem of Gessel (1990) states that

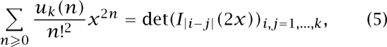
in which I_v(t) is (the modified Bessel function)

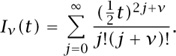
At any rate, it seems fairly “spectacular” to me that when you place various infinite series such as the above into a k × k determinant and then expand the determinant, you should find that the coefficient of x²ⁿ, when multiplied by n!², is exactly the number of permutations of n letters with no increasing subsequence longer than k.

Let’s evaluate one of these determinants, say the one with k = 2. We find that

which of course factors as (I₀ + I₁)(I₀ - I₁). The arguments of the I_v are all 2x and have been omitted.

When k = 3, no such factorization occurs. If you ask your CAS for this determinant when k = 4, it will show you

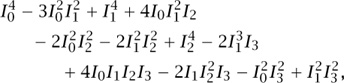
where now we have abbreviated I_v (2x) simply by I_v. If we ask our CAS to factor this last expression, it (surprisingly) replies with

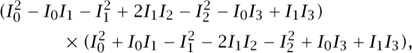
which is actually of the form (A + B) (A - B), as a quick inspection will reveal.

We have now observed, experimentally, that for k = 2 and k = 4 Gessel’s k × k determinant has a nontrivial factorization of the form (A + B) (A - B), in which A and B are certain polynomials of degree k/2 in the Bessel functions. Such a factorization of a large expression in terms of formal Bessel functions simply cannot be ignored. It demands explanation. Does this factorization extend to all even values of k? It does. Can we say anything in general about what the factors mean? We can.

The key point, as it turns out, is that in Gessel’s determinant (5), the matrix entries depend only on |i — j| (such a matrix is called a Toeplitz matrix). The determinants of such matrices have a natural factorization, as follows. If a₀, a₁, . . . is some sequence, and a_-i = a_i then we have

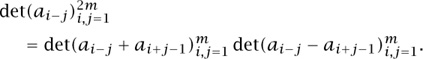
When we apply this fact to the present situation it correctly reproduces the above factorizations for k = 2, 4, and generalizes them to all even k, as follows.

Let y_k (n) be the number of Young tableaux of n cells whose first row is of length at most k, and let

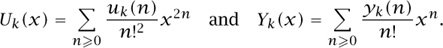
In terms of these two generating functions, the general factorization theorem states that

U_k(x) = Y_k(x)Y_k(—x) (k = 2,4,6,. . .).

Why is it useful to have such factorizations? For one thing we can equate the coefficients of like powers of x on both sides of this factorization (try it!). We then find an interesting explicit formula that relates the number of Young tableaux of n cells whose first row is of length at most k, on the one hand, and the number of permutations of n letters that have no increasing subsequence of length greater than k, on the other. No more direct proof of this relationship is known. For more details and some further consequences, see Wilf (1992).

Moral: cherchez les factorisations!

5 A Score for Sloane’s Database

Here is a case study in which, as it happens, not only was Sloane’s database utilized, but Sloane himself was one of the authors of the ensuing research paper.

Eric Weisstein, the creator of the invaluable Web resource MathWorld, became interested in the enumeration of 0-1 matrices whose eigenvalues are all positive real numbers. If f (n) is the number of n × n matrices whose entries are all 0s and 1s and whose eigenvalues are all real and positive, then by computation, Weisstein found for f (n) the values

1, 3, 25, 543, 29 281 (for n = 1, 2, . . . , 5).

Upon looking up this sequence in Sloane’s database, Weisstein found, interestingly, that this sequence is identical, as far as it goes, with sequence A003024 in the database. The latter sequence counts vertex-labeled acyclic directed graphs (“digraphs”) of n vertices, and so Weisstein’s conjecture was born:

[T]he number of vertex-labeled acyclic digraphs of n vertices is equal to the number of n × n 0-1 matrices whose eigenvalues are all real and positive.

This conjecture was proved in McKay et al. (2003). En route to the proof of the result, the following somewhat surprising fact was shown.

Theorem 1. If a 0-1 matrix A has only real positive eigenvalues, then those eigenvalues are all equal to 1.

To prove this, let {λ_i} be the eigenvalues of A. Then

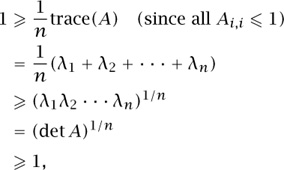
in which the third line uses the arithmetic-geometric mean inequality, and the last line uses the fact that det A is a positive integer. Since the arithmetic and geometric means of the eigenvalues are equal, the eigenvalues are all equal, and in fact all λ_i(A) = 1.

The proof of the conjecture itself works by finding an explicit bijection between the two sets that are being counted. Indeed, let A be an n × n matrix of 0s and 1s with positive eigenvalues only. Then those eigenvalues are all 1s, so the diagonal of A is all 1s, whence the matrix A - I also has solely 0s and 1s as its entries. Regard A - I as the vertex adjacency matrix of a digraph G. Then (it turns out that) G is acyclic.

Conversely, if G is such a digraph, let B be its vertex adjacency matrix. By renumbering the vertices of G, if necessary, B can be brought to triangular form with zero diagonal. Then A = I + B is a 0-1 matrix with positive real eigenvalues only. But then the same must have been true for the matrix I + B before simultaneously renumbering its rows and columns. For more details and more corollaries, see McKay et al. (2003).

Moral: see if you can find your sequence in the online encyclopedia!

6 The Twenty-One-Stage Rocket

Now we’ll describe a successful attack that was carried out by Andrews (1998) on the problem of evaluating the Mills-Robbins-Rumsey determinant, which is the determinant of the n × n matrix

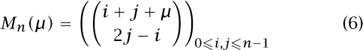
This problem arose (Mills et al. 1987) in connection with the study of plane partitions. A plane partition of an integer n is an (infinite) array n_i,j of nonnegative integers whose sum is n, subject to the restriction that the entries n_i,j are nonincreasing across each row, and also down each column.

It turns out that det M_n(μ) can be expressed neatly as a product, namely as

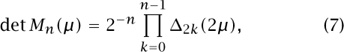
in which

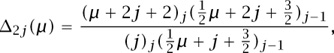
and (x)_j is the rising factorial x (x + 1) . . . (x + j - 1).

The strategy of Andrews’s proof is elegant in conception and difficult in execution: we are going to find an upper triangular matrix E_n (μ), whose diagonal entries are all 1s, such that the matrix

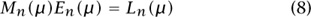
is lower triangular, with the numbers {Δ_2j (2μ)}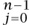 on its diagonal. Of course, if we can do this, then from (8), since det E_n (μ) = 1, we will have proved the theorem (7), since the determinant of the product of two matrices is the product of their determinants, and the determinant of a triangular matrix (i.e., of a matrix all of whose entries below the diagonal are 0s) is simply the product of its diagonal entries.

But how shall we find this matrix E_n (μ)? By holding tightly to the hand of our computer and letting it guide us there. More precisely,

(i) we will look at the matrix E_n (μ) for various small values of n, and from those data we will conjecture the formula for the general (i, j) entry of the matrix; and then

(ii) we will (well actually “we” won’t, but Andrews did) prove that the conjectured entries of the matrix are correct.

It was in step (ii) above that an extraordinary twentyone-stage event occurred which was successfully managed by Andrews. What he did was to set up a system of twenty-one propositions, each of them a fairly technical hypergeometric identity. Next, he carried out a simultaneous induction on these twenty-one propositions. That is to say, he showed that if, say, the thirteenth proposition was true for a certain value of n, then so was the fourteenth, etc., and if they were all true for that value of n, then the first proposition was true for n + 1. The reader should be sure to look at Andrews (1998) to gain more of the flavor and substance of what was done than can be conveyed in this short summary.

Here we will confine ourselves to a few comments about step (i) of the program above. So, let’s look at the matrix E_n (μ) for some small values of n. The condition that E_n (μ) is upper triangular with 1s on the diagonal means that

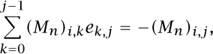
for 0 ≤ i ≤ j - 1 and 1 ≤ j ≤ n - 1. We can regard these as 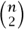equations in the 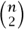above-diagonal entries of E_n (μ) and we can ask our CAS to find those entries, for some small values of n. Here is E₄ (μ):

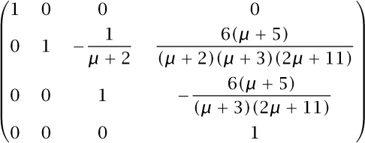
At this point the news is all good. While it is true that the matrix entries are fairly complicated, the fact that leaps off the page and warms the heart of the experimental mathematician is that all of the polynomials in μ factor into linear factors with pleasant-looking integer coefficients. So there is hope for conjecturing a general form of the E matrix. Will this benign situation persist when n = 5? A further computation reveals that E₅ (μ) is as shown in figure 3. Now it is a “certainty” that some nice formulas exist for the entries of the general matrix E_n (μ). The Rate package, described in section 2.3, would certainly facilitate the next step, which is to find general formulas for the entries of the E matrix. The final result is that the (i, j) entry of E_n (μ) is 0 if i > j and

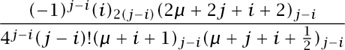
otherwise.

After divining that the E matrix has the above form, Andrews now faced the task of proving that it works, i.e., that M_nE_n (μ) is lower triangular and has the diagonal entries specified above. It was in this part of the work that the twenty-one-fold induction was unleashed. Another proof of the evaluation of the Mills-Robbins-Rumsey determinant is in Petkovšek and Wilf (1996). That proof begins with Andrews’s discovery of the above form of the E_n (μ) matrix, and then uses the machinery of the so-called WZ method (Petkovšek et al. 1996), instead of a twenty-one-stage induction, to prove that the matrix performs the desired triangulation (8).

Moral: never give up, even when defeat seems certain.

7 The Computation of π

In 1997, a remarkable formula for π was found (Bailey et al. 1997). This formula permits the computation of just a single hexadecimal digit of π, if desired, using minimal space and time. For example, we might compute the trillionth digit of π, without ever having to deal with any of the earlier ones, in a time that is faster than what we might attain if we had to calculate all of the first trillion digits. For example, Bailey et al. found that in the hexadecimal expansion of π the block of fourteen digits in positions 10¹⁰ through 10¹⁰ + 13 are 921C73C6838FB2. The formula is

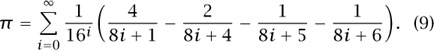
Figure 3 The upper triangular matrix E₅ (μ).

In our discussion here we will limit ourselves to describing how we might have found the specific expansion (9) once we had decided that an interesting expansion of the form

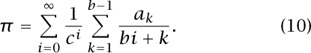
might exist. This, of course, leaves open the question of how the discovery of the form (10) was singled out in the first place.

The strategy will be to use the linear dependency algorithm described in section 2.4. More precisely, we want to find a nontrivial integer linear combination of π and the seven numbers

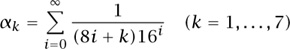
that sums to 0. As in equation (3), we now compute the seven numbers α_j and we look for a relation

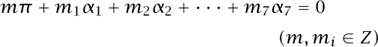
by using, for example, the Maple IntegerRelations package. The output vector,

(m, m1, m2, . . . , m7) = (1, —4, 0, 0, 2, 1, 1, 0),

yields the identity (9). You should do this calculation for yourself, then prove that the apparent identity is in fact true, and, finally, look for something similar that uses powers of 64 instead of 16. Good luck!

Moral: even as late as the year 1997 C.E., something new and interesting was said about the number π.

8 Conclusions

When computers first appeared in mathematicians’ environments the almost universal reaction was that they would never be useful for proving theorems since a computer can never investigate infinitely many cases, no matter how fast it is. But computers are useful for proving theorems despite that handicap. We have seen several examples of how a mathematician can act in concert with a computer to explore a world within mathematics. From such explorations there can grow understanding, and conjectures, and roads to proofs, and phenomena that would not have been imaginable in the pre-computer era. This role of computation within pure mathematics seems destined only to expand over the coming years and to be imbued into our students along with EUCLID’s [VI.2] axioms and other staples of mathematical education.

At the other end of the rainbow there may lie a more far-reaching role for computers. Perhaps one day we will be able to input some hypotheses and a desired conclusion, press the “Enter” key, and get a printout of a proof. There are a few fields of mathematics in which we can do such things, notably in the proofs of identities (Petkovšek et al. 1996; Greene and Wilf 2007), but in general the road to that brave new world remains long and uncharted.