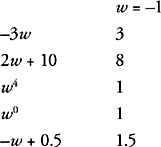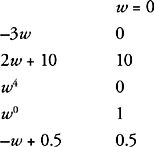ANSWERS
Drill 1
Drill 2
Drill 3
Drill 4
EXPLANATIONS
Drill 1
1. B Plug in a value that meets the given requirements; try x = 15. The remainder when 15 is divided by 10 is 5; Quantity B is greater, so eliminate choices (A) and (C). Any acceptable value of x gives the same outcome, so select choice (B).
2. E Find the value of each fraction by multiplying the numbers in the numerator and adding the numbers in the denominator. The value of each fraction is 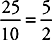 . Add the two fractions:
. Add the two fractions: 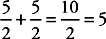 .
.
3. D Solve for m. If |1 – 5| = |5 – m|, then |– 4| = |5 – m|, or 4 = |5 – m|. When you see absolute values, remember to consider both positive and negative solutions: 5 − m = 4 or 5 − m = −4, so
m can equal 1 or 9, leaving you with choice (D) for the answer.
4. D Try Plugging In; one set of values that could work is x = −2, y = 0, and z = 2. In this case, both Quantity A and Quantity B have a value of 0. Eliminate choices (A) and (B). However, another set of values that could work is x = −6, y = −4,
and z = −2. With this set of values, Quantity A has a value of 24 and Quantity B has a value of 8. Eliminate choice (C). You are left with choice (D) for the answer.
5. D This problem offers a good opportunity to plug in the answers—for simplicity’s sake, start with the integers. If c = 6, choice (B), then 3b + 2(6) = 18, so 3b + 12 = 18, 3b = 6, and b = 2. The only other requirement given is that bc
≠ 0, so 6 is, in fact, a possible value of c. If c = 9, as in choice (D), then 3b + 2(9) = 18, so 3b + 18 = 18, 3b = 0, and b = 0. A value of 0 for b would violate the given requirement, so 9 is NOT a possible value of c.
6. C 30 apples at 40 cents apiece cost $12. Buying 30 apples at 3 per dollar would cost $10. Therefore, the sale price is $2 less than the normal price.
7. A When y = −1, Quantity A is −2 and Quantity B is −20. Eliminate choices (B) and (C). Plug in another value for y. When y = −100, Quantity A is −200 and Quantity B is −2,000. Quantity A is always greater.
8. B The two positive integers must have a product of 28, so find the factor pairs of 28: 1 and 28, 2 and 14, and 4 and 7. Only choice (B) gives a possible difference: 7 − 4 = 3.
9. B Solve this problem by brute force, but be systematic about it. Set Y has a finite number of elements, so list them out and start finding the products when those elements are multiplied by positive multiples of 5. Set Y = {3, 5, 7, 11, 13, 17, 19}, so multiplying by
5—the first positive multiple of 5—yields 15, 25, 35, 55, 65, 85, and 95; that’s 7 elements for set Z thus far. Multiplying by 10—the next positive integer multiple of 5—yields 3 more products, 30, 50, and 70. Multiplying by 15 yields two new products, 45 and 75; multiplying by 20 yields only one new product, 60. That’s a total of 13 elements for set Z so far. You already have 75 as a member of set Z, so
multiplying by 25 yields no new products; multiplying by 30 yields the final new product, 90. Set Z thus consists of 14 elements: set Z = {15, 25, 30, 35, 45, 50, 55, 60, 65, 70, 75, 85, 90, 95}. If you got choice (E), you may have mistakenly included 2 as an element of set Y.
10. B Plug in values for the variables, such as u = 2, v = 4, x = 6, y = 8, and z = 10. With these values, the expression equals  . Try halving each of the values to find which one would change the
value of the expression to
. Try halving each of the values to find which one would change the
value of the expression to  . Halving v to 2 works; the answer is choice (B).
. Halving v to 2 works; the answer is choice (B).
11. D Time to Plug In! If you make m = 2 and n = 3, then Quantity A becomes 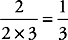 , and Quantity B becomes
, and Quantity B becomes 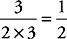 . Quantity B is bigger; eliminate choices (A) and
(C). However, if you make and n = 2, then the situation is reversed: Quantity A will be
. Quantity B is bigger; eliminate choices (A) and
(C). However, if you make and n = 2, then the situation is reversed: Quantity A will be  , and Quantity B will be
, and Quantity B will be  . Eliminate choice (B); the answer must be choice (D).
. Eliminate choice (B); the answer must be choice (D).
12. D Try rounding your values before you calculate. The expression can be estimated as 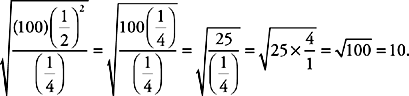
13. B The prime numbers less than 10 are 2, 3, 5, and 7—don’t forget, 1 is not prime. Their sum is 17, and 3 × 17 = 51. The only prime numbers between 20 and 30 are 23 and 29, and their sum is 52. Quantity B is greater.
14. C It is easier to work with the factors of Tasha’s favorite number, rather than with the number itself. Write out the number as 3 × 3 × 17 × 17 and make a list of the divisors—or factors—in pairs. The pairs are: 1 and 3 × 3 × 17 × 17, 3 and 3 × 17
× 17, 17 and 3 × 3 × 17, 3 × 3 and 17 × 17, and 3 × 17 and 3 × 17. The final pair contains only one distinct factor, giving you a total of 9 factors.
Drill 2
1. D Try Plugging In on this one. If x = 4, then choice (A) is  or 0.25, choice (B) is
or 0.25, choice (B) is  or 0.2, choice (C) is
or 0.2, choice (C) is  or 0.8, choice (D) is
or 0.8, choice (D) is 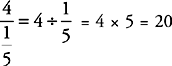 , and choice (E) is
, and choice (E) is 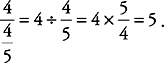 Choice (D) is the greatest.
Choice (D) is the greatest.
2. C Rather than listing out all of the prime numbers up to 43, stay focused on the unique number, 2, the only even prime number. All of the choices are odd, and two odd numbers would yield an even sum, so you’ll only be able to eliminate answers by adding 2 to an odd number. Each of the incorrect
answers, therefore, is the sum of 2 and the previous prime number: Choice (A) is 2 + 5; choice (B) is 2 + 17; choice (D) is 2 + 29; and choice (E) is 2 + 41. The answer is choice (C).
3. E Plug in a value for r: The first integer multiple of 8 is 8 itself. Only choice (E) fails to yield an integer: 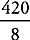 = 52.5.
= 52.5.
4. 12 Ballpark that 960 is about 1,000, which is 10 × 10 × 10. Then test a set of consecutive even integers near 10, such as 10 × 12 × 14 = 1,680. This product is too large. Try 8 × 10 × 12 = 960, giving you z = 12.
5. D Eliminate choices (A) and (E) because they are not divisible by 12. Eliminate choices (B) and (C) because they are not divisible by 17.
6. D The intervals between consecutive prime numbers does not follow a consistent, predictable pattern. Prove it by Plugging In: Try f = 2, g = 3, and h = 5. Now f + g + h = 10 and 3g = 9. Quantity A is greater; eliminate choices (B) and (C). Now try
f = 7, g = 11, and h = 13. This time, f + g + h = 31, and 3g = 33. Quantity B is now greater. Eliminate choice (A), and you’re left with choice (D).
7. D The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96. Eight of these numbers are less than 20.
8. A and C
As soon as you see variables in the answer choices, set up your scratch paper to Plug In. Start with easy numbers like p = 3 and q = 5, and eliminate any answer choice that doesn’t yield an odd result. Choice (A) is 15, so keep it. Choice
(B) is 30, so eliminate choice (B). Choice (C) is 45, so keep it. Choice (D) is 258, and Choice (E) is 368, so you can eliminate both; if you recognize them as the sum of two odd numbers, you don’t have to calculate either of them. It’s a must be problem, so try another set of numbers in choices (A) and (C) to be sure; as long as p and q are both positive odd integers, choices (A) and (C) will always work.
9. C If a and b are integers with a product of −5, then there are only 4 options: a = 5 and b = −1; a = −5 and b = 1; a = 1 and b = −5; and a = −1 and b = 5. The requirement that
a − b > 0 eliminates the second and fourth options, leaving only a = 5 and b = −1 and a = 1 and b = −5. (I) and (II) are both true for these two cases and (III) is not true if a = 1, making choice (C) the answer.
10. C The first equation tells you that y cannot be a negative number. The second equation tells you that y cannot be a positive number. Therefore, y must be 0.
11. D Plug in values for x and y that fit the figure: Try x =  and
and  . Now, plug these numbers into each of the choices and use POE. Only
choice (D) is correct:
. Now, plug these numbers into each of the choices and use POE. Only
choice (D) is correct: 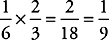 , which is less than
, which is less than  .
.
12. C If the remainder is 3, then 5n must be 3 more than a multiple of 4, such as 4, 8, 12, or 16. Try adding 3 to these multiples to find a possible value for 5n. 12 + 3 yields 15 as a value for 5n; n = 3. Quantity A is the remainder when 30 is divided by 4, or 2. Eliminate choices (A) and
(B). Try a different number. If n is 7, then 5n is 35, which also has a remainder of 3 when divided by 4. In Quantity A, 70 divided by 4 has a remainder of 2. For any other numbers you try, choice (C) will be the answer.
13. D Plug in values for a and b. If a = −2 and b = 2, then Quantity B is greater. Eliminate choices (A) and (C). If  and b =
and b =  , then Quantity A is greater. Eliminate choice (B).
, then Quantity A is greater. Eliminate choice (B).
Drill 3
1. E Plug in 12 for the number of people in the office, because the remainder is 0 when 12 is divided by 12. Because 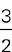 × 12 is 18, and the remainder when 18 is divided by 12 is 6, choice (E) must be correct.
× 12 is 18, and the remainder when 18 is divided by 12 is 6, choice (E) must be correct.
2. A Try Plugging In. If a = 15, b = 30, and c = 60, Quantity A is 30 because c cannot divide into b even one time. Quantity B is 0 because 90 divided by 15 has no remainder. Eliminate choices (B) and (C). Try a new set of numbers to further narrow your choices. If
a = 30, b = 45, and c = 120, Quantity A is 45, and Quantity B is 15. The answer is choice (A).
3. D, E, and F
It’s an algebra question with numbers for answer choices, so set up your scratch paper to plug in the answers. Start with choice (C): If Emma is 17, then Merrick is 14, and Aliza is 22. That’s too young, so eliminate choices (A), (B), and (C).
Now try choice (D): If Emma is 20, then Merrick is 17, and Aliza is 25. That’s old enough, so select choices (D), (E), and (F).
4. E Estimate that D is approximately 2.8 and A is approximately 0.8. So the answer is 2.8 ÷ 0.8, or 3.5, which is closest to choice (E).
5. 41 Half of the integers from 1 to 100—inclusive—are even, so set X has 50 members. Set Y has 19 members, the integers divisible by 5 from 1 to 100 exclusive, so don’t include 100. Of the 19 members of set Y, 9 are even and therefore, in set X. The 50
members of set X minus the 9 members that are also in set
Y yields 50 − 9 = 41 members.
6. C To solve this problem, Plug In for a and b, but don’t forget your restrictions. If a = −4, then a value of – for b would yield a product greater
than 0 but less than |a|. Only choice (C) works.
for b would yield a product greater
than 0 but less than |a|. Only choice (C) works.
7. C The only number that is positive, even, and prime is 2. Because the number is divisible by 2, it must be even.
8. E First, list all of the factors of 210. The easiest way to do this is in pairs, starting with 1 and 210 (remember, the number itself is considered one of its factors). Count up from one and check to see if each number you count is a factor of 210.
2 and 105
3 and 70
5 and 42
7 and 3
10 and 21
14 and 15
9. 3 Adding the numbers together won’t take long, but there is a shortcut to this problem. Match up the smallest number of miles (1) with the largest number of miles (12), and then the second smallest (2) with the second largest (11), etc. until all the numbers are matched up.
2 11
3 10
4 9
5 8
6 7
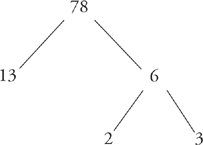
10. D Start by translating her earnings on her shares of Capital Growth Fund were three times half of her earnings on her investment in Venture Index Fund from English to math. Represent her earnings in Capital Growth Fund as C. Were translates to “ = .”
Three times half is “3 ×  ,” and of is “×” (multiplication). Represent Melania’s earnings from Venture Index Fund as V, and the resulting equation is C =
,” and of is “×” (multiplication). Represent Melania’s earnings from Venture Index Fund as V, and the resulting equation is C = 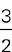 V. Total earnings on the two funds were $1,250, so
C + V = $1,250, and since C =
V. Total earnings on the two funds were $1,250, so
C + V = $1,250, and since C = 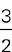 V, that equation can be rewritten as
V, that equation can be rewritten as 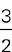 V + V = $1,250, or
V + V = $1,250, or  V = $1,250. Solve this to find that V = $500 earned on Venture Index Fund.
Notice that this is a partial answer that is included among the answer choices. Continuing to solve, represent the amount of money invested in Venture Index Fund as x. Melania had three times as much money invested in Capital Growth Fund as in Venture Index Fund; therefore she had 3x dollars invested in Capital Growth Fund. She had a total of $20,000 invested in the two funds; therefore 3x + x = $20,000. Solve to find that x =
$5,000 invested in Venture Index Fund. Now, plug in those numbers to the percent interest formula given in the problem,
V = $1,250. Solve this to find that V = $500 earned on Venture Index Fund.
Notice that this is a partial answer that is included among the answer choices. Continuing to solve, represent the amount of money invested in Venture Index Fund as x. Melania had three times as much money invested in Capital Growth Fund as in Venture Index Fund; therefore she had 3x dollars invested in Capital Growth Fund. She had a total of $20,000 invested in the two funds; therefore 3x + x = $20,000. Solve to find that x =
$5,000 invested in Venture Index Fund. Now, plug in those numbers to the percent interest formula given in the problem, 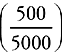 ×100, which equals the credited answer, choice (D), 10. You will arrive at the remaining, wrong answer choices if you mistakenly solve for the percent interest earned on Capital Growth Fund, and/or you represent your answer as a multiplier, rather than a percent (i.e., 0.01
versus 10%).
×100, which equals the credited answer, choice (D), 10. You will arrive at the remaining, wrong answer choices if you mistakenly solve for the percent interest earned on Capital Growth Fund, and/or you represent your answer as a multiplier, rather than a percent (i.e., 0.01
versus 10%).
11. A Let’s translate this question, one step at a time.
12. A, B, and E
To solve this question, turn large numbers into small numbers by working with factors. The prime factors of 154 are 2, 7, and 11; the prime factors of 264 are 2, 2, 2, 3, and 11; and the prime factors of 250 are 2, 5, 5, and 5. The only numbers that must
be a factor of m are those made up of factors contained in the other three numbers. You can’t recount factors that overlap in the different numbers, so you know that m is made up of, at least, three 2’s, one 3, three 5’s, one 7, and one 11. Now check the answers. The prime factors of 176 are 2, 2, 2, 2, and 11, which is one 2 too many, so choice (A) is not a factor; since the question asks you to identify which choices are not
factors, choice (A) is part of the credited response. The prime factors of 242 are 2, 11, and 11, which is one 11 too many, so (B) is also not a factor. The prime factors of 275 are 5, 5, and 11, so choice (C) is a factor. The prime factors of 924 are 2, 2, 3, 7, and 11, so choice (D) is a factor. The prime factors of 2,500 are 2, 2, 5, 5, 5, and 5, which is one 5 too many, so choice (E) is not a factor. And, finally, the prime factors of 7,000 are 2, 2, 2, 5, 5, 5, and 7, so
choice (F) is a factor. The correct answers are choices (A), (B), and (E).
13. B As soon as you see variables in the answer choices, set up your scratch paper to Plug In. If x = 16 and z = 5, then 16 ÷ 5 = 3 remainder 1, so y = 3 and q = 1. Plug your values into the answer choices, and only choice (B) works: 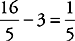 .
.
Drill 4
1. B To solve this question, find the prime factors: The prime factors of 154 are 2, 7, and 11, and the prime factors of 56 are 2, 2, 2, and 7. Thus, the product of 154 and 56 will have the prime factors 2, 2, 2, 2, 7, 7, and 11, or (24)(72)(111). Line up your bases and exponents with the inequalities, and you get a = 4, b = 2, and c = 1 for the bases, and x = 2, y = 7, z = 11 for the exponents. Now axbycz = (42)(27)(111), which equals 16 × 128 × 1, or 2,048. The correct answer is choice
(B).
2. B You can Plug In or solve on this problem. To Plug In, choose a value that fits one of the answer choices, such as x = 2, which would fit in the range for choice (C). If x = 2, then |–3x + 1| = 5, which is true, so we can eliminate any answer choice that doesn’t
include x = 2: choices (A), (D), and (E). Logically, it doesn’t make sense that an inequality with a < sign would have a ≤ sign when it’s been solved, but to be sure, check x = −2. In that case, |–3x + 1| = 7, and is not < 7, so the answer must be choice (B). If you solve this problem, remember that you have to solve both −3x + 1 < 7, and −3x + 1 > 7. Also
remember that you must flip the sign any time you multiply or divide both sides of an inequality by a negative number.
3. 480 Make lists of the multiples for each number. Work on 240 first, then list the multiples of 160 until you find one on the list for 240.

4. 4 To solve this question, write it out. Since there are fewer numbers that yield a remainder of 2 when divided by 7, start there. The first such number is 2, and thereafter they increase by 7; the rest of the list is thus 9, 16, 23, 30, 37, 44, 51, 58, 65, 72, 79, 86, and 93. Rather than list out all the
numbers that yield a remainder of 1 when divided by 3, just select the numbers that meet the requirement from the list you already have: Only 16, 37, 58, and 79 do, so there are 4 values for x.
5. D Plug in values for j and k. Since every number is a multiple of itself, go ahead and start with j = 12 and k = 21; jk is now 252. You can use your on-screen calculator to determine that, of the answer choices, only 28 divides evenly into 252. Choice (D) is
correct.
6. 14 Don’t forget that you can use your on-screen calculator. There’s only one positive integer with no prime factors, the number 1. Therefore, y = 1, and xz = 420. Create a prime factor tree to get the prime factors of 420: 2,
2, 3, 5, and 7. Pick 3 distinct values from that list, such as 2, 3, and 5, and multiply them to find one possible value of x. One example is 2 × 3 × 5 = 30, or one possible value for x. If 30z = 420, then z = 14. Confirm that 14 is not prime, then enter it in the field.
7. D and E
Remember to Plug In multiple times for must be questions. First, use an easy number, such as −1, and try it in each choice:
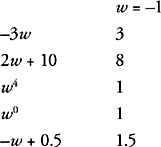
All of the answers are positive, so don’t eliminate anything. Can we eliminate anything by making w smaller? A number such as −10 will allow us to eliminate choice (B), but everything else is still positive. But can w = 0? Non-positive just means the number can’t be positive—it doesn’t mean it can’t be zero.
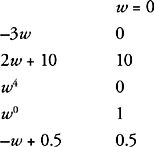
8. D You should Plug In on this question. Variables a and b can be consecutive numbers such as 6 and 12. Plug in consecutive multiples of 8 for x and y, such as 8 and 16. Finding the ratio of the averages is easy now; the averages of each pair of numbers will be the
halfway point between the two numbers. For 6 and 12, the average is 9. For 8 and 16, the average is 12. The ratio of these averages is  . Now, plug your original numbers into the answer choices and look for the one that equals
. Now, plug your original numbers into the answer choices and look for the one that equals  . Choice (A) gives you
. Choice (A) gives you  , which is the reciprocal of what you want. Cross it off. Choice (B) gives you
, which is the reciprocal of what you want. Cross it off. Choice (B) gives you  which is what you’re looking for. But don’t stop yet—keep checking all of the answers. Choice (D) also works with these numbers. No harm done, just try a different set of numbers and check the two remaining choices. Plug in some really unusual numbers, like 24 and 30 for a and
b, and 80 and 88 for x and y. Now you are looking for an answer to give you
which is what you’re looking for. But don’t stop yet—keep checking all of the answers. Choice (D) also works with these numbers. No harm done, just try a different set of numbers and check the two remaining choices. Plug in some really unusual numbers, like 24 and 30 for a and
b, and 80 and 88 for x and y. Now you are looking for an answer to give you 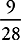 . Choice (B) no longer works, so choice (D) is your answer.
. Choice (B) no longer works, so choice (D) is your answer.
9. A, C, D, and E
The best way to approach a could be question is to consider many different kinds of numbers to plug in that could work in the problem. We will have to plug in a few times here, so let’s start with easy numbers. For
instance, let’s try making every variable in the problem equal to 1. Immediately, choices (A) and (D) work. If we made w = 1 and z = −1, then choice (E) works as well. Try plugging in 0 for either w or z and choice (C) can also work. In the end, choices (B) and (F) are always going to have a positive value on the left side of the equation and a negative value on the right, and therefore will not be correct. An absolute value is
always positive, so it can never equal something negative.
10. D and F
As soon as you see variables in the answer choices, set up your scratch paper to Plug In. Start with easy numbers like p = 2, x = 3, and y = −4. Of the answer choices, all work except choice (C), which can be eliminated. Now plug in different
numbers: Since the variables are described as non-negative and non-positive, try making p, x, and y all 0. Now choices (A), (B), and (D) all yield false statements and can be eliminated. The correct answers are choices (D) and (F).
11. D First, rewrite 0.02 as a fraction, 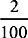 . For
. For 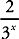 to be less than
to be less than 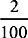 , 3x must be greater
than 100. Plugging In the Answers is the easiest way to get this right. Choice (E) is 34 = 81 and the fraction is greater than 0.02; eliminate it. Choice (D) is 35 = 243 and this makes the fraction less than 0.02. Therefore, the least value for x is 5. Be sure to answer what is asked. The inequality would be true if the denominator of
, 3x must be greater
than 100. Plugging In the Answers is the easiest way to get this right. Choice (E) is 34 = 81 and the fraction is greater than 0.02; eliminate it. Choice (D) is 35 = 243 and this makes the fraction less than 0.02. Therefore, the least value for x is 5. Be sure to answer what is asked. The inequality would be true if the denominator of 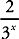 were 101,
which is choice (B); however, the question is asking for the least value of x, not of 3x, so the correct answer is choice (D).
were 101,
which is choice (B); however, the question is asking for the least value of x, not of 3x, so the correct answer is choice (D).
12. B and F
There are variables in the answer choices, so Plug In. Try x = 78. You can eliminate choices (A) and (D). Now try a weird number: 0. Eliminate choice (G). Try one more number: 156, which is double 78. This time you can eliminate choices (C) and (E). A number is
divisible by itself and a multiple of a number is divisible by that number, so the correct answers are choices (B) and (F).
13. 6 Break down the left side of the equation into prime factors to make it easier to simplify. You should get
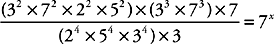
Then group all the like terms:
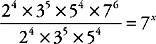
Everything cancels out on the left side except for 76, which makes 6 your answer.
![]() . Add the two fractions:
. Add the two fractions: ![]() .
.![]() . Try halving each of the values to find which one would change the
value of the expression to
. Try halving each of the values to find which one would change the
value of the expression to ![]() . Halving v to 2 works; the answer is choice (B).
. Halving v to 2 works; the answer is choice (B).![]() , and Quantity B becomes
, and Quantity B becomes ![]() . Quantity B is bigger; eliminate choices (A) and
(C). However, if you make and n = 2, then the situation is reversed: Quantity A will be
. Quantity B is bigger; eliminate choices (A) and
(C). However, if you make and n = 2, then the situation is reversed: Quantity A will be ![]() , and Quantity B will be
, and Quantity B will be ![]() . Eliminate choice (B); the answer must be choice (D).
. Eliminate choice (B); the answer must be choice (D).
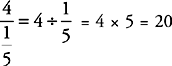 , and choice (E) is
, and choice (E) is 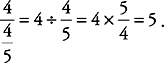 Choice (D) is the greatest.
Choice (D) is the greatest.
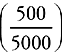 ×100, which equals the credited answer, choice (D), 10. You will arrive at the remaining, wrong answer choices if you mistakenly solve for the percent interest earned on Capital Growth Fund, and/or you represent your answer as a multiplier, rather than a percent (i.e., 0.01
versus 10%).
×100, which equals the credited answer, choice (D), 10. You will arrive at the remaining, wrong answer choices if you mistakenly solve for the percent interest earned on Capital Growth Fund, and/or you represent your answer as a multiplier, rather than a percent (i.e., 0.01
versus 10%).