Much like averages, rates, and Quant Comp Plug Ins, ratios are all about organizing your information. That means recognizing when and how to effectively use your scratch paper.
A ratio is simply a fraction. Rather than expressing a part-to-whole relationship, it expresses the relationship between two parts. The two parts combined make up the whole. If you have a bag with 5 red marbles and 4 blue marbles, your ratio of red to blue is 5 : 4. Ratios can be expressed as fractions, so you can also express the relationship as 
. Either way your total number of
marbles is 9, because 5 plus 4 is 9.
You can keep the same ratio of red to blue marbles as long as you increase your total to a multiple of 9. If you had 27 marbles total, you would have 15 red and 12 blue, but your ratio would still be 5 : 4. To keep it straight, use a ratio box.
The minute you see the word RATIO, draw a ratio box on your scratch paper.
Here’s what the ratio box looks like.
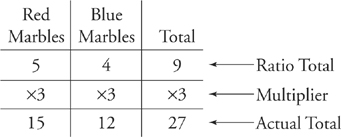
In this case you know that the ratio of red to blue marbles is 5 : 4, but the actual numbers of red and blue marbles are 15 and 12. 
of the marbles are blue, and approximately 55 percent (
) of the marbles are red. Unless a question asks for fractions of marbles, the actual total of marbles must be a
multiple of nine.
As usual, ETS will give you just enough information to fill out the chart. The question may give you the actual number of marbles, the ratio of red to blue, and then ask you for the actual number of blue marbles. Alternatively, the question may ask you what the new ratio will be if the number of blue or red marbles is increased. A really tricky question may state that some blue ones have been added, give you the new ratio, and then ask you for the actual total of red ones. No matter what is asked, a ratio is still a ratio; the ratio box will organize the information you’re given and help you get the information you need.
Sometimes you will be given a simple ratio in the form of a rate. The question may tell you the number of widgets a factory can produce in an hour, the price of one gallon of gasoline, and the speed with which a silo fills with grain. You will then have to scale this rate up or down, depending on what is asked. Alternatively, you may have to find the number of widgets the factory will produce in ten hours, the price of a 30 gallon tank of gasoline, or the percentage of the silo that will be filled in two hours. To solve these rate problems, set them up as proportions on your scratch paper, check your units, and label everything.
Example:
A digital scanner can scan five lines every second. If each line is one eightieth of an inch, how many minutes will it take to scan a 4½ inch photo?
For more practice and a more in-depth look at The Princeton Review math techniques, check out our student-friendly guidebook, Cracking the GRE.