ANSWERS

Drill 1

  1.      D

  2.      B

  3.      D

  4.      B

  5.      D

  6.      C

  7.      C

  8.      E

  9.      A

10.      B

11.      A

12.      C

13.      15

14.      C

Drill 2

  1.      C, D, G

  2.      180

  3.      30

  4.      E, F

  5.      D

  6.      B

  7.      B

  8.      B

  9.      D

10.      D

11.      D

12.      B

13.      A, B, C

EXPLANATIONS

Drill 1

  1.  D  Two parallel lines—with a line cutting through them—create big angles (bigger than 90°) and small angles (smaller than 90°). Any big angle plus any small angle equals 180°. In the figure, x appears to be a big angle and (180 – a) appears to be a small angle. So x + (180° – a) = 180°, or x = a. But in fact, because you can’t trust the figure, you don’t know whether x (and therefore a) is really a big, small, or 90° angle. The answer is choice (D).

  2.  B  Use the Rule of 180 to find r = 40 and s = 50.

  3.  D  Because ∠WXY forms a line with a 60° angle, it must be 180° – 60° = 120°; ∠WXY and ∠VXZ are vertical angles, so ∠VXZ must be 120° as well. The sum of the measures of ∠WXY and ∠VXZ is 120° + 120° = 240°.

  4.  B  The sum of c and d is 180, so you know that d + d = 180. Solve this equation: d = 100. If d = 100, then c = 80. The answer is choice (B).

  5.  D  Remember that a straight line measures 180°. Therefore, the angle inside the triangle next to the 165° angle measures 180° – 165° = 15°. A triangle contains 180° and a right angle measures 90°. The third angle in that triangle must measure 180° – (90° + 15°) = 75°. Vertical angles are equal, so x = 75. The answer is choice (D).

  6.  C  Plug in your own numbers, choosing easy values for the angle measures. If a = 40, and b = 60, then the angle in between them must measure 80° to complete the 180° in a straight line. That angle and the angle measuring co are vertical, so c = 80 as well. Both quantities then equal 100; eliminate choices (A) and (B). Try a new pair of numbers for b and c, and you will realize that plugging in any values yields the same result, making choice (C) the answer.

  7.  C  There are 180° in a straight line. The straight line is divided into six equal angles in this figure, so 180° ÷ 6 = 30°.

  8.  E  A hexagon has 6 sides. The total number of degrees in the interior of a polygon of n sides is given by (n – 2)180 = (6 – 2)180 = 720. A regular polygon is one in which the sides and angles are all equal. Dividing 720° by 6 gives you 120° for each interior angle in the hexagon. Now draw the hexagon and a point in its center. Connecting the center to each vertex divides the hexagon into six equal triangles. These segments from the center to each vertex are all of equal length, so the triangles are isosceles. These segments also bisect each of the interior angles, so the base angles of these triangles each measure 60°. Thus, the remaining angle in each triangle (near the center of the hexagon) also measures 60°, and therefore these triangles are equilateral, with sides of length 8. The area of an equilateral triangle of side x is 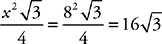. Multiplying the area of each triangle by 6 gives you ; the answer is choice (E).

  9.  A  First, solve for t: Lines a and b are parallel, so (3t + 8) + t = 180; 4t + 8 = 180; 4t = 172; t = 43. Lines a and b are parallel and you know that 2t + s = 180, so 2(43) + s = 180; 86 + s = 180; s = 94. Quantity A is greater.

10.  B  If f = 130, then both large angles formed by lines t and k also measure 130°. The small angles formed by those two lines therefore measure 50° (notice that one of these angles is the left base angle of the triangle). If g = 70, then the angle above it (the other base angle of the triangle) must measure 110° to complete the 180° in a straight line. So far, you have 160° in the triangle. To complete the 180° total in the triangle, h must measure 20°. The answer is choice (B).

11.  A  The angle between the ones marked xo and 3xo is vertical to the one that measures 4yo. These three angles form a straight line, so x + 4y + 3x = 180. Since 4y = 5x, x + 5x + 3x = 180; 9x = 180; x = 20. Therefore 4y = 5x = 100; y = 25.

12.  C  Plug in values for the unknown angles. When a = 60 and b = 130, the angle vertical to a also measures 60°, and the angle adjacent to b within the triangle must measure 180° – 130° = 50°. The sum of the angles in a triangle is 180°. Therefore, the remaining angle measures 180° – 60° – 50° = 70°. Angle c is vertical to the 70° angle, so c = 70. Quantity A is 60 + 70 = 130 and Quantity B is 130; the quantities are equal. Eliminate choices (A) and (B). Plugging in a second set of numbers will show you that any set of numbers yields the same result, so the answer is choice (C). Alternatively, you could use algebra to determine that the three angles in the triangle measure ao, (180 – b)o, and co. Therefore, a + (180 – b) + c = 180. Subtract 180 from each side of this equation and add b to each side; a + c = b. The quantities are equal.

13. 15 The formula for the total interior angles of a polygon with n sides is (n – 2)180, so the interior angles of an 8-sided polygon total 6 × 180 = 1080°. Since it’s a regular polygon, divide that total by the 8 angles to determine that p = 135 when n = 8. For the 6-sided polygon, the total of the interior angles is 4 × 180 = 720°, and each angle is 720 ÷ 6 = 120. Thus p = 120 when n = 6, and 135 – 120 = 115.

14.  C  Use the laws of parallel lines to fill in the diagram. ∠ABD + ∠BDE + ∠CDE = 180° because lines AB and CD are parallel. ∠CDE = 180° – x° – 44°. Therefore, 3x + 2x + 180 – x – 44 = 180. Solving for x gives you 11, and ∠ABD = 33°.

Drill 2

  1.      C, D, and G
Remember that when a line intersects two parallel lines, it makes large and small angles; all of the large angles are equal, as are all of the small ones. In this case, s is equal to the other large angle measures: v, w, and z. Choices (C), (D), and (G) work.

  2. 180 You don’t actually have to do any math for this question. When parallel lines intersect, any big angle plus any little angle is 180°; since x is a little angle and y is a big angle, the sum must be 180. However, you could also use the rules regarding opposite and corresponding angles, or the parallelogram rules, with the 75° in the corner. In this case, x = 75 and y = 105, so 75 + 105 = 180.

  3. 30 If you draw a line down from B to the base of the figure, you can subtract the 90° that are left over from the 150° angle and you’ll have 60° left. This makes a 30-60-90 triangle with vertex D. And if ∆CED is isosceles, that makes angle CED 30° as well.

  4.  E  and F Because they are supplementary angles, a + b = 180. So subtract the range of values for a from 180 to get 116 < b < 150. You know that b and d are equal, so double b to get 232 < b + d < 300. Only choices (E) and (F) fall within this range. (You could also Plug In the Answers on this question.)

  5.  D  The total number of degrees in a hexagon is 720; if you don’t know the formula, (s – 2) × 180, you can divide the hexagon into 4 non-overlapping triangles. Subtract the two known angles, leaving you with 508° for the four remaining angles. Since the remaining angles are equal, each angle is 508 ÷ 4 = 127°.

  6.  B  It’s a geometry problem with variables in the answer choices, so draw the figure and set up your scratch paper to Plug In. Try x = 60 and y = 70; the missing angle in the small triangle on top is now 50°, as is the missing angle in the small triangle in the middle. Since z combines with the 2 angles you just found to form a line, 2(50) + z = 180, and z = 80. The problem asked for the sum of x and y, so plug 80 in for z to all the answers and look for your target answer of 130. Only choice (B) works.

  7.  B  The question is asking for a specific amount and there are no variables in the answer choices, so PITA. Starting with choice (C), b = 60. By vertical angles, b = 2a, so a = 30. If a = 30, then ∠SWU = 90. This won’t work because all four angles of a square equal 90° and ∠SWU must be smaller than 90. Eliminate choices (C), (D), and (E). Try a smaller value, such as in choice (B). Now b = 40 which means a = 20, ∠SWU = 60 and ∠UWV is 30°. A right triangle in which the hypotenuse is twice one of the sides is a 30:60:90 triangle. That means that triangle UWV is a 30:60:90 triangle in which ∠VUW is 60° and ∠UWV is 30°. Per our calculations, that’s what ∠UWV is supposed to be, so the correct answer is choice (B).

  8.  B  Fill in the diagram little by little. Angle LON must be equal to 75 degrees, because ∠LON + 115° = 180° to make a straight line. The shape is a parallelogram, so it must also be true that ∠LON = ∠LMN. There are 360 degrees in the whole parallelogram, and ∠LON + ∠LMN = 150, so there are 360 – 150 = 110 degrees remaining in the parallelogram. Thus, (x + 10) + (y + 8) = 110. You can now simplify the expression to get x + y = 92.

  9.  D  For this problem it helps to draw the figure. When you do, exaggerate the angles as shown in the diagram below. From the diagram, ∠ACE and ∠BCD are both smaller than 90°. The sum of any two angles less than 90° will be less than 180°; this sum is x from the question, making choice (D) correct. You can also plug in your own numbers to the diagram to test the choices. If ∠ACD is 120°, then ∠ACD and ∠BCD are both 60° and add up to 120°, which is now the value of x. You can eliminate choices (A) and (E). To eliminate further, try a really big number such as 170° for ∠ACD Angles ∠ACE and ∠BCD are now both 10° and add up to 20°, the new value of x. You can eliminate choices (B) and (C), leaving choice (D) as the correct answer.

10.  D  As soon as you see variables in the answer choices, draw your figure and set up your scratch paper to Plug In. The sum of d, e, and f has to be 180, so try d = 50, e = 60, and f = 70. Similarly, the sum of a, b, and c has to be 360, so try a = 110, b = 120, and c = 130. Since the problem asked for a + b + f, your target answer is 110 + 120 + 70 = 300. Now plug your values for c, d, and e into the answer choices; only choice (D) hits your target.

11.  D  To solve this question, plug in some easy values for the variables. For example, if the polygon were a square, then x = 4. Since each angle would equal 90, q = 90, your target answer. Check all the answers by plugging in x = 4. Only 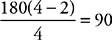, so choice (D) is correct.

12.  B  To answer this question, Plug In the Answers. Because 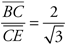, triangle BCE is a 30:60:90 triangle and BCD is an equilateral triangle with all angle measures equal to 60. Start with choice (C). If ∠CAD = 30, then since triangle ACD is isosceles, ∠CAB =30 as well. Since both triangles ABC and ACD share 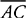, and triangle ABC is isosceles, then ∠CAB and ∠CBA are both equal to 30 as well. The angles within triangle ABD should add up to 180. However, ∠CAD + ∠CAB + ∠CDA + ∠CDB + ∠CBD + ∠CBA =30 + 30 + 30 + 60 + 60 + 30 = 240, which is too big; eliminate choices (C) and (D), which is bigger. Now try choice (B). If ∠CAD = 15, then ∠CDA = 15 as well, and ∠CAB and ∠CBA are both equal to 15 as well. Verify that the angles will add up to 180 for triangle ABD: ∠CAD + ∠CAB + ∠CDA + ∠CDB + ∠CBD + ∠CBA =15 + 15 + 15 + 60 + 60 + 15 = 180. Choice (B) is the correct answer.

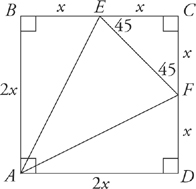
13.      A, B, and C
To solve this question, draw and label the figure. When drawn and labeled, the figure should look like this:

Since points E and F are midpoints of the sides of a square and ∠C is a right angle, triangle ECF is a 45:45:90 triangle; thus choice (A) must be correct. Since ∠CEF = 45°, if ∠FEA also equaled 45, then ∠CEA would be a right angle and would be perpendicular to ; instead, since ∠FEA + 45 > 90, then ∠FEA > 90 and choice (B) must be correct. If ∠EFA = 90, then ∠FEA = 90, and thus ∠EAF = 0; since ∠EAF > 0, ∠EFA < 90, so choice (C) must be correct. If ∠FAD = 30, then triangle FAD would be a 30:60:90 right triangle with legs of x and and a hypotenuse of 2x; since that is not the case, ∠FAD ≠ 30; eliminate choice (D). If ∠AEB = 60, then triangle EAB would be a 30:60:90 right triangle with legs of x and and a hypotenuse of 2x; since that is not the case, ∠AEB ≠ 60; eliminate choice (E). If ∠AFD = 45, then ∠FAD = ∠EAB = 45, which would mean that ∠EAF = 0; since ∠EAF > 0, ∠AFD cannot = 45; eliminate choice (F).