1. C The answer asks for 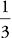 of the whole volume, so begin by dividing the height of the trunk by 3 to find the volume of one of the sections of the trunk:
of the whole volume, so begin by dividing the height of the trunk by 3 to find the volume of one of the sections of the trunk: 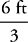 = 2ft. The volume formula for a cylinder is: V= πr2h = π × 22 × 2= 8π.
= 2ft. The volume formula for a cylinder is: V= πr2h = π × 22 × 2= 8π.
2. B Three times the surface area of a cube with edge length of 1 cm is three times the area of each square face times the number of faces: 3 × (1 cm × 1 cm) × 6 faces = 18 cm2. The surface area of a cube with edge length of 3 cm is (3 cm × 3 cm) × 6 faces = 54 cm2. Quantity B is greater.
3. A The diagonal of a square is always longer than its side, so half a diagonal—segment AE—must be longer than half a side. Half the length of a side of this square is 4. Therefore, AE is larger than 4.
4. A Plug in a value for n: Try n = 3. If each edge of the cube is 3, AB = DE = 3, and because the diagonal of a square forms two 45-45-90 triangles, BD = AE = 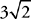 . The total perimeter is
. The total perimeter is 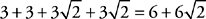 . Now plug in 3 for n in the answer
choices; only choice (A) hits your target.
. Now plug in 3 for n in the answer
choices; only choice (A) hits your target.
5. A Draw it! You should end up with two squares oriented the same way touching at C. The squares have the same area, so their sides must be the same length. Plug in a side length for the squares to simplify the comparison—try 2. A square cut in half along its diagonal yields a pair of 45-45-90 triangles, so these two squares with sides of 2 each have diagonals of 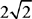 . Diagonals AC and CE connect to form segment AE. Quantity A is 3 × 2 = 6, and Quantity B is
. Diagonals AC and CE connect to form segment AE. Quantity A is 3 × 2 = 6, and Quantity B is 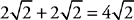 Quantity A is greater.
Quantity A is greater.
6. B You will be subtracting the volume of the cylinder from that of the cube, so the answer will contain π; eliminate choices (A) and (E). To find the volume of the figure, start with the volume of the cube: V= s3= 93 = 729. The formula for volume of a cylinder is V = πr2h. The cylinder runs the length of the cube, so its height is the same as the length of the cube’s edge, 9. Next, find the radius. The length of diagonal AB is 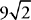 (remember your special triangles—this is a 45-45-90 triangle!). The points between A and B are equally spaced, so the length of CD, the circle’s diameter, is
(remember your special triangles—this is a 45-45-90 triangle!). The points between A and B are equally spaced, so the length of CD, the circle’s diameter, is 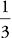 the length of AB,
the length of AB, 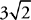 . The radius is 1/2 the diameter, or
. The radius is 1/2 the diameter, or 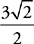 . Plug the radius and the height into the formula:
. Plug the radius and the height into the formula: 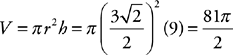 . Subtract this from the cube’s volume for a final answer of
. Subtract this from the cube’s volume for a final answer of 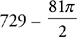 .
.
7. A First, write out your formulas and draw a figure. The volume of a cube is V = s3 = 512, giving you s = 8. The surface area of a cube is 6 times the area of each square face of the cube (SA = 6s2), therefore, 6 × 82 = 384.
8. A The surface area of a cube is 6 times the area of each square face of the cube (SA = 6s2), or 54 = 6s2. So each side is 3. The diagonal of the square forms the hypotenuse of a right triangle. Remember that the hypotenuse of a right triangle is always longer than either leg. Therefore, the diagonal is larger than 3.
9. A A cube has 6 identical faces, each with an area of s2, so the surface area of a cube is 6s2; the volume of a cube is s3. Quantity A is 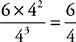 , and Quantity B is
, and Quantity B is 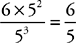 . Quantity A is greater.
. Quantity A is greater.
10. D First, eliminate choices (A) and (B) because the volume must increase when the side of the square base increases. Next, set up a proportion using the square base of the prism: 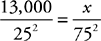 . Finally, cross-multiply and solve for x to get choice (D).
. Finally, cross-multiply and solve for x to get choice (D).
11. B Try plugging in a value for the depth, 2 feet. Note that the radii are half the given diameters. Therefore, the volume of water held by Marty’s pool is V = πr2h = π(6)2(2) = 72π and the volume of water held by Rusty’s pool is V = πr2h = π
(9)2(2) = 162π. Dividing 162π by 72π yields 2.25.
12.  First, find the angle measures. Since AC and AB are radii of the circle, the triangle they form along with BC must be isosceles. Let the small angles, ∠ACB and ∠ABC, be x, which makes ∠BAC equal to 4x; now 4x + x +
x = 180, so x = 30 and ∠BAC must be 120˚. At this point, you’re essentially done: Though there’s other information in the problem about diameters and heights and so on, it’s all unnecessary. Since ∠BAC represents
First, find the angle measures. Since AC and AB are radii of the circle, the triangle they form along with BC must be isosceles. Let the small angles, ∠ACB and ∠ABC, be x, which makes ∠BAC equal to 4x; now 4x + x +
x = 180, so x = 30 and ∠BAC must be 120˚. At this point, you’re essentially done: Though there’s other information in the problem about diameters and heights and so on, it’s all unnecessary. Since ∠BAC represents  , or
, or 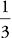 , of the circular base,
the shaded represents the same fraction of the entire cylinder.
, of the circular base,
the shaded represents the same fraction of the entire cylinder.
13. A, B, D, and F
First, find the dimensions of the cylinder. Because the cylinder’s height is 20 and its volume is 980π, and V = πr2h, 980π = π (r2)(20), and r = 7. The diameter of the cylinder is 14. Because the end of the
cylinder is a circle with a diameter of 14, the largest box that could fit in the cylinder would have a square base with a diagonal of 14. Using the Pythagorean theorem, you can find that the length and the width of the largest possible box equal 14 divided by 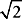 , or approximately 9.90. Therefore, the box’s length and width must each be less than 10, and its height may be up to 20. Choices (A), (B), (D), and (F)
match these criteria and work as the dimensions of the box.
, or approximately 9.90. Therefore, the box’s length and width must each be less than 10, and its height may be up to 20. Choices (A), (B), (D), and (F)
match these criteria and work as the dimensions of the box.
1. 505 To find the number of cylinders that can be made from one block of steel, divide the volume of the block by the volume of a cylinder. Start by converting the dimensions of the block into inches: Each steel block is 24 inches by 144 inches by 180 inches, so the volume is 24 × 144 × 180 = 622,080. The formula for the volume of a cylinder is V = πr2h, so the volume
of each cylinder is π × 72 × 8 = 1230.88. Finally, 622,080 ÷ 1230.88 = 505.395; the problem asked for complete cylinders, so the correct answer is 505.
2. C It’s a geometry problem with variables in the answer choices, so draw the figure and set up your scratch paper to Plug In. Plug in an easy number like r = 5; label the radius 5 and the height 15, which is 1.5 times your diameter of 10. The surface area of a cylinder is made up of 3 smaller areas: 2 identical circular bases on top and bottom, and a rectangle that’s the height
of the cylinder on one side and the circumference of the base on the other. If r = 5, then the area of each base is 25π, or 50π for the 2 of them. The rectangle is 15 × 10π = 150π, so the total surface area is 200π, your target answer. Plug 5 in for r in the answers, and only choice (C) matches your target answer of 200π.
3. 84 Use the formula for the volume of a cube to find the length of each side: V = s3, so 64 = s3, and s = 4. To find the surface area of a cube, find the area of each face of the cube and multiply by 6: Each side is 4, so each face has an area of 4 × 4 = 16, and the total surface area of the cube is 16 × 6 = 84.
4. A, B, C, D, and E
If the diagonal were exactly 10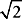 , then the side of the cube would be 10. Because the diagonal is less than 10
, then the side of the cube would be 10. Because the diagonal is less than 10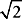 , each side is less than 10. Therefore, the volume must be less than 103, or 1,000. Any
value less than 1,000 is correct.
, each side is less than 10. Therefore, the volume must be less than 103, or 1,000. Any
value less than 1,000 is correct.
5. A and B Plug in the answers to your on-screen calculator. When cubed, choices (A) and (B) are less than 2 cubic feet. The other three choices for the edge of the box produce volumes over 2 cubic feet.
6. 704 Because the cylinder’s height is 11 and its volume is 176π, and V = πr2h, 176π = π(r2)(11), and r = 4. The diameter of the cylinder is 8. The box will need a length of 8 and a width of 8 to accommodate the base of the cylinder, and a height of 11. The volume of the
smallest box will equal 8 × 8 × 11, or 704.
7. D Because all the edges are equal, the figure is a cube. The formula for the surface area of a cube is 6s2, where s is a side of the cube. Thus, the surface area of the solid is 337.5; eliminate choice (A). The formula for the volume of a cube is s3, so the volume of the cube is 421.875; eliminate choice (B). WT is a
diagonal of the cube. The formula for the diagonal of a box is a2 + b2 + c2 = d2, where a, b, and c are the sides of the box and d is the diagonal. Thus, WT is 12.99 and does not equal UT. Eliminate choice (C). VS is also a diagonal of the cube, so its length is 12.99. The only correct
answer is choice (D).
8. E Draw a rectangular box. The longest distance between any two corners is going to be the box’s three-dimensional diagonal from a bottom corner to the top corner furthest away. You can solve this problem by using the Super Pythagorean theorem a2 + b2 + c2 = d2. 232 + 292 + 372 = 2,739 = d2. The square root is a little more than 52.
9. 4,175 Calculate the surface area of each side of the box. Two sides are each: 29 × 37 × 2 = 1,073 square inches. Two other sides are 29 × 47 × 2 = 1,363 square inches. The last two sides are 37 × 47 × 2 = 1,739 square inches. The sum of the six sides is 4,175.
10. D The volume formula for a cube is V = s3, so a volume of 125 yields a side of 5. One face therefore has an area of 25, and the total area of 2 faces is 50. If you selected choice (C), you may have found the perimeter rather than the area. If you selected choice (B), you may have forgotten to find the total for 2 faces, and if you selected choice (A), you may have done both.
11. E The distance from C to F is the diagonal of the box, so use the Super Pythagorean theorem: a2 + b2 + c2 = d2, where a, b, and c are the sides of the box and d is the diagonal. You have the length and height of the box, so use the
volume formula to find the width: 720 = (15)(6)w, so the width is 8. Now plug your numbers into the formula: 152 + 82 + 62 = d2, so 325 = d2, and d = 18.03.
12. 5.5 The volume of a cylinder = πr2h. Since the height equals the diameter: 332.75π = π(r2)(2r). Solving for r gives you 5.5 as the final answer
13. D First, find the volume of the entire box, which equals 6 × 8 × 5 = 240. Solve for the volume of the three-dimensional triangular shape on top and subtract it from the total volume to find the volume of the shaded part. The triangular shape has known dimensions of 8 by 5. The third dimension ranges based on the length of AE, with 3 < AE < 4 because AE has to
be bigger than EB. Therefore, the triangular shape’s volume falls between one-half of 8 × 5 × 3 = 60 and one-half of 8 × 5 × 4 = 80. The shaded area’s volume falls between 240 – 80 = 160 and 240 – 60 = 180. Only choice (D) works.
![]() of the whole volume, so begin by dividing the height of the trunk by 3 to find the volume of one of the sections of the trunk:
of the whole volume, so begin by dividing the height of the trunk by 3 to find the volume of one of the sections of the trunk: ![]() = 2ft. The volume formula for a cylinder is: V= πr2h = π × 22 × 2= 8π.
= 2ft. The volume formula for a cylinder is: V= πr2h = π × 22 × 2= 8π.![]() . The total perimeter is
. The total perimeter is ![]() . Now plug in 3 for n in the answer
choices; only choice (A) hits your target.
. Now plug in 3 for n in the answer
choices; only choice (A) hits your target.![]() . Diagonals AC and CE connect to form segment AE. Quantity A is 3 × 2 = 6, and Quantity B is
. Diagonals AC and CE connect to form segment AE. Quantity A is 3 × 2 = 6, and Quantity B is ![]() Quantity A is greater.
Quantity A is greater.![]() (remember your special triangles—this is a 45-45-90 triangle!). The points between A and B are equally spaced, so the length of CD, the circle’s diameter, is
(remember your special triangles—this is a 45-45-90 triangle!). The points between A and B are equally spaced, so the length of CD, the circle’s diameter, is ![]() the length of AB,
the length of AB, ![]() . The radius is 1/2 the diameter, or
. The radius is 1/2 the diameter, or ![]() . Plug the radius and the height into the formula:
. Plug the radius and the height into the formula: 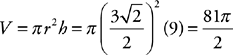 . Subtract this from the cube’s volume for a final answer of
. Subtract this from the cube’s volume for a final answer of ![]() .
.![]() , and Quantity B is
, and Quantity B is ![]() . Quantity A is greater.
. Quantity A is greater.![]() . Finally, cross-multiply and solve for x to get choice (D).
. Finally, cross-multiply and solve for x to get choice (D).![]() First, find the angle measures. Since AC and AB are radii of the circle, the triangle they form along with BC must be isosceles. Let the small angles, ∠ACB and ∠ABC, be x, which makes ∠BAC equal to 4x; now 4x + x +
x = 180, so x = 30 and ∠BAC must be 120˚. At this point, you’re essentially done: Though there’s other information in the problem about diameters and heights and so on, it’s all unnecessary. Since ∠BAC represents
First, find the angle measures. Since AC and AB are radii of the circle, the triangle they form along with BC must be isosceles. Let the small angles, ∠ACB and ∠ABC, be x, which makes ∠BAC equal to 4x; now 4x + x +
x = 180, so x = 30 and ∠BAC must be 120˚. At this point, you’re essentially done: Though there’s other information in the problem about diameters and heights and so on, it’s all unnecessary. Since ∠BAC represents ![]() , or
, or ![]() , of the circular base,
the shaded represents the same fraction of the entire cylinder.
, of the circular base,
the shaded represents the same fraction of the entire cylinder.![]() , or approximately 9.90. Therefore, the box’s length and width must each be less than 10, and its height may be up to 20. Choices (A), (B), (D), and (F)
match these criteria and work as the dimensions of the box.
, or approximately 9.90. Therefore, the box’s length and width must each be less than 10, and its height may be up to 20. Choices (A), (B), (D), and (F)
match these criteria and work as the dimensions of the box.