1. D When solving algebraically, be careful to perform the same operation on both sides of the equation: 4c + 6 = 26, so subtract 6 from both sides to find 4c = 20 and c = 5. Therefore, 3c – 2 = (3 × 5) – 2 = 13.
2. C You can find the two quantities to be equal by plugging in values for k and j: If k = 2 and j = 3, then Quantity A is  , or
, or 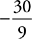 , which can be reduced to
, which can be reduced to 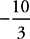 ; Quantity B is
; Quantity B is 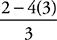 , or
, or 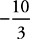 . Algebraically, try factoring and canceling a 3 out of the numerator of Quantity A:
. Algebraically, try factoring and canceling a 3 out of the numerator of Quantity A: 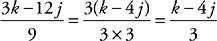 .
.
3. A Start by substituting the given values for the variables in the equation. You’ll be left with (–5 − 5)(5 + 5), which simplifies to (–10)(10), or –100.
4. A Solve the given equation by multiplying both sides of the equation by 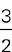 . You get a value of
. You get a value of 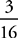 for y. Then use the Bowtie method to
compare the fractions in the quantities; the fraction in Quantity A is greater.
for y. Then use the Bowtie method to
compare the fractions in the quantities; the fraction in Quantity A is greater.
5. A To solve this single-variable equation, you’ll just need to isolate the variable. First, add 24 to both sides to yield 7a + 32 = 8a. Then subtract 7a from both sides to yield 32 = a. Quantity A is greater.
6. D Since there are variables in the question and answer choices, Plug In for x. Try x = 3. This gives you 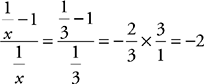 . Check all 5 answers. Only choice (D) works.
. Check all 5 answers. Only choice (D) works.
7. A You know that b is greater than a, so (a – b) will always be negative, and Quantity A will always be greater. Alternatively, you can solve this one by plugging in values for a and b. Try making a =  and b=
and b= : The value in Quantity B is now
: The value in Quantity B is now  . Quantity A is greater, so eliminate choices (B) and (C).
. Quantity A is greater, so eliminate choices (B) and (C).
8. C Solve this “must be” problem by plugging in values for a and b. Starting with the simplest allowable values, a = 30 and b = 15, does not eliminate any answer choices. Next, try a = 100 and b = 0; now choices (A), (B), and (D) can be
eliminated. Finally, try a = 30 and b = –30; now choice (E) can be eliminated, leaving only choice (C), which is the correct answer.
9. 20 Since Lyle bought an equal number of CDs at each price, combine the prices: 1 CD of each type would cost $8 + $12 = $20. For a total of $200, then, Lyle bought 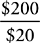 = 10 CDs of each type, for a total of 20 CDs altogether.
= 10 CDs of each type, for a total of 20 CDs altogether.
10. A The given inequality is equivalent to 3x – 27 < 11x – 2, which becomes –8x < 25. Dividing both sides by –8 (and flipping the inequality sign), you get x >  . Therefore, any number that is greater than
. Therefore, any number that is greater than 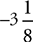 will satisfy the inequality, so the greatest integer that does not satisfy it is x = –4, choice (A).
will satisfy the inequality, so the greatest integer that does not satisfy it is x = –4, choice (A).
11. D Replace y with 4 to get 16 + 4a + 8 = 36. Then solve the equation to find that a equals 3.
12. D Start by combining the 2 given equations: If a = 4 and 6 < b < 8, then the acceptable range for  is
is  , which can be reduced to
, which can be reduced to
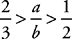 or, in decimal form, 0.5 <
or, in decimal form, 0.5 <  < 0.67. Select choice (D) because
< 0.67. Select choice (D) because  can be either larger or smaller than 0.6.
can be either larger or smaller than 0.6.
13. A The problem has variables in the answer choices so Plug In. Because the problem says, “in terms of a,” a is the variable that you want to plug in for. If a = 8, then b = 2, and that is now your target. When you plug in your value for a into choice (B), you
get 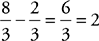 ; thus, the correct answer.
; thus, the correct answer.
14. D Try plugging in values for a and c. Let a = 6 and c = 2. Then b= 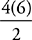 =3. If a is halved, equal it will 3. If c is doubled, it will equal 4. So now, b=
=3. If a is halved, equal it will 3. If c is doubled, it will equal 4. So now, b=  =3. Because the question is looking for a percentage decrease, apply the percentage change formula:
=3. Because the question is looking for a percentage decrease, apply the percentage change formula:  .
.
15. C Plug In The Answers starting with choice (C). Choice (C) yields 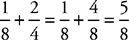 , so it’s the correct answer.
, so it’s the correct answer.
16. D First, plug in 1 for the number of boxes of chocolate chip cookies. In Quantity A, if Sally buys 1 box of chocolate chip cookies, then she buys 2(1) + 3 = 5 boxes of oatmeal cookies, for a total of 6 boxes, or 36 cookies. In Quantity B, if Sally buys 1 box of chocolate chip cookies, then she buys 3(1)
– 2 = 1 box of oatmeal cookies, for a total of 2 boxes, or 12 cookies. Quantity A is greater, so eliminate choices (B) and (C). Now plug in 10 boxes of chocolate chip cookies: Quantity A is now 2(10) + 3 = 23 boxes of oatmeal cookies, for a total of 33 boxes, or 198 cookies, and Quantity B is now 3(10) – 2 = 28 boxes of oatmeal cookies, for a total of 38 boxes, or 228 cookies. Quantity B is now greater, so eliminate choice (A), and you’re left with choice
(D).
1. B You know that 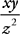 , so solve this one by plugging in values for z, x, and y. If x = 12, then z = 36 and y = 144;
, so solve this one by plugging in values for z, x, and y. If x = 12, then z = 36 and y = 144;  . The correct answer is choice (B).
. The correct answer is choice (B).
2. A Use the information in the problem to write the equations x + y = 27 and  + x=y. You can combine these two equations to say that
+ x=y. You can combine these two equations to say that  =x+x=27. When you solve this new equation you find that x = 12. You can then go back to your first equation and find that y = 15. The positive difference between 15 and 12 is 3, so select choice (A).
=x+x=27. When you solve this new equation you find that x = 12. You can then go back to your first equation and find that y = 15. The positive difference between 15 and 12 is 3, so select choice (A).
3. 8 First, factor the quadratic: (2x + 2)(x – 3) = 0. Next, solve for each solution (root). If 2x + 2 = 0, then x = –1. If x – 3 = 0, then x = 3. The sum of the roots is 2, and twice their sum is 4. The factors of 4 are 1, 2, 4, and the
product of those factors is 8, the final answer.
4. A The problem contains the phrase “must be,” so try to find numbers to plug in that disprove four of the five answer choices. If a = 4 and ab = –12, then b = –3; eliminate choices (B), (D), and (E). Now determine whether b must be an
integer. If a = 4 and ab = –2, then b =  ; eliminate choice (C), and you’re left with choice (A), the correct answer.
; eliminate choice (C), and you’re left with choice (A), the correct answer.
5. D If a range of values for a can be found, then the range of values for a2 can be found. Start by testing the end values of b, –3 and 1. Plug in –3 for b in the first given inequality then solve for a. You find that –4
< a < 7. If b = 1, 0 < a <11; b could be any integer in the range –3 ≤ b ≤ 1, this means –4 < a < 11 overall. Remember to take the last step, though! The question is looking for the range of a2, not a; a2 is always positive (i.e., 0 < a2).
Because a < 11, a2 < 121. This means 0 < a2 < 121; the answer is choice (D).
6. D Know your common quadratics. You are asked for the value of x + y. Because x2 − y2 = (x + y)(x − y) = 24, if the value of (x − y) is found,
(x + y) can be figured out. Manipulate the equation 0.5(y − x) = –1 to get (y − x) = –2. Multiplying both sides by –1, you get x – y = 2. Substitute this value into the equation (x + y)(x – y) = 24 and then divide both sides of the equation by 2 to get (x + y) = 12. The answer is choice (D).
7. C Translate what you are told into algebra:  =2 and
=2 and 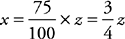 . Notice that the problem then tells you that z is
. Notice that the problem then tells you that z is  larger than w, not z is
larger than w, not z is  of w. That means
of w. That means 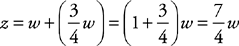 . At this point, you can either Plug In or do algebra. To Plug In, choose 4 for w, so z = 7, and
. At this point, you can either Plug In or do algebra. To Plug In, choose 4 for w, so z = 7, and 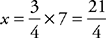 . If
. If  =2, then x = 2y, so
=2, then x = 2y, so  =2y; y=
=2y; y= . Now plug
. Now plug 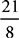 into the answer
choices for y to see which hits your target number, w = 4. Only choice (C) does. Alternatively, to do algebra, combine the first two equations you translated into algebra: 2y=
into the answer
choices for y to see which hits your target number, w = 4. Only choice (C) does. Alternatively, to do algebra, combine the first two equations you translated into algebra: 2y= z; z=
z; z= y. Combining this equation with the one you derived above, it follows that
y. Combining this equation with the one you derived above, it follows that  y=
y= w, and w=
w, and w=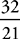 y; the answer is choice (C).
y; the answer is choice (C).
8. C Translate what you are told into algebra: 2 ≤ x + y ≤ 5 and 0 ≤ 2x + 3y ≤ 40. By manipulating the inequalities, you find that 2 − y ≤ x ≤ 5 – y and –2x ≤ 3y
≤ 40 − 2x. Substitute the endpoints of the values of x into the second inequality: –2(2 – y) ≤ 3y ≤ 40 − 2(2 − y) and –2(5 − y) ≤ 3y ≤ 40 − 2(5 − y). By solving for y, the first range yields –4 ≤ y ≤ 36, and the second yields –10 ≤ y ≤ 30,
meaning –10 ≤ y ≤ 36 overall.
9. C Using the Bowtie method, you find that  =6. By multiplying both sides of the second equation by
=6. By multiplying both sides of the second equation by  , you find that
, you find that  . Flipping both fractions yields
. Flipping both fractions yields  =6, and thus,
=6, and thus, 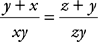 . Inspecting the two fractions, you may realize that z must equal x. Alternatively, by applying the Bowtie again, you obtain (y + x)(zy) = (z +
y)(xy), and thus zy2 + xyz = xyz + xy2, meaning zy2 = xy2, or z = x, so the answer is choice (C).
. Inspecting the two fractions, you may realize that z must equal x. Alternatively, by applying the Bowtie again, you obtain (y + x)(zy) = (z +
y)(xy), and thus zy2 + xyz = xyz + xy2, meaning zy2 = xy2, or z = x, so the answer is choice (C).
10. B By rearranging the first two equations, you obtain c = 7 – ab and b = 5 − ac. By substituting these relationships into the third equation, a + (5 − ac) + (7 − ab) = 6 is obtained. Manipulating the equation yields a −
ac − ab + 12 = 6, or a − a (c + b) + 6 = 0. Since a + b + c = 6, b + c = 6 − a. Substituting this into the previous equation yields a − a (6 − a) + 6 = a − 6a + a2 + 6 = 0, or a2 − 5a + 6 = 0. Factoring
and finding the roots gives you a = 2 or a = 3. If a = 2—by substituting the value back into the equations—then b = 2 and c = 1. If a = 3, then b = 3 and c = 1. You are looking for abc, and either way, the value is 3 × 2 × 1 = 6. The answer is choice (B).
11.
12
You are being asked to subtract the a and b terms. Be careful that you don’t just combine the largest value of a with the largest value of b to get a – b = 9 – 2 = 7, the wrong answer. When you combine inequalities, you have to make four calculations to check the four possibilities. Subtract the smallest values of a and b: –4 – (–3) = –1.
Subtract the largest values of a and b: 9 – 2 = 7. Subtract the smallest value of a and the largest value of b: –4 – 2 = 6. Subtract the largest value of a and the smallest value of b: 9 – (–3) = 12. Of the four possible values above, the greatest possible value is 12.
12. C and E Try plugging in values for m and n to the inequality in the question. If m = 5 and n = 1, both numbers are integers, so choices (A) and (B) work as do all of the other choices. But what if m and n are negative decimals, say –2.3 and
–6.3? Then choices (A) and (B) don’t work, since neither number is an integer; eliminate them. Choice (C) still works. Choice (D) is out, since the sum of the two numbers is negative, but the difference is positive, leaving choice (E) in. Choices (F) and (G) also still work. However, by switching m to a positive value, such as 5, you can knock out choices (F) and (G). Only choices (C) and (E) will work no matter what numbers you plug in.
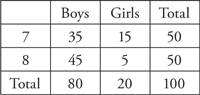
13. 35
Wouldn’t this be a lot easier if you knew how many students there are? The question doesn’t say, so plug in your own number. The question deals in percentages, so let’s say there are 100 students in the class. That means that there are 80 boys and 20 girls, and 50 students who are 7 and 50 students who are 8. 25 percent of 20 is
5, which leaves 15 girls who are 7. Subtract 15 from 50 and you are left with 35 boys who are 7. You can also employ the group grid.
![]() , or
, or ![]() , which can be reduced to
, which can be reduced to ![]() ; Quantity B is
; Quantity B is ![]() , or
, or ![]() . Algebraically, try factoring and canceling a 3 out of the numerator of Quantity A:
. Algebraically, try factoring and canceling a 3 out of the numerator of Quantity A: ![]() .
.![]() . You get a value of
. You get a value of ![]() for y. Then use the Bowtie method to
compare the fractions in the quantities; the fraction in Quantity A is greater.
for y. Then use the Bowtie method to
compare the fractions in the quantities; the fraction in Quantity A is greater.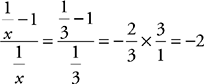 . Check all 5 answers. Only choice (D) works.
. Check all 5 answers. Only choice (D) works.![]() and b=
and b=![]() : The value in Quantity B is now
: The value in Quantity B is now ![]() . Quantity A is greater, so eliminate choices (B) and (C).
. Quantity A is greater, so eliminate choices (B) and (C).![]() = 10 CDs of each type, for a total of 20 CDs altogether.
= 10 CDs of each type, for a total of 20 CDs altogether.![]() . Therefore, any number that is greater than
. Therefore, any number that is greater than ![]() will satisfy the inequality, so the greatest integer that does not satisfy it is x = –4, choice (A).
will satisfy the inequality, so the greatest integer that does not satisfy it is x = –4, choice (A).![]() is
is ![]() , which can be reduced to
, which can be reduced to
![]() or, in decimal form, 0.5 <
or, in decimal form, 0.5 < ![]() < 0.67. Select choice (D) because
< 0.67. Select choice (D) because ![]() can be either larger or smaller than 0.6.
can be either larger or smaller than 0.6.![]() ; thus, the correct answer.
; thus, the correct answer.![]() =3. If a is halved, equal it will 3. If c is doubled, it will equal 4. So now, b=
=3. If a is halved, equal it will 3. If c is doubled, it will equal 4. So now, b= ![]() =3. Because the question is looking for a percentage decrease, apply the percentage change formula:
=3. Because the question is looking for a percentage decrease, apply the percentage change formula: ![]() .
.![]() , so it’s the correct answer.
, so it’s the correct answer.