ANSWERS
Drill 1
Drill 2
Drill 3
Drill 4
EXPLANATIONS
Drill 1
1. D To find the average, add up the values and divide by 2: 
. You can also Plug In on this one. If y = 3, then 
= 17, your target number.
Only choice (D) hits the target.
2. C The average is the sum divided by the number of items. Both ask for the average of three numbers. The sum of the three numbers in both quantities is 84, so their averages must be equal.
3. A The mean is found by dividing the sum of the elements by the number of elements. In this case: 2 + 3 + 5 + 7 = 17, and 17 ÷ 4 = 4.25, the mean. The median is the middle number, or, if the list contains an even number of elements, the average of the middle two elements (when they are arranged
in increasing order). In this case, the average of 3 and 5 is 4. Quantity A is greater than Quantity B.
4. D Use the given averages to figure out Susan’s total distance: 4 hours at an average speed of 50 miles per hour is a total of 200 miles, and 2 hours at an average speed of 20 miles per hour is a total of 40 miles. Susan goes a total of 240 miles in 6 hours, thus, her average speed is 
, or 40 miles per hour. The answer is choice (D).
5. B To calculate the probability, divide the part by the whole: 
. Choice (B) is correct because 
(which is simply 
multiplied by 2).
6. A Although you can’t find an exact value for either quantity, you can find a possible range for each. In Quantity A, if all 4 numbers are between 5 and 6, then their average is, too. Similarly, in Quantity B, if all 6 numbers are between 4 and 5, then so is their median. Any number between 5 and 6 is
greater than any number between 4 and 5, so Quantity A is greater.
7. A Remember that mode means the number that appears “most often.” Plug In the Answers. For choice (C), if x = 4, then the numbers become: 8, 9, 10, 13, 16. For a list of numbers to have a mode, there has to be at least two of one of the numbers. So this list has no mode; eliminate
choice (C). For choice (A), if x = 2, then the numbers become: 4, 7, 4, 3, 8. Because 4 appears twice, 4 is the mode—the answer is choice (A).
8. B Think of this problem as if you’re pulling out an even ticket and then another even ticket. So, for the first ticket there are 9 possible evens out of 18 total, so the probability that the first ticket is even is 
. Now you have one fewer even ticket in the hat. So there are 8 evens out of 17 total tickets for the second ticket, thus, the probability is 
. You want an even AND an even, so multiply: 
. The answer is choice (B).
9. A Plug in numbers and use the rate formula—amount = rate × time—to check the quantities. If j = 1 and k = 2, then Quantity A is 2 minutes and Quantity B is 
minutes. Quantity A is greater, so eliminate choices (B) and (C). Any acceptable set of values gives the same outcome; select choice (A).
10. B This is the number of combinations of 8 items taken 5 at a time (because the order does not matter). This number is equal to 
.
11. A Adding the standard deviation (20) to the mean (60) gives you the number of passengers in a car that carries exactly one standard deviation above the mean number of passengers (80). The first standard deviation above the mean represents 34% of the population in a normal distribution, and a further 50% falls below the
mean, so 84% of the cars will carry 80 people or fewer. Subtracting this from the entire population (100%) gives you the percent of cars that carry greater than 80: 100% − 84% = 16%. The answer is choice (A).
12. C To find the average, divide the total by the number of values. So, 
> 25. Multiply both sides of the inequality by 4 and then subtract 22 (10 + 12) to find 2n > 78. Divide by 2 to find n > 39. So,
n is NOT 39; it is the least integer greater than 39, which is 40. Alternatively, you could plug in the answers starting with choice (A) because the question asks for the least possible value. If n = 38 or 39, then the average is not greater than 25. If n = 40, the average is greater than 25. The answer is choice (C).
Drill 2
1. C In Quantity A, if y = 4, then the numbers (arranged in increasing order) become x, x2, x3, x4, x4, x6; the mode is
x4. In Quantity B, if y = 5, then the numbers become x, x2, x4, x4, x5, x6. Usually, you’d need to take the average of the middle two numbers to find the median because there is an even number of values, but in this case they’re both x4. The median, then, is x4, so the quantities are equal. Because x > 1, you don’t have to worry about special cases such as 0, 1, negatives, or fractions, and the correct answer is choice (C).
2. B Rate is calculated by dividing the distance traveled by the time elapsed. Plug In to compare the two rates. If you plug in x
= 4 and y = 2, the rate for trip A will be: 
mph and the rate for trip B will be: 
mph; eliminate choices (A) and (C). Any set of values will have a greater rate for trip B, so select choice (B).
3. A Plug In to make this problem much simpler. If you plug in x = 2, then the probability for the second event is: 
. Now, because this is an “and” probability problem, you multiply the two probabilities
together to find the target answer: 
. Choice (A) is the only one that works: 
.
4. 19 Take the problem a piece at a time. If a set has only two numbers, the median is the average of those two numbers. Set up average wheels for each of the first two averages. For the first one, two numbers that average 13 total to 26. For the second average, three numbers that average 23, so the must have a
total of 69. Set up one final average wheel for all five numbers: 5 numbers total 95. Solve for the average, and you should get 19 from 95 ÷ 5.
5. B Quantity A asks for the probability “without replacement,” so that means you have to take into account that there will be one marble less in the total after each draw. The probability of first choosing a red marble is 
, a second red marble is 
, and then a green marble is 
. This is an “and” probability problem, so you have to multiply the probability of each event together: 
. For Quantity B, you do the same thing, but the total stays the
same for each draw: 
. Quantity B is greater.
6. 64 To find the least possible value of p, work with the lowest possible average, 29. Draw an Average Pie. You have 3 values with an average of 29, so your total is 3 × 29 = 87. Now you know that 31 + 41 + p = 87, so p = 15, and (p — 7)2 = 64.
7. A Remember that amount = rate × time. So, 25 liters = rate × 40 minutes. The rate was 
liters/min. The net rate at which the bucket is filling is the difference between the
hose’s rate and the leaking rate. So, (1 liter/min) – (leaking rate) = 
. Solve for the leaking rate to find the leaking rate is 
liters/min; the answer is choice (A).
8. A There are a total of 62 = 36 possibilities for each toss. There are a total of 8 ways we can get a total of 7 or 11 on the first toss: 6 ways to get a total of 7—(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), or (6, 1)—plus 2 ways to get a
total of 11—(5, 6) or (6, 5). Therefore, the probability of getting a total of either 7 or 11 on the first toss is 
. The probability of getting a total of 7 on the second toss is 
so the probability that both of these independent events occur is the product 
, choice (A).
9. D Try plugging in a number for s that divides easily by 60, such as 7,200. So, if s = 7,200 seconds, that’s 120 minutes or 2 hours. Plug in a nice number for r such as 5. So, if the copier makes 5 pages per hour for 2 hours, your target is 10 pages. Plug s =
7,200 and r = 5 into the answers. Ballpark: Choice (A) is too large, choice (B) too small, choice (C) too small, and choice (E) far too large. Only choice (D) yields your target of 10.
10. C Plug in a value for p. Try p = 16: In Quantity A, then 16 hinges cost a total of 32 cents, for an average cost of 2 cents per hinge; in Quantity B, 4 hinges cost a total of 8 cents, for, again, an average cost of 2 cents per hinge. The quantities are equal, so eliminate choices (A) and (B). Any value
for p will yield the same results: The quantities will always equal; the answer is choice (C).
11. 2 Draw two bell curves: one for rural areas, and one for urban areas. The three standard deviations above the mean each represent 34%, 14% and 2% of the population, respectively. The mean in both cases is 8. In rural areas, 2% of the citizens take more than 12 holidays a year, so 12 is two standard deviations above 8; the
standard deviation is thus the difference between 8 and 12 divided by 2, or 2. In urban areas, similarly, the standard deviation is 16 – 8 divided by 2, or 4. The difference between the two standard deviations is thus 4 – 2 = 2.
12. A There are a total of 63 = 216 total possible rolls for the three dice. First figure out the probability of getting exactly two 1’s. There are 5 × 3 = 15 ways this could happen: 112, 113, 114, 115, 116; 121, 131, 141, 151, 161; or 211, 311, 411, 511, 611. You could repeat this
list of 15 possibilities in the obvious way for exactly two 2’s, exactly two 3’s, and so on. Thus, the total number of favorable rolls is 6 × 15 = 90. Because there are 216 possible rolls, 90 of which are favorable, the probability of getting exactly two of the three dice to show the same number is 
, choice (A).
Drill 3
1. B If the class average is 82% on a 50-point test, the average score was 41 points out of 50. Use the Average Pie to find the sum of the class’s scores: (41)(32) = 1,312. To reach a class average of 86%, each student will need to average 43 points out of 50 points. Use the Average Pie to find the
desired sum of the class’s scores: (43)(32) = 1,376. The difference is 1,376 − 1,312 = 64, so the class needs to make up 64 points; 
=16, so 16 students need to answer the extra credit question correctly. The answer is (B). Alternatively, notice that the class’s average needs to increase by 4%, or 2 points on average for a 50-question test. But the extra credit is worth 4 points, so
to average half of a 4-point increase, only half the students (16) need to get the extra credit correct.
2. D Before Phil leaves, Vinay has traveled for 4 hours; the rate formula is distance = rate × time, so Vinay has gone 40 miles per hour × 4 hours = 160 miles. Upon leaving, Phil is gaining on Vinay at a rate of 10 miles per hour, because he travels 10 more miles per hour than
Vinay. Now your equation is 160 miles = 10 miles per hour × time, so time = 16 hours. Phil left at 5 a.m., so he’ll catch up to Vinay at 9 p.m., so the answer is choice (D).
3. B Since there are variables in the answer choices, try plugging in 2 for x. Your two middle numbers are now 7 and 9, and the median is their average, 8. Circle 8 as your target answer. After you check all the choices, only choice (B) matches.
4. 
First, figure out how many different results that Damon can get: Each die has 6 sides, so the total number of possible outcomes is 6 × 6 × 6 = 216. Now count out how
many of those outcomes total more than 16. There are 3 ways to roll a 17—5, 6, and 6, 6, 5, and 6, and 6, 6, and 5—and 1 way to roll an 18—three 6’s. The probability is thus 
, which reduces to 
.
5. B and D
If you pare down the problem, then it is much simpler than it first appears. There will be 1 house on Surf Street at which a turtle will lay its eggs; this is “the number of outcomes you want.” There are a total of 5 houses, which is the
“total number of possible outcomes.” Therefore, if John spends the summer on Surf Street, the probability of John staying in the house where the sea turtle will lay its eggs is choice (B), 
, and the information about the landside houses versus seaside houses actually turns out to be unnecessary. Similarly, if John stays on Breaker Way, there will be 1 house that a turtle will lay its
eggs at out of a total of 3 possible houses that John could live in. Therefore, if he lives on Breaker Way, there is a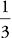 
chance that the turtle lays its eggs outsides John’s house, and this makes choice (D) correct.
6. 
The most efficient way to approach this tough problem is to plug in prime numbers to determine the set of values that satisfies the inequality. Plugging 2 in for x yields 
which is true. Plugging in 3 yields 
which is also true. Plugging in 5 yields 
so the two sides are equal, so that’s probably the maximum value of x. To be sure, check the next prime number, 7:
which is false. You should also check a large prime number to confirm {2, 3, 5} is the solution set. If you do, you’ll find the inequality is false and {2, 3, 5} is the full set of values. To find the average of the numbers, use the Average Pie: 
7. C There are variables in the answer choices, so Plug In. Try x = 3. Now write out your new set of numbers. Since you are subtracting 3 and adding 3 the same number of times, the sum and average stay the same, so eliminate choices (A) and (B). The median decreases by 0.5, so eliminate choices
(F) and (G). There are now two modes in the set, so eliminate choice (D). The distance of the numbers from the mean changes in the new set, so the standard deviation is not the same. Eliminate choice (E). The correct answer is choice (C).
8. 7.6 Alejandra’s average equals 227 ÷ 5 = 45.4. Nigel’s average equals 189 ÷ 5 = 37.8. The difference is 7.6.
9. B First place the known values from the question in order: 56, 86, 97, 98. From the restriction, you know that x can only be placed in two slots: first (before 56) and second (between 56 and 86). In both cases, the middle number of the full set is 86, making choice (B) the only correct choice.
10. 
First figure out how many marbles of each color are in the jar. For blue: of 40 is 8, so there are 8 blue marbles and 32 other marbles. For red: 
of 32 is 8, so there are 8 red marbles and 24 marbles that are neither red nor blue. As there are 10 green marbles, there are 14 marbles left that are not green, red, or blue. Thus, the probability of selecting one of those marbles is 
. If you answered 
, you
found the probability that the selected marble will be blue, red, or green. If you answered 
, for the red marbles you perhaps found of 40 (the total marbles) rather than of 32 (the remaining marbles after blue) in the original
calculation.
11. D Set up your standard bell curve with the proper percentage markers of 2%, 16%, 34% on each side of the central average line. Use an average wheel to find the average sales amount in dollars; you should get 91,000 ÷ 65 = 1400 as the average. Note that at the 50% mark, and then note the amounts
at each deviation above and below the average by adding or subtracting the given standard deviation of $130. Once you’ve filled in the curve, look for $1270 from the question. It is at the 16% mark, indicating that less than 16% of employees sold under $1270 worth of merchandise. Therefore, the other 84% of employees were able to sell $1270 or more worth of merchandise, making choice (D) the correct answer.
12. 93 Use the Average Pie. Consider Cliff and Raya’s average first: There are 2 of them, and their average is 79, so multiply 2 × 79 to get their total of 158. Call Cliff’s score c, and c + 73 = 158, so c = 85. Now repeat the process with Jamal and Cliff’s average: 2
people with an average of 89, so 2 × 89 = 178 total points. Therefore, x + 85 = 178, and x is 93.
Drill 4
1. A, C, and D
Draw a bell curve with three standard deviations to the left and the right of mean. Plug in 50 lbs on the leftmost standard deviation as mentioned in the question. Start with choice (A), plug in 80 lbs for the mean, and solve for the standard deviation. In
this case it would be 10, and it’s possible to see that 110 would be the third standard deviation to the right of the mean. Therefore, choice (A) satisfies the question. If you repeat this with choice (B), you’ll find that the standard deviation would have to be 11.67. Thus, the value two standard deviations to the right of the mean is 108, and is just shy of what you want. In choice (C), the mean is 86, the standard deviation is 12, and 110 will be the second
deviation to the right of the mean. Choice (D) works; the mean is 95, standard deviation is 15, and 120 is the first value to the right of the mean. You can Ballpark to eliminate choice (E). Its standard deviation is about 16, and the first standard deviation to the right would be about 116, which means 110 cannot fall on a standard deviation.
2. B Use the Rate Pie. Ali is traveling 50 feet per second faster than Jeff is traveling. Therefore, that is the rate at which she is effectively gaining ground on him. Put that in the lower-right segment of the Rate Pie. We want to know how long it will take her to gain 3,000 feet on him. Put 3,000 in the
top section of the Rate Pie. Now you can see that dividing 
will fill in the last segment of the Rate Pie, telling you how long it takes Ali to do so is 60 seconds. Be aware that choice (E) is an incorrect partial answer. Now you need to find out how many feet Ali will travel in 60 seconds, by multiplying 60 second × 300 feet per second, which equals 18,000 feet. Divide 18,000 feet by the length
of one lap, or 3,000 feet, and you’ll find that it will take Ali 6 laps to overtake Jeff.
3. 
or 0.3
You don’t know how many trees there are, so define the job by plugging in an easy number, such as 21 trees. Use rate pies to figure out that Helen’s rate is 7 trees/hr and Sergey’s rate is 3 trees/hr. That means their combined rate is 10 trees/hr. Put their combined rate into another rate pie with the total trees to find it takes them 
or 2.1 hours to meet. To find out how many trees Sergey has cut down at this point, put his individual rate into another rate pie with 2.1 hours. 3 trees/hr × 2.1 hours = 6.3 trees at the point they meet. Put the number of trees Sergey has cut when they meet over the total trees: 
, so the correct answer is 
or
0.3.
4. E Start by plugging in a set of consecutive integers that encompasses the full spectrum of integers, such as −2, −1, 0, 1, 2. The average and median of the set are both 0. In any set of consecutive integers, the average will always equal the median. Performing the operations in choices (A),
(B), (C), and (F) results in sets of numbers that are still consecutive. Thus, while in choices (B), (C), and (F) the averages change, the medians also change to those same values. Eliminate choices (B), (C), and (F). In choice (A), neither the average nor the median changes, so you can eliminate it as well. For choice (D), the new average is −1.64 and the new median is −8.2. Again, both values change, so you can eliminate choice (D). In choice (E), the new average
is .4, but the median hasn’t changed; choice (E) works. You can eliminate choice (G) based on the other calculations, and the only correct answer is choice (E).
5. E and G
Plug in numbers for p, s, and h, such as 2, 3, and 4, respectively. If Paul can grade 2 essays every half hour, then in 4 hours, he will grade 16 essays. If Sarah can grade 3 essays every hour, then in 4 hours, she will grade
12 essays. Thus, Paul and Sarah will grade a total of 28 essays. Now, plug your numbers into each answer choice. Choices (E) and (G) result in 28. If you Plugged In and choice (F) also worked, you picked the same number for Paul and Sarah. If you picked choice (C), you didn’t notice that Paul grades p essays every half hour, not every hour.
6. E Use the Average Pie to solve each part of the problem. If the average of 5 numbers is 36, then the sum of those numbers is 180. If the average of four of the numbers is 34, then the sum of those numbers is 136.
7. 17 Use the Rate Pie to organize your work. For the first 5 weeks, Noah’s company builds 1 mile per week. Therefore, they build 5 miles of road before the start of the rainy season. Once rainy season begins, they have 6 miles of road left to build. This number is
the “work,” and goes in the top of the rate pie. The rate, 
miles per week, goes in the lower left segment of the rate pie. Divide 6 by , and you’ll get the total amount of time, or 12 weeks, at that rate. Therefore, it will take a total of 17 weeks for Noah’s company to build the road.
8. A, D, and F
Plug in for y. If y = 30, then Employee A produces 30 DVDs in 
of an hour, so using a Rate Pie you can figure out that his rate is 75 DVDs per hour.
Employee B produces 30 DVDs in 
of an hour, so his rate is 50 DVDs per hour. Employee C produces 30 DVDs in 
of an hour, so his rate is 24 DVDs per hour. 5y = 150, so you need to find the combination of employees that can produce 150 DVDs in 2 hours. Employee A will produce exactly 150 DVDs in 2 hours, so choice
(A) is a credited answer. If you know that Employee A alone can produce 5y DVDs in 2 hours, then choices (D) and (F) must also be correct answers, and choice (G) must be incorrect. Employee B will only produce 100 DVDs in 2 hours, so you can eliminate choice (B). Employee C will only produce 48 DVDs in 2 hours, so you can also eliminate choice (C). If Employees B and C work together for 2 hours, they will produce 148 DVDs, so choice (E) is incorrect.
9. 25 Cyclist A rode for 3.5 hours at 20 miles per hour, so she traveled 20 × 3.5 = 70 miles. Cyclist B then, must have traveled 145 – 70 = 75 miles. Since Cyclist B left at 2:00, she rode for 3 hours, giving her a speed of 75 ÷ 3 = 25 miles
per hour.
10. D The question is asking for a specific amount and there are no variables in the answers, so PITA. Starting with choice (C), if the probability of her getting a dude is , then the probability of her getting a dud is 
. Thus, the probability of her getting two consecutive duds is 
=
, which is too big. Eliminate choice (C). To get a smaller chance of getting two duds, you need a larger chance of getting a dude; eliminate choices (A) and (B). In choice (D), the probability of her
getting a dude is , which means the probability of her getting a dud is 
. Thus, the probability of her getting two consecutive duds is 
, which matches the probability mentioned in the question. The correct answer is choice (D).
11. 1.28 First, find the two people’s rates in terms of miles per hour (mph). Victor’s rate equals distance over time, or 1 mile over 
hours, which equals approximately 3.529 mph. Calculating Sarah’s speed using the same steps gives
you her rate, 4.286 mph. When added, the two rates become their combined rate of 7.815 mph. When you divide 10 miles by 7.815, the answer is approximately 1.28 hours until they meet.