ANSWERS

Drill 1

  1.      A

  2.      C

  3.      C

  4.      B

  5.      468,000

  6.      D

  7.      D

  8.      D

  9.      D

10.      60

11.      B

12.      A

13.      A, B, D

14.      C, D

Drill 2

  1.      D

  2.      A, E, F

  3.      504

  4.      840

  5.      C

  6.      660

  7.      C, E

  8.      E

  9.      A, B

10.      1320

11.      A, B, D

12.      B

13.      A, B, C, E, F, G

14.      56

EXPLANATIONS

Drill 1

  1.  A  For Quantity A, there are 8 options for president and 8 options for vice president, giving you 8 × 8 = 64 total assignments. For Quantity B, once you pick a woman to be president, there are only 7 women left to be vice president, giving you 8 × 7 = 56 assignments. The answer is choice (A).

  2.  C  When you see the word approximately, you are being told to Ballpark. In this case, you have 26 possibile letters for that slot, 5 for the second slot, and 21 for the third slot. Estimate and call this 25 × 20 × 5. The total is 2,500, so select choice (C).

  3.  C  Substitute the given values into the groups equation: Total = Group 1 + Group 2 − Both + Neither. 100 = 60 + 40 − 30 + N, giving you N = 30, choice (C).

  4.  B  Quantity A places a restriction on which meals a chef can cook because each chef must cook a distinct meal. In this case, there would be 3 × 2 × 1 = 6 different assignments. Quantity B does not place a restriction on which meals a chef can cook. In this case, there would be 3 × 3 × 3 = 27 different assignments, choice (B).

  5.      468,000
List the number of possible options for each character in the password. There are 10 possibilities for the first digit, 9 left for the second, and 8 left for the third. There are 26 possibilities for the first letter and 25 for the second. There are 10 × 9 × 8 × 26 × 25 = 468,000 possible passwords.

  6.  D  Substitute the given values into the groups equation: Total = Group 1 + Group 2 − Both + Neither. So 190 = 95 + 75 – 12 + N. N = 32. If you pick a number larger than 12 to represent the number of students who buy both cookies, the number that buy neither cookie also increases. The question asks for the least number that bought neither cookie, so the answer is choice (D).

  7.  D  First find the number of groups of fish he can select. This is your number of slots: _ _ _ _ _. There are six fish he can choose for the first slot, 5 for the second and so on: 6 5 4 3. Since order doesn’t matter, you need to divide by the factorial of the number of slots: . Reduce your number to get 3 × 5 = 15. For plants you have two slots so = 3. 3 × 15 = 45. The answer is choice (D).

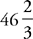  8.  D  Dividing 100,000 seconds by 3,600 seconds per hour, you get 27 hours plus hr. Multiplying hr by 60 minutes per hour, you get minutes. Therefore, to the nearest minute, 100,000 seconds is equal to 27 hours, 47 minutes. After 24 hours, the time will be 9:30 p.m. Wednesday; 3 hours, 47 minutes after that, it will be 1:17 a.m., Thursday, choice (D).

  9.  D  To find the number of different committees. Make your slots and divide by the factoral =84; eliminate choice (B). To find the number of ways to arrange the committee members, just multiply 9 × 8 × 7 = 504, and eliminate partial choice (E). The difference is 504 − 84 = 420, choice (D).

10.  60  When calculating the number of games, order does not matter. There are two students in each game, so two slots: 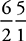, because order does not matter you will divide by the factoral for 15 combinations. Each student plays 4 games against each of the other students, so 4(15) = 60 games are played.

11.  B  Start by finding out how many groups of three seniors can be chosen from the five seniors: =10. Next, multiply that total by the number of individual juniors with which those groups can be paired (7) to form the full committee: 10 × 7 = 70. Quantity B is greater.

12.  A  You are forming groups where order doesn’t matter, so use the combination formula. If you use 5 ingredients, then there are: 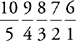=252 different combinations. If you use 6 ingredients there are 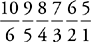=210 combinations, if you use 7 there are =120, and if you use 8 there are =45. Thus, Quantity A is 8, and Quantity B is 5, choice (A).

13.       A, B, and D
This problem is about combinations, because order doesn’t matter. On a night when the pizza place offers only seven toppings, Sam has (7 × 6 × 5) ÷ (1 × 2 × 3) = 35 options, choice (A). When the pizza place has eight toppings, Sam has (8 × 7 × 6) ÷ (1 × 2 × 3) = 42 options, choice (B). And when the pizza place has nine toppings, Sam has (9 × 8 × 7) ÷ (1 × 2 × 3) = 84 options, choice (D).

14.      C and D
Simplify this problem by dealing with the two combinations separately. To select 2 out of 7, 8, or 9 ice creams, calculate , and to yield 21, 28, or 36 possible combinations of ice creams, respectively. Now, so the same thing for sauces: 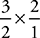= 3, and = 6, so you have 3 or 6 possible combinations of sauces. The possible numbers of different Deluxe Sundaes, then, are 21 × 3 = 63; 21 × 6 = 126; 28 × 3 = 84; 28 × 6 = 168; 36 × 3 = 108; and 36 × 6 = 216. Only choices (C) and (D) work.

Drill 2

  1.  D  This is a permutation because order matters. First, think about the positions for the 2 governors from Alaska and Hawaii. There are 5 pairs of spots they can occupy: first and second, second and third, third and fourth, fourth and fifth, or fifth and sixth. That gives you 5 possibilities; since either governor could come first, you have a total of 5 × 2 = 10 possible ways to arrange those 2 governors. Meanwhile, for each of those options, the other governors can assume any of the remaining spots, which equals 4 × 3 × 2 × 1, or 24 possibilities. The answer is thus 10 × 24 = 240, choice (D).

  2.      A, E, and F
If Jeff watches one movie, he has four different choices for that one movie, so choice (A) is a correct answer. To find the total number of arrangements of two movies, first write out two slots. For the first movie, he has 4 choices and a 4 goes in the first slot. For the second movie, he now has three choices and a 3 goes in the second slot. 4 × 3 = 12, so choice (E) is correct. There are 24 arrangements if he watches three movies: 4 × 3 × 2 = 24. Choice (E) is also correct.

  3.  504 This problem deals with permutations because the order of the statues matters. Draw three slots for the three positions. You can choose from nine statues for the first spot, eight for the second, and seven for the third. Multiplying these values together gives you 504.

  4.  840 There are 10 possible presidents. After the president is selected, there are 9 members left to fill the remaining 3 spots. Order does not matter, so the number of possibilities for the other three spots is . Simplifying the fraction yields 3 × 4 × 7 = 84. So, there are 10 possible presidents and 84 possible committees for each president. Multiplying them yields the total number of possible committees, 840.

  5.  C  This problem is about combinations, because the order of the dishes does not matter. Since you’re choosing 4 dishes, start by drawing 4 blanks. On top, write the number of choices: 12 choices for the first dish, then 11, 10, and 9. On the bottom, start with the size of the smaller group and count down: 4, 3, 2, and 1. Cancel the numbers on the bottom, and the numbers on top will multiply to 495.

  6.  660  The order of entrees the guests chose from does not matter. Therefore, the number of different possibilities of entrees is 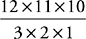=220. The order of desserts does not matter either, so there are 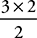=3 possible different combinations of desserts. Multiplying the two together gives a total of 660 possible different combinations of offerings.

  7.      C and E
This problem is about permutations, because the order of the figurines matter since they each look unique. You have two cases to consider here. Start with the option that Margaret buys three witches and three ghosts. In that case, she has 3 choices of witch for the first spot, 3 choices of ghost for the second spot, 2 choices of witch for the third spot, 2 choices of ghost for the fourth spot, 1 choice of witch for the fifth spot, and 1 choice of ghost for the sixth spot: Hence, her total number of arrangements is 3 × 3 × 2 × 2 × 1 × 1 = 36, which is choice (C). If she buys four of each figurine, her number of arrangements is 4 × 4 × 3 × 3 × 2 × 2 × 1 × 1 = 576, choice (E).

  8.  E  The order of cars matters, so you simply need to multiply the number of possible cars for each spot. For the first car, there are six possible, for the second, five, and so on. So your scratch paper should look like this: 6 5 4 3 2 1, which is equivalent to 6!, or 720.

  9.  A, B  The order of friends doesn’t matter. There are five friends to choose from for three spots, so the top of your fraction should read: 5 4 3, and to correct for the order of friends not mattering, the bottom of your fraction should be: 3 2 1. 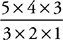= 10. Since he is numbering possibilities sequentially, the numbers 1 through 10 will be on the list, making choices (A) and (B) correct.

10.  1,320  In this case, order matters, so you simply need to multiply the number of possible runners for each spot. That should look like this: 12 11 10 = 1,320.

11.       A, B, and D
Starting with choice (A), there are 3 slots on the team, with 5 experienced engineers available for the first slot, 4 for the second slot, and 3 for the third slot. Order doesn’t matter, so divide by 3! to get = 10. Choice (A) is correct. For choice (B), you have 3 apprentice engineers available for 2 slots and once again, order doesn’t matter. = 3. Choice (B) is correct and you can eliminate choice (C), which contradicts choice (B). For choice (D) you have = 10, so choice (D) is correct. Choice (E) is incorrect because 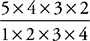= 5. The correct answers are choices (A), (B), and (D).

12.  B  This is a permutation problem, so lay out your slots to fill and then multiply. For choice (A) you have 1 slot for a letter and two slots for digits. There are 26 choices for your letter and 10 choices for your first digit. Because you can’t repeat digits, there are 9 choices for your second digit. Thus, the number of different codes that can be made is 26 × 10 × 9 = 2,340. Eliminate choice (A). For correct choice (B), you have two spots for letters and two for digits, so you have 26 × 26 (letters can repeat) × 10 × 9 = 60,840. Choice (C) is incorrect because the number of different codes consisting of one letter and one digit is 26 × 10 = 260. The only correct answer is choice (B).

13.     A, B, C, E, F,and G
Rather than writing out every possible outcome, see if you can express the answer choices as the product of 3 factors that could be the number of ties, shirts, and jackets Brian receives. Choice (A) is possible: 3 ties × 2 shirts × 1 jacket = 6 outfits. Choice (B) is possible: 4 ties × 2 shirts × 1 jacket = 8 outfits. Choice (C) is possible: 3 ties × 3 shirts × 1 jacket = 9 outfits. Choice (D) is not possible: you’d need a 5 as a factor to get to 10, and Brian can’t receive 5 of anything, so eliminate choice (D). Choice (E) is possible in 2 different ways: 3 ties × 2 shirts × 2 jackets = 12 outfits, as does 4 ties × 3 shirts × 1 jacket. Choice (F) is possible: 4 ties × 2 shirts × 2 jackets = 16 outfits. And, finally, choice (G) is possible: 3 ties × 3 shirts × 2 jackets = 18 outfits. All of the choices except choice (D) work.

14.  56  This problem involves permutations, because the order matters since the ties are all distinct. Start with Paul wearing a red tie. He has 3 red tie choices and Allen has 2 remaining red tie choices, giving them a product of 6 permutations. For green ties, they have 5 × 4 = 20 permutations. For blue ties, they have 6 × 5 = 30 permutations. The grand total is 56 permutations.