Un rectángulo
de cuadrados

Marta Macho Stadler

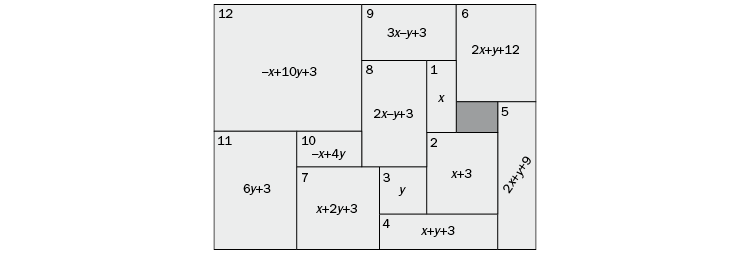
Tenemos un rectángulo R que está subdividido en trece cuadrados como muestra la figura:

¿Cuadrados? Bueno, algún cuadrado sí que hay... pero desde luego, no todas las figuras que forman R lo son. Es verdad, no te preocupes, ni te falla la vista ni me he equivocado. Ahora te lo explico.

Para que el problema planteado no sea de resolución trivial, los cuadrados que forman el rectángulo R se han deformado ligeramente, y en su mayoría ya no lo parecen. Es decir, la figura mostrada está levemente distorsionada, aunque sabemos que las alineaciones de los cuadrados que forman originalmente R son las mismas que las de los rectángulos de la imagen. Sabemos también que el cuadrado negro mide 3 cm de lado.

El desafío consiste en calcular las medidas de los lados de cada uno de los doce cuadrados restantes y del rectángulo R.

Espero que ahora entiendas la razón por la que se ha distorsionado la figura: en otro caso, podrías haber tomado una regla, y haber solucionado el problema haciendo unas pocas medidas y un par de sumas.

Solución

Partiendo del cuadrado negro se trata de ir calculando las medidas de los cuadrados que forman el rectángulo R paso a paso, deduciendo la longitud de cada lado a partir de las longitudes obtenidas anteriormente. Hemos numerado los cuadrados para indicar el orden en el que vamos a ir realizando los cálculos.

Comenzamos el proceso, indicando en la imagen de debajo los resultados obtenidos:

1. Suponemos que el lado del cuadrado 1 mide x.

2. Así, el lado del cuadrado 2 mide x + 3 (al ser el cuadrado negro de lado 3).

3. Suponemos que el lado del cuadrado 3 mide y.

4. Entonces, el lado del cuadrado 4 mide x + y + 3 (suma de las longitudes de los lados de los cuadrados 2 y 3).

5. Por lo tanto, el lado del cuadrado 5 mide 2x + y + 9 (suma de los lados de los cuadrados negro, 2 y 4).

6. De aquí se deduce que el lado del cuadrado 6 mide 2x + y + 12 (suma de los lados de los cuadrados negro y 5).

7. Razonando del mismo modo, el lado del cuadrado 7 mide x + 2y + 3 (suma de las longitudes de los lados de los cuadrados 3 y 4).

8. Así, el lado del cuadrado 8 mide 2x − y + 3 (ya que la suma de las longitudes de los lados de los cuadrados 1 y 2 coincide con la suma de los lados de los cuadrados 3 y 8).

9. Es claro, por tanto, que el lado del cuadrado 9 mide 3x − y + 3 (suma de los lados de los cuadrados 1 y 8).

10. Entonces, el lado del cuadrado 10 mide −x + 4y (ya que la suma de los lados de los cuadrados 8 y 10 coincide con la suma de las longitudes de los lados de los cuadrados 3 y 7).

11. De aquí es inmediato que el lado del cuadrado 11 mide 6y + 3 (suma de los lados de los cuadrados 7 y 10).

12. Y, por último, el lado del cuadrado 12 mide −x + 10y + 3 (suma de los lados de los cuadrados 10 y 11).

Para terminar, basta con encontrar los valores de x y de y. Una manera de hacerlo, consiste en comparar cuadrados de zonas que no han sido relacionadas durante la construcción, por ejemplo:

1. La suma de las longitudes de los lados de los cuadrados 1 y 9 coincide con la suma de las longitudes de los lados del cuadrado negro y del 6, es decir:

x + (3x − y + 3) = 3 + (2x + y + 12),

y despejando se deduce que x = y + 6.

2. La suma de las longitudes de los lados de los cuadrados 10 y 12 coincide con la suma de las longitudes de los lados de los cuadrados 8 y 9, es decir:

(−x + 4y) + (−x + 10y + 3) = (2x − y + 3) + (3x −y + 3),

y despejando se deduce que 16 y = 7x + 3.

Tenemos un sistema de dos ecuaciones con dos incógnitas:

x = y + 6
16y = 7x + 3

de solución x = 11 e y = 5.

Así, las medidas de cada cuadrado quedan como indica la figura que sigue (ya con sus proporciones reales), y el rectángulo mide 112 cm (suma de los lados de los cuadrados 11 y 12) por 75 cm (suma de los lados de los cuadrados 11, 7, 4 y 5 o 12, 9 y 6).

MÁS INFORMACIÓN

Este problema estaba planteado en la revista francesa Tangente (http://tangente.poleditions.com) 99 (julio 2004).

En la página web http://www.squaring.net/ puede encontrarse información exhaustiva sobre este tipo de problemas que consisten en dividir rectángulos en cuadrados. Estos Squared Rectangles deben obtenerse utilizando cuadrados de diferentes tamaños, buscando el mínimo número de cuadrados para realizarlo, etc. ¡No es nada sencillo!