Dos alfombras triangulares

Inmaculada Fernández Benito

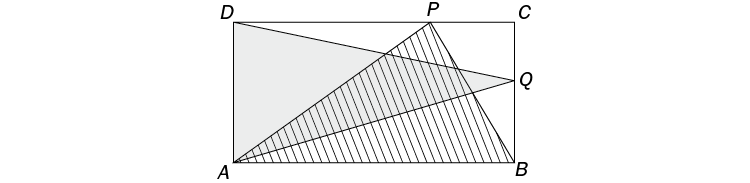
En una habitación de planta rectangular, ABCD, se colocan dos alfombras triangulares: una de ellas, ABP, es rayada y la otra, DAQ, gris, como en la figura.

Se sabe que el área de la parte no cubierta por las alfombras (sin sombrear en la figura) mide 4,2 m2. ¿Cuánto mide el área del cuadrilátero determinado por la región en la que se superponen las dos alfombras?

Solución

Observamos que el triángulo ABP se divide, al trazar su altura, en dos triángulos rectángulos, ARP y BRP; también vemos que el rectángulo ABCD contiene, además de estos dos triángulos, otros dos, ADP y BCP, congruentes respectivamente con los dos anteriores. De aquí se deduce que el área del rectángulo ABCD es doble de la del triángulo ABP. Razonando análogamente para la alfombra DAQ, se obtiene que su área es la mitad de la del rectángulo y, por tanto, la misma que la de la alfombra ABP.

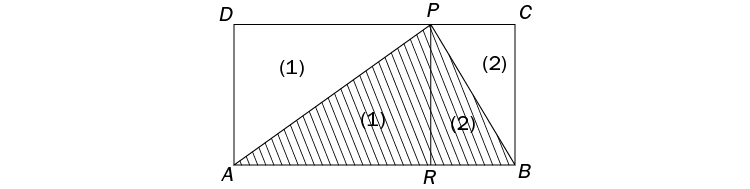
De ello se concluye que la suma de las áreas de las dos alfombras es igual al área del rectángulo y, en consecuencia, que el área de la zona no tapada debe ser igual a la de la zona de superposición de las alfombras, es decir, el área del cuadrilátero formado al superponerse las alfombras es 4,2 m2.

A la conclusión (clave para resolver el problema) de que el área total del rectángulo es la suma de las áreas de las dos alfombras, también se puede llegar aplicando las fórmulas del área de un rectángulo AR = base ⋅ altura y de un triángulo 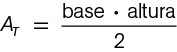, teniendo en cuenta asimismo que la base del triángulo ABP es la altura del DAQ y, recíprocamente, que la altura del ABP es la base del DAQ.

MÁS INFORMACIÓN

El enunciado de este problema es una variante de una pregunta de respuesta múltiple propuesta en el Concurso Canguro Matemático para segundo de Bachillerato del año 2006 y enunciada en los siguientes términos:

Los puntos M y N se eligen en los lados AB y BC del rectángulo ABCD de la figura. Luego el rectángulo se divide en varias partes, tal como se indica.

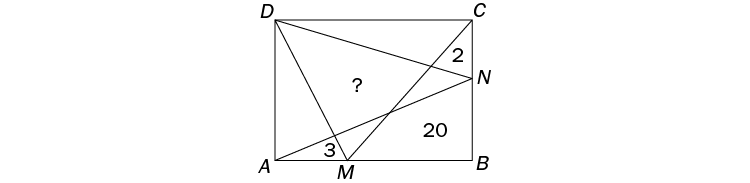
Se conocen las áreas de tres de esas partes, marcadas en la figura igualmente. Hallar el área del cuadrilátero marcado con “?”.

Marca la respuesta correcta:

A) 20 B) 21 C) 25 D) 26 E) Faltan datos

Fue el profesor Francisco Bellot, Presidente de la Asociación Canguro Matemático Europeo, quien me habló de este problema, cuya belleza y simplicidad de resolución, aplicando el Teorema de las alfombras, me sedujeron desde el primer momento.