Doce vértices, ¿y seis distancias distintas?
Irene Ferrando Palomares y Alejandro Miralles Montolío
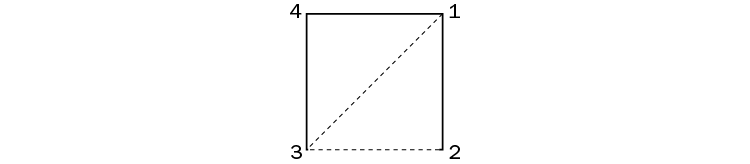
En un cuadrado es muy fácil observar que no podemos emparejar sus cuatro vértices, sin repetir ninguno, de forma que obtengamos dos segmentos de longitud distinta. O bien podemos conseguir las dos diagonales o bien dos de los lados pero nunca podremos obtener un lado y una diagonal emparejando vértices distintos.
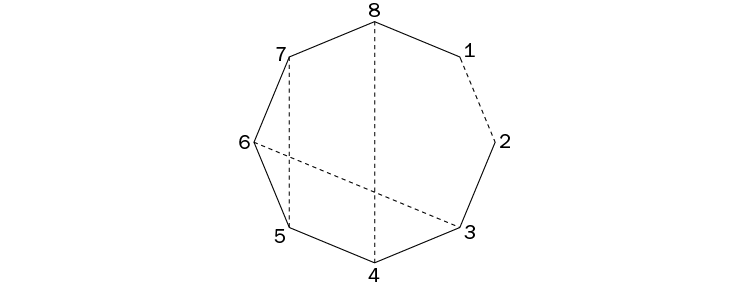
En cambio, en un octógono regular, sí que podemos emparejar sus ocho vértices, sin repetir ninguno, para obtener cuatro segmentos de distinta longitud. Numerando los vértices del octógono del 1 al 8 en el sentido de las agujas del reloj, una forma de emparejarlos sería: (1, 2), (3, 6), (5, 7) y (4, 8).
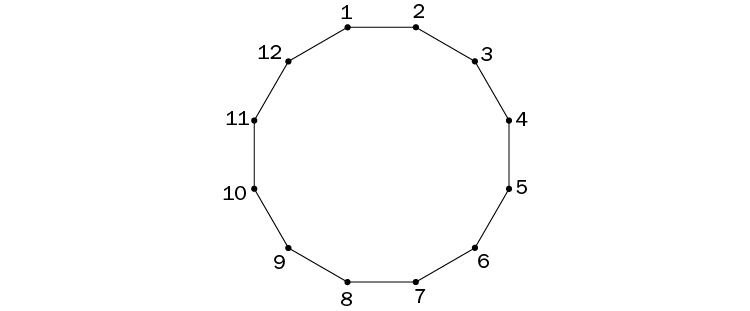
En el desafío que proponemos, utilizaremos un dodecágono regular, el polígono regular de doce lados. Numeramos sus vértices en el sentido de las agujas del reloj. Al unir vértices distintos, podemos conseguir como máximo seis segmentos de longitud distinta. El desafío consiste en averiguar si es o no posible emparejar los doce vértices, sin repetir ninguno, para obtener estos seis segmentos.
SOLUCIÓN
La solución a este desafío es que no es posible obtener los seis segmentos pedidos. Veamos por qué.
Vamos a llamar Li a la longitud del segmento que une el vértice a con el vértice a + i. Está claro que esta longitud no depende de la elección del vértice a.
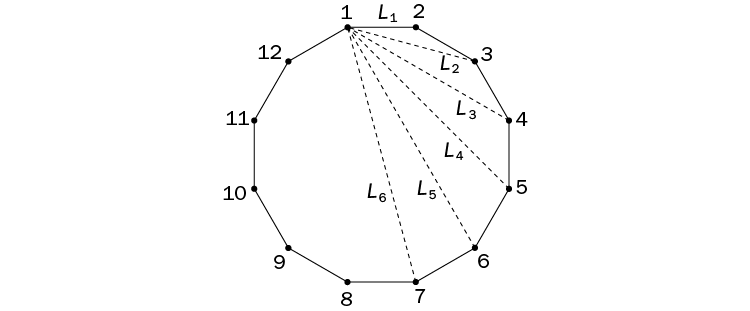
Si existiesen los seis segmentos tendrían longitudes L1, L2, L3, L4, L5 y L6.
Dibujando los segmentos sobre el dodecágono con sus vértices numerados, es obvio que los segmentos de longitud L1, L3 y L5 unirán siempre un vértice par y otro impar, así que la suma de los números marcados en estos dos vértices será un número impar. Sin embargo, los segmentos de longitud L2, L4, y L6 unirán dos vértices de la misma paridad: o bien los dos serán pares o bien los dos serán impares. Por tanto, la suma de los dos números marcados en los vértices de uno de estos segmentos será un número par.
En consecuencia, la suma de los números marcados en los doce vértices del dodecágono será la suma de los seis pares que acabamos de describir, es decir, tres números pares y tres números impares, que siempre suman un número impar. Sin embargo, los vértices no se pueden repetir, así que la suma de estos doce vértices es la suma de los números del 1 al 12, que es 78, un número par, lo cual contradice lo anterior y prueba que no es posible obtener tales segmentos.
MÁS INFORMACIÓN
Este problema, aparentemente geométrico, es en realidad un problema de paridad. De hecho se puede extender al estudio de polígonos con un número par de lados. Siempre se cumple que en un polígono regular de 2n lados solo es posible unir sus vértices, sin repetir ninguno, para obtener n segmentos de longitud distinta cuando 2n es de la forma 8k u 8k + 2. En caso de que 2n sea de la forma 8k + 4 u 8k + 6, esto no es posible.