Una cuestión
de ceros y unos

Jesús Gago Vargas

Para los primeros números naturales podemos encontrar siempre un múltiplo que solamente contiene ceros y unos. Por ejemplo,

El desafío que se plantea es probar que cualquier número N tiene un múltiplo de este tipo, formado por ceros y unos.

Solución

Primera solución

Se obtiene aplicando el conocido como principio del palomar: si hay más palomas que nidos, entonces algún nido tiene que contener al menos dos palomas.

Dado un número N, si dividimos cualquier otro número entre él, podremos obtener los restos 0, 1, 2,… N − 1 que son N restos diferentes. Estos restos van a jugar el papel de nidos, y hay N. Consideremos los números 1, 11, 111, … hasta el formado por N + 1 dígitos. Está claro que tenemos N + 1 números, que serán las palomas. Si dividimos cada uno de estos números entre N, obtenemos un conjunto de restos. Lo que es seguro es que al final tiene que haber dos números, al menos, que tienen el mismo resto tras dividirlos entre N. Ahora simplemente restamos al mayor el menor. Dicha diferencia es un número formado por unos y ceros, y cuyo resto al dividirlo por N es cero; es decir, es un múltiplo de N.

Segunda solución

Usa también el principio del palomar, y los restos de la división por N. Consideramos los números

1, 10, 100, 1000, …, 10(N − 1)

es decir, las sucesivas potencias de 10. Calculamos el resto de dividir cada uno de estos números entre N. Si alguno de ellos es cero, entonces es que la potencia de 10 correspondiente es múltiplo de N y hemos acabado. En otro caso, hay N restos sobre un total de N − 1 posibles (recordemos que hemos eliminado el caso con resto cero), por lo que dos de ellos deben coincidir. Con un poco de notación, existen dos números a y a + h tales que

10a ≡ r mód N , 10a + h ≡ r mód N con 1 ≤ r ≤ N − 1

La notación u ≡ s mód N significa que al dividir el número u entre N obtenemos el resto s. Por tanto,

10a + h ≡ r mód N , 10a + 2h ≡ r mód N , …, 10a + mh ≡ r mód N,

para cualquier número m mayor o igual que 1. Entonces

10a + 10a + h + 10a + 2h + … + 10a + (N − 1)h ≡ r + r + r + …r ≡ Nr ≡ 0 mód N.

Esto significa que el número de la izquierda, que está formado por ceros y unos, es múltiplo de N.

Tercera solución

Una demostración muy sencilla se basa en considerar el desarrollo decimal de la fracción 1/(9N).

El desarrollo decimal de una fracción es finito o periódico y a partir de él se puede obtener una fracción equivalente con denominador de la forma 10k (en el caso finito) o de la forma 9…90…0 (en el caso periódico). Si se quiere repasar cómo se hace, se puede ver en

http://gaussianos.com/expresar-un-numero-decimal-en-forma-de-fraccion/

Si 1/(9N) tuviese un desarrollo finito, sería = 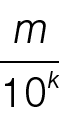, de donde 10k = 9mN ,

y 9 dividiría a una potencia de 10, lo que no puede ser (es decir, llegaríamos a
una contradicción). Por tanto, tiene que ser 1/(9N) = m / 9…90…0, de donde 9…90…0 = 9mN , y dividiendo entre 9 ambos miembros nos da 1…10…0 = mN , que es el resultado pedido.

MÁS INFORMACIÓN

Una versión de este problema apareció en la fase nacional de la Olimpiada Matemática Española del año 1993.

Una extensión del problema, apuntada por Peter Winkler en su libro Mathematical Puzzles. A Connoiseur, es que si N no es múltiplo ni de 2 ni de 5, entonces se puede encontrar un múltiplo de N que está formado solamente por unos.