Unas medias enteras

Pedro Carrión Rodríguez de Guzmán

La media aritmética de dos números se define como

.

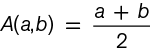Por ejemplo, A(3,7) = 5.

La media geométrica de dos números se define como

.

Por ejemplo, .

Por último, la media armónica de dos números se define como

.

Por ejemplo, .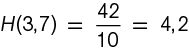

Podemos observar que no siempre la media aritmética, geométrica o armónica de números enteros es un número entero.

El desafío consiste en encontrar el menor primo p mayor que 100 para el que existe otro número entero distinto q, este no necesariamente primo, de manera que las medias aritmética, geométrica y armónica de p y q sean números naturales.

Solución

Antes de empezar a resolver el desafío vamos a recordar dos hechos sobre divisibilidad que se usarán posteriormente.

El primero es que si p es un número primo y p divide al producto m ⋅ n, necesariamente p divide a uno de los dos números.

El segundo hecho es que si m y n son dos números primos entre sí, es decir, sin un primo que divida a ambos, entonces si m divide a n ⋅ r necesariamente m divide a r.

Comencemos con la solución:

Si el entero G es la media geométrica de p y q se tiene que G2 = p ⋅ q por lo que p divide a G2, lo que implica que p divide a G. Por tanto, podemos escribir G = p ⋅ y . Tenemos, pues, que

G2 = p ⋅ q ⇒ (p ⋅ y)2 = p ⋅ q ⇒ p2 ⋅ y2 = p ⋅ q ⇒ q = p ⋅ y2.

Si A es la media aritmética de p y q, tenemos que

A = ⇒ p + q = 2A ⇒ p + p ⋅ y2 = 2A ⇒ p ⋅ (1 + y2) = 2A.

Como 2A es par y p es impar (pues es un primo mayor que 100), concluimos que
1 + y2 es par.

Por último, si H es la media armónica de p y q tenemos que

H = ⇒ H ⋅ (p + q) = 2pq ⇒ H ⋅ (p + py2) = 2p ⋅ py2 ⇒

⇒ H ⋅ p ⋅ (1+ y2) = 2p2y2 ⇒ H ⋅ (1+ y2) = 2py2.

Tenemos, pues, que 1 + y2 divide a 2py2; por otra parte 1 + y2 e y2 son números consecutivos, luego son primos entre sí. Podemos concluir entonces que 1 + y2 divide a 2p.

Recordemos que 1 + y2 es par, por lo que si 1 + y2 divide a 2p, obtenemos que

es divisor de p.

Pero p es primo, por lo que solo tiene dos divisores: 1 y p.

Como no puede ser 1 porque ello nos llevaría a que y = 1 y, por tanto, a que p = q, algo imposible pues exigimos que p y q fuesen distintos, necesariamente = p . Si encontramos el menor y impar que haga que sea primo mayor que 100, tendremos resuelto el problema. Ello se obtiene para y = 15 con lo que
p = 113 y q = 25 425.

MÁS INFORMACIÓN

Hay que señalar que el uso de la fuerza bruta para hallar p y q no garantiza que p sea ese mínimo. No se puede, por ejemplo, desechar el primo 101 tras probar valores de q menores, por ejemplo, que 100 000, pues esto no garantiza que 101 fuese el mínimo para un valor de q digamos superior a los mil trillones.

Puedes plantearte otros problemas parecidos a este. Por ejemplo, encontrar dos números enteros distintos tales que sus medias aritmética, geométrica y armónica sean enteras. ¿Cuál es la solución mínima?