Un problema con números enormes

José Manuel Bayod Bayod

Tomamos un número N que tenga cien cifras escrito en base 10. El primero de sus cien dígitos no puede ser 0, por lo demás no hay ninguna restricción. Separamos N en dos números: el formado por las cincuenta primeras cifras, A, y el formado por las restantes, B. El desafío consiste en identificar todos los números N para los que N = 3AB (el producto de 3 por A por B).

Solución

De los números N, A y B sabemos que:

• N = 3AB.

• N y A tienen, respectivamente, 100 y 50 cifras, así que A ≥ 1049 (un uno seguido de 49 ceros). B tiene 50 cifras como máximo, pero puede tener menos, puesto que es posible que la cifra N de que ocupa la posición número 51 sea un cero.

• N se obtiene poniendo B a continuación de A, completando previamente B con ceros a la izquierda si es que tenía menos de 50 cifras. Esto equivale a decir que N puede obtenerse poniendo 50 ceros a la derecha de A (es decir, multiplicándolo por 1050) y a continuación sumándole B, que así se añade a la derecha de A sin interferir con A. En otras palabras, que N = 1050A + B.

Entonces 3AB = 1050A + B, por lo que poniendo todas las A en un mismo miembro de la igualdad y sacando factor común, obtenemos A(3B − 1050) = B. El número α por el que hay multiplicar A para obtener B, α = 3B − 1050, es claramente un entero. La estrategia para resolver el desafío va a consistir en analizar con cuidado el entero α.

En primer lugar, α ha de ser positivo, puesto que α = B / A y tanto A como B son positivos. Además, α será menor que 10, pues de lo contrario B = αA tendría más de 50 cifras. Por consiguiente, α solo puede ser uno de los números 1, 2, …, 9.

Ahora que sabemos que α tiene un solo dígito pasamos a probar además que ha de ser menor que 4, por reducción al absurdo: si α fuese mayor o igual que 4, entonces

1050 + α = 3B = 3αA ≥ 12A ≥ 12 × 1049,

es decir, los números de 51 cifras, 1050 + α, que en base 10 se escribe 100…00α, y 12 × 1049, que en base 10 es 120…000, cumplirían

100…00α ≥ 120…000,

lo que es obviamente falso. (Una manera más rigurosa de llegar a una conclusión falsa sería observar que de la primera cadena de igualdades y desigualdades deduciríamos que α ≥ 12 × 1049 − 1050 = (12 − 10)1049 = 2 × 1049, pero sabemos que α es menor que 10.) Así que α solamente puede ser 1, 2 o 3.

Por último, para que el número 100…00α sea múltiplo de 3 (necesariamente lo es, puesto que es igual a 3B), la suma de sus dígitos, 1 + α, ha de ser múltiplo de 3. De los tres posibles valores de α, el único que cumple esta condición es α = 2.

Por consiguiente, la única solución posible para B (y, por tanto, para A) es la que corresponde a α = 2:

B0 = = 333…334 (con 50 cifras)

y

A0 = 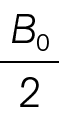= 166…667 (con 50 cifras).

El razonamiento que hemos hecho hasta ahora ha consistido en suponer que había solución y demostrar que entonces la solución solo puede ser la dada por los números A0 y B0. Nos queda comprobar que el número N0 de 100 cifras, que se obtiene al escribir primero A0 y después B0, N0 = 166…667333…334, cumple efectivamente que N0 = 3A0B0, lo cual es cierto gracias a que algunas de las implicaciones que hicimos al principio son reversibles. En efecto, la construcción de A0 y B0 nos permite concluir que N0 = 1050A0 + B0 = (1050 + 2)A0 = 3B0A0.

MÁS INFORMACIÓN

Si en lugar de números compuestos por 100 cifras estuviéramos hablando, por ejemplo, de números N de dos cifras, la primera de las cuales es A y la segunda es B, podríamos comprobar directamente que las únicas soluciones de N en la ecuación N = 3AB son 15 y 24. Pero al tratar con números tan enormes como los de 100 cifras (una búsqueda en internet del término googol nos dará una idea de la magnitud de estos números), resulta materialmente imposible, ni con medios humanos ni mecánicos, hacer una comprobación directa de todos los casos posibles.

Si sustituimos la condición de que N tenga 100 cifras por la condición más general de que tenga un número de cifras que sea par y mayor que 2, entonces la misma solución que hemos mostrado aquí es aplicable, con las modificaciones obvias.

Hay otras variantes del enunciado aquí propuesto que hacen el problema más difícil pero todavía resoluble con técnicas elementales. Entre otras, (1) suprimir la condición de que la primera de las 100 cifras sea no nula; (2) mantener las mismas condiciones pero para números escritos en una base cualquiera; (3) admitir que N pueda tener cualquier número par de cifras y además sustituir la igualdad N = 3AB por la igualdad N = λAB, donde el factor λ pueda ser cualquiera (esta última versión formó parte del Concurso de Problemas Martínez Maurica organizado por el Departamento de Matemáticas, Estadística y Computación de la Universidad de Cantabria en 1994).