
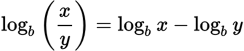
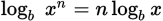
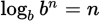 (In particular,
(In particular,
 and
and
 .)
.)For any positive base b ≠ 1 and any positive numbers x, y, and n:

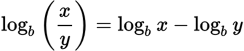
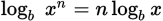
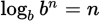 (In particular,
(In particular,
 and
and
 .)
.)For example, if logb 2 = x and logb 3 = y, then:

As you will see in Section 2-E, the third rule in KEY FACT A18 allows you to solve equations in which the variable is an exponent by bringing the variable down to the base line. To solve the equation 2x = 512, for example, take the logarithm of both sides: logb 2x = logb 512. Then
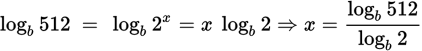
Note that what you choose for the base b does not matter. As a consequence, you might as well let b = 10. Therefore,
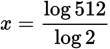 . Now use your calculator:
. Now use your calculator:
