Solutions
Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the practice tests in this book, and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you do not have to leave them out—you can almost always answer them by using one or more of the strategies discussed in Chapter 1, “Important Tactics.” The solutions given here do not depend on those strategies; they are the correct mathematical ones.
See page 15 for an explanation of the symbol ⇒, which is used in several answer explanations.
-
(D)
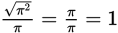 , which is a rational number. It is not irrational. Choices A, B, and C are each equal to π, which is irrational. Choice E is also irrational since
, which is a rational number. It is not irrational. Choices A, B, and C are each equal to π, which is irrational. Choice E is also irrational since
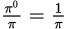 , and the reciprocal of an irrational number is irrational.
, and the reciprocal of an irrational number is irrational. -
(E)
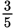 of
of
 , and 48 is
, and 48 is
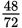 of 72.
of 72. Finally,
Finally,
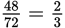 .
. -
(B) Use your calculator to convert each fraction to a decimal.

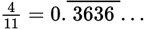 ,
,
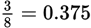 ,
,
 This is the correct order.
This is the correct order. -
(D) 0 < x < 1 ⇒ x(x) < 1(x) ⇒ x2 < x (I is true).
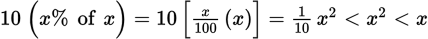 (II is true).
(II is true).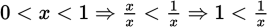 . So,
. So,
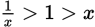 (III is false).
(III is false).Only I and II are true.
-
(D) Convert the fractions to decimals. Then the inequality becomes
 . There are infinitely many values of
. There are infinitely many values of
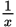 that satisfy this inequality, but
that satisfy this inequality, but
 is one obvious choice. Then
is one obvious choice. Then
 .
. -
(A)
 and
and
 . So,
. So,
 .
. -
(A)
 .
. -
(D) Since 20% of 80 is 16, Sally wants to get $80 + $16 = $96 for each sweater she sells. Then, if x is the marked price,


-
(C)
 The number of students in the school in 2020 was (1.035)10(800) = 1,128.
The number of students in the school in 2020 was (1.035)10(800) = 1,128. -
(D)
 To earn an 80% on the entire exam, Marie needs to answer a total of 64 questions correctly (80% of 80). So far, she has answered 45 questions correctly (75% of 60). Therefore, on the last 20 questions, she needs 64 – 45 =19 correct answers, and
To earn an 80% on the entire exam, Marie needs to answer a total of 64 questions correctly (80% of 80). So far, she has answered 45 questions correctly (75% of 60). Therefore, on the last 20 questions, she needs 64 – 45 =19 correct answers, and
 .
.