Solutions

Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the practice tests in this book, and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you do not have to leave them out—you can almost always answer them by using one or more of the strategies discussed in Chapter 1, “Important Tactics.” The solutions given here do not depend on those strategies; they are the correct mathematical ones.

See page 15 for an explanation of the symbol ⇒, which is used in several answer explanations.

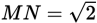1. (B) Since M and N are midpoints of sides of length 2, PM = MQ = QN = NR = 1. Since $\overline{MN}$ is the hypotenuse of an isosceles right triangle whose legs are 1, $MN=\sqrt{2}$. Similarly, $PR=2\sqrt{2}$, since it is the hypotenuse of an isosceles right triangle whose legs are 2. So, the perimeter of trapezoid PMNR is $1+\sqrt{2}+1+2\sqrt{2}=2+3\sqrt{2}$.

   

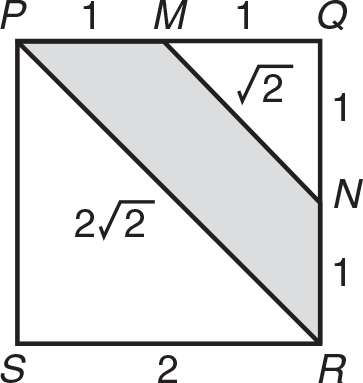
2. (A) Even if you know the formula for the area of a trapezoid (and you should), the best way to proceed is to subtract the areas of the two white triangles from 4, the area of the square. The area of $\text{△}\mathit{\text{P}}SR=\frac{1}{2}\left(2\right)\left(2\right)=2$, and the area of $\text{△}\mathit{\text{M}}QN$ is $\frac{1}{2}\left(1\right)\left(1\right)=0\text{.5}$. Therefore, the area of the shaded region is 4 – 2 – 0.5 = 1.5.

3. (A) Let x represent the side of the square. Then, the dimensions of the rectangle are (x + 5) and (x – 5), and its area is (x + 5)(x – 5) = x² – 25. Since the area of the square is 45, x² = 45, and so x² – 25 = 20.

   

4. (C) Draw and label the rhombus.

   

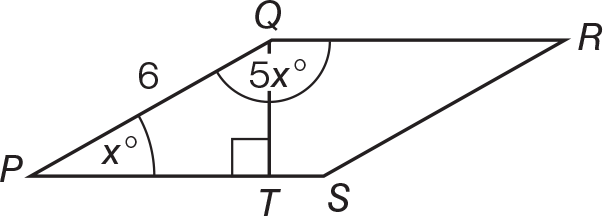
   Since angles P and Q are supplementary:

   $m\angle P+m\angle Q=180°\Rightarrow 5x+x=180\Rightarrow 6x=180\Rightarrow x=30$

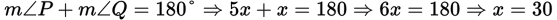
   Then, since $\text{△}\mathit{\text{P}}QT$ is a 30-60-90 right triangle, $QT=\frac{6}{2}=3$. Finally, the area of rhombus PQRS = bh = (PS)(QT) = (6)(3) = 18.

5. (D) Draw a diagram and label it.

   

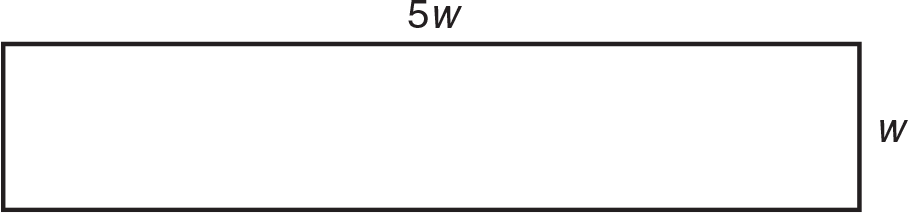
   Since the area is 180, we have 180 = 5w² ⇒ w² = 36 ⇒ w = 6. So, the width is 6, the length is 5 × 6 = 30, and the perimeter is 2(6 + 30) = 2(36) = 72.

6. (E)   By KEY FACT I2, the sum of the measures of the 10 interior angles in a decagon is (10 – 2) × 180° = 8(180°) = 1,440°. So, the average of their measures is 1,440° ÷ 10 = 144°.

7. (C) By KEY FACT I2, the sum of the angles of a pentagon is:

   $(5–2)\times 180°=3\times 180°=540°$

   Let the degree measures of the five angles be 2x, 3x, 3x, 5x, and 5x. Then:

   $540=2x+3x+3x+5x+5x=18x\Rightarrow$

   $x=(540÷18)=30$

   The degree measure of the smallest angle is 2x, and 2 × 30° = 60°.

8. (C) Since the diagonals of a square are perpendicular and congruent, and bisect each other, each small triangle is a 45-45-90 right triangle whose hypotenuse is 4. Therefore, the legs are each $\frac{4}{\sqrt{2}}=2\sqrt{2}$. So, the perimeter of each small triangle is $4+2\sqrt{2}+2\sqrt{2}=4+4\sqrt{2}$, and the sum of the perimeters is $4(4+4\sqrt{2})=16+16\sqrt{2}$.

9. (E) The sum of an interior and exterior angle is 180°. So, 180 = 9x + x = 10x ⇒ x = 18. Since the sum of all the exterior angles is 360, there are 360 ÷ 18 = 20 exterior angles, 20 interior angles, and 20 sides.

   

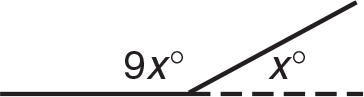
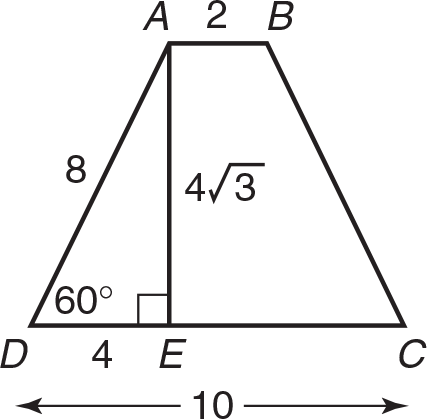
10. (C) Draw in height $\overline{AE}$. Then, $\text{△}\mathit{\text{A}}ED$ is a 30-60-90 right triangle whose hypotenuse is 8. So, DE = 4 and $AE=4\sqrt{3}$. Then, the area of trapezoid ABCD is $\frac{1}{2}\left(10+2\right)(4\sqrt{3})=6(4\sqrt{3})=24\sqrt{3}$.

    

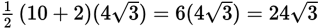11. (C) Since you do not know a formula for the area of a hexagon, you have to divide the hexagon into manageable pieces. There are many ways to do this. One way is to divide it into two trapezoids; another is to divide it into a rectangle and two triangles. The simplest way, though, is to divide it into six equilateral triangles.

    

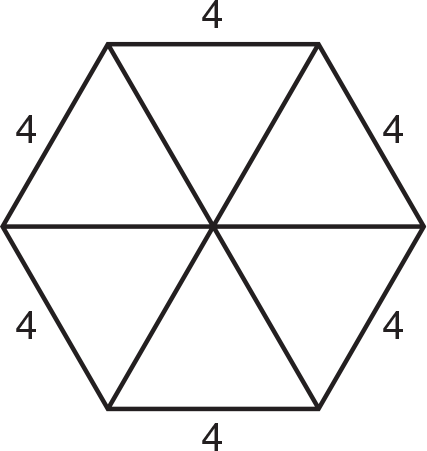
    By KEY FACT H11, the area of an equilateral triangle whose sides are 4 is 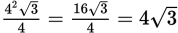$\frac{4^2\sqrt{3}}{4}=\frac{{\displaystyle 16\sqrt{3}}}{{\displaystyle 4}}=4\sqrt{3}$. So, the area of the hexagon is $6\left(4\sqrt{3}\right)=24\sqrt{3}$.

12. (C) Since you do not know a formula for the area of an octagon, you have to divide the octagon into manageable pieces. There are many ways to do that. One way is to draw four diagonals that divide the octagon into four isosceles right triangles, four rectangles, and a square.

    

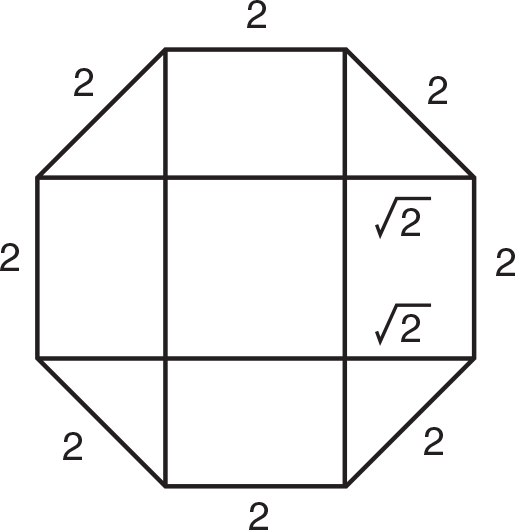
    The legs of the triangles are each 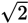$\sqrt{2}$. Therefore, each triangle has area 1, each rectangle has area $2\sqrt{2}$, and the square has area 4. Thus, the total area is $4\left(1\right)+4\left(2\sqrt{2}\right)+4=8+8\sqrt{2}$. So, a = 8, b = 8, and a + b = 16.