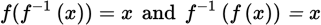
If f and g are functions such that
then we say that g is the inverse of f and write g = f–1, which is read “f inverse.” It is also true that f is the inverse of g: f = g–1.
Key Fact N7
If for some function f, f–1 exists, then:
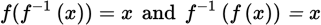
The inverse, f–1, of a function, f, undoes what f does. In Example 15, f multiplies a number by 3 and then subtracts 2 from it; g, which is f–1, adds 2 to a number and then divides the result by 3.

Not every function has an inverse, but many do. On the Math 1 test, you may be asked to find the inverse of a particular function. The procedure to do this is given in KEY FACT N8.
Key Fact N8
If f is a function of x, to find f–1, first write y = f(x). Then interchange x and y and solve for y.
So,
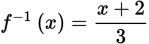 . Note that f–1, which is function g in Example 15, simply undoes what f does: f multiplies a number by 3 and then subtracts 2; f–1 adds 2 to a number and then divides the result by 3.
. Note that f–1, which is function g in Example 15, simply undoes what f does: f multiplies a number by 3 and then subtracts 2; f–1 adds 2 to a number and then divides the result by 3.