Arithmetic Sequences

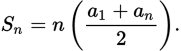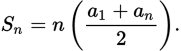
An arithmetic sequence is a sequence such as 5, 8, 11, 14, 17, . . . in which the difference between any two consecutive terms is the same. In this sequence, the difference is 3 (8 – 5 = 3; 11 – 8 = 3; 14 – 11 = 3, . . .). An easy way to find the nth term of such a sequence is to start with the first term and add the common difference n – 1 times. Here, the 5th term is 17, which can be obtained by taking the first term, 5, and adding the common difference, 3, four times: 5 + 4(3) = 17. In the same way, the 100th term is 5 + 99(3) = 5 + 297 = 302.

Key Fact Q2

If a₁, a₂, a₃, . . . is an arithmetic sequence whose common difference is d, then a_n = a₁ + (n – 1)d.

EXAMPLE 4: If the 8th term of an arithmetic sequence is 10 and the 20th term is 58, what is the first term?

Use KEY FACT Q2 twice and subtract:

$\begin{array}{ccc}{a}_{20}=a_1+19d=58 & & \\ a_8=a_1+ 7d=10 & & \\ \begin{array}{cc} \overline{ 12d=48}& \Rightarrow d=4\end{array}& & \end{array}$

Then:

$10=a_1+7d=a_1+7\left(4\right)=a_1+28\Rightarrow a_1=-18$

Key Fact Q3

If S_n represents the sum of the first n terms of the arithmetic sequence a₁, a₂, a₃, . . ., then S_n is equal to n times the average of a₁ and a_n: $S_n=n\left({\displaystyle \frac{a_1+a_n}{2}}\right)\text{.}$

EXAMPLE 5: What is the sum of the first 50 odd positive integers?

The odd positive integers 1, 3, 5, . . . form an arithmetic sequence, whose common difference is 2. The first and 50th terms, a₁ and a₅₀, are 1 and 99, respectively. So, by KEY FACT Q3, S₅₀, the sum of the first 50 odd positive integers is equal to $50\left(\frac{1 + 99}{2}\right)=50\left(50\right)=\mathrm{2,500}.$