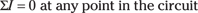Chapter 2

Gearing Up for Physics II

In This Chapter

Mastering units and math conventions

Reviewing foundational Physics I concepts

This chapter prepares you to jump into Physics II. If you’re already a physics ace, there’s no need to get bogged down here — just fly into the physics topics themselves, starting with the next chapter. But if you’re not fast-tracked for the physics Nobel Prize, it wouldn’t hurt to scan the topics here, at least briefly. Doing so can save you a lot of time and frustration in the chapters coming up.

Math and Measurements: Reviewing Those Basic Skills

Physics excels at measuring and predicting the real world, and those predictions often come though math. So to be a physicsmeister, you have to have certain skills down cold. And because this is Physics II, I assume that you’re somewhat familiar with the world of physics and some of those basics already. You look at those skills here in refresher form (if you’re unclear about anything, check out a book like Physics For Dummies (Wiley) to get up to speed).

The following skills are pretty basic; you can’t get through Physics I without them. But make sure you have at least a passing acquaintance with the topics in this section — especially if it’s been quite some time since Physics I.

Using the MKS and CGS systems of measurement

The most common measurement systems in physics are the centimeter-gram-second (CGS) and meter-kilogram-second (MKS) systems. The MKS system is more common. For reference, Table 2-1 lists the primary units of measurement, along with their abbreviations in parentheses, for both systems.

Table 2-1 Metric Units of Measurement
Type of Measurement	CGS Unit	MKS Unit
Length	Centimeters (cm)	Meters (m)
Mass	Grams (g)	Kilograms (kg)
Time	Seconds (s)	Seconds (s)
Force	Dynes (dyn)	Newtons (N)
Energy (or work)	Ergs (erg)	Joules (J)
Power	Ergs/second (erg/s)	Watts (W) or joules/second (J/s)
Pressure	Baryes (Ba)	Pascals (Pa) or newtons/square meter (N/m2)
Electric current	Biots (Bi)	Amperes (A)
Magnetic field	Gausses (G)	Teslas (T)
Electric charge	Franklins (Fr)	Coulombs (C)

These are the primary measuring sticks that physicists use to measure the world with, and that measuring process is where physics starts. Other measuring systems, such as the foot-pound-second (FPS) system, are around as well, but the CGS and MKS systems are the main ones you see in physics problems.

Making common conversions

Measurements don’t always come in the units you need them in, so doing physics can involve a lot of conversions. For instance, if you’re using the meter-kilogram-second system (see the preceding section), you can’t plug measurements in centimeters or feet into your formula — you need to get them in the right units first. In this section, I show you some values that are equal to each other and an easy way to know whether to multiply or divide when doing conversions.

Looking at equal units

Converting between CGS (centimeter-gram-second) and MKS (meter-kilogram-second) units happens a lot in physics, so here’s a list of equal values of MKS and CGS units for reference — come back to this as needed:

Length: 1 meter = 100 centimeters

Mass: 1 kilogram = 1,000 grams

Force: 1 newton = 105 dynes

Energy (or work): 1 joule = 107 ergs

Pressure: 1 pascal = 10 barye

Electric current: 1 ampere = 0.1 biot

Magnetism: 1 tesla = 104 gausses

Electric charge: 1 coulomb = 2.9979 × 109 franklins

Converting back and forth between MKS and CGS systems is easy, but what about other conversions? Here are a some handy conversions that you can come back to as needed. First, for length:

1 meter = 1,000 millimeters

1 inch = 2.54 centimeters

1 meter = 39.37 inches

1 mile = 5,280 feet = 1.609 kilometers

1 kilometer = 0.62 miles

1 angstrom (Å) = 10–10 meters

Here are some conversions for mass:

1 slug (foot-pound-second system) = 14.59 kilogram

1 atomic mass unit (amu) = 1.6605 × 10–27 kilograms

These are for force:

1 pound = 4.448 newtons

1 newton = 0.2248 pounds

Here are some conversions for energy:

1 joule = 0.7376 foot-pounds

1 British thermal unit (BTU) = 1,055 joules

1 kilowatt-hour (kWh) = 3.600 × 106 joules

1 electron-volt = 1.602 × 10-19 joules

And here are conversions for power:

1 horsepower = 550 foot-pounds/second

1 watt = 0.7376 foot-pounds/second

Using conversion factors: From one unit to another

If you know that two values are equal to each other (see the preceding section), you easily use them to convert from one unit of measurement to another. Here’s how it works.

First note that when two values are equal, you can write them as a fraction that’s equal to 1. For instance, suppose you know that there are 0.62 miles in a kilometer:

1 km = 0.62 miles

You can write this as

or

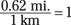
Each of these fractions is a conversion factor. If you need to go from miles to kilometers or kilometers to miles, you can multiply by a conversion factor so that the appropriate units cancel out — without changing the value of the measurement, because you’re multiplying by something equal to 1.

For instance, suppose you want to convert 30 miles to kilometers. First, write 30 miles as a fraction:

Now you need to multiply by a conversion factor. But which version of the fraction do you use? Here, miles is in the numerator, so to get the miles to cancel out, you want to multiply a fraction that has miles in the denomina-

tor. Because 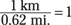, you can multiply 30 miles by that fraction without

changing the measurement. Then the miles on the bottom cancels the miles on the top:

Always arrange your conversion factors so that you cancel out the part of the unit you want to swap out for something else. Each unit that you don’t want in your final answer has to appear in both a numerator and a denominator.

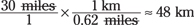
Sometimes you can’t do a conversion in one step, but you can string together a series of conversion factors. For instance, here’s how you can set up a problem to convert 30 miles per hour to meters per second. Notice how I multiply by a series of fractions, making sure that every unit I want to cancel out appears in the numerator of one fraction and the denominator of another.

Doing speedy metric conversions

In the metric system, one unit can be used as a basis for a broad range of units by adding a prefix (Table 2-2 shows some of the most common prefixes). Each prefix multiplies the base unit by a power of 10. For example, kilo- says that the unit is 1,000 times (103 times) larger than the base unit, so a kilometer is 1,000 meters. And milli- means the unit is 0.001 times (10–3) smaller than the base unit. This means that converting from one metric unit to another is usually a matter of moving the decimal point.

Table 2-2 Metric Prefixes
Prefix	Symbol	Meaning (Decimal)	Meaning (Power of Ten)
Nano-	n	0.000000001	10–9
Micro-	μ	0.000001	10–6
Milli-	m	0.001	10–3
Centi-	c	0.01	10–2
Kilo-	k	1,000	103

By finding the difference in exponents on the power of 10 of your original units and the units you want to convert to, you can figure out how many places to move the decimal point.

For instance, say you have a distance of 20.0 millimeters, and you’d prefer to express it in centimeters. You know that 1 millimeter is 10–3 meters, and 1 centimeter is 10–2 meters (as Table 2-2 shows). If you find the difference in exponents, you see that –3 –(–2) = –1. The answer is negative, so you just have to move the decimal point one place to the left (for a positive answer, you move it to the right). Thus, 20.0 millimeters is equal to 2.00 centimeters.

Using temperature-conversion equations

You can use the following equations to convert between the different units of temperature:

Kelvin temperature = Celsius temperature + 273.15

Celsius temperature = 5//9(Fahrenheit temperature – 32°)

Keeping it short with scientific notation

Physicists often delve into the realms of the very small and the very large. Fortunately, they also have a very neat way of writing very large and very small numbers: Scientific notation. Essentially, you write each number as a decimal (with only one digit to the left of the decimal point) multiplied by 10 raised to a power.

Say you want to write down the speed of light in a vacuum, which is about three hundred million meters per second. This is a three followed by eight zeros, but you can write it as just a 3.0 multiplied by 108:

300,000,000 m/s = 3.0 × 108 m/s

You can write small numbers by using a negative power to shift the decimal point to the left. So if you have a distance of 4.2 billionths of a meter, you could write it as

0.0000000042 m = 4.2 × 10–9 m

Note how the 10–9 moves the decimal point of the 4.2 nine places to the left.

Brushing up on basic algebra

To do physics, you need to know basic algebra. You’re going to be slinging some equations around, so you should be able to work with variables and move them from one side of an equation to the other as needed, no problem.

You don’t need to be bogged down or daunted by the formulas in physics — they’re only there to help describe what’s going on in the real world. When you see a new formula, consider how the different parts of the equation relate to the physical situation it describes.

Take a simple example — the equation for the speed, v, of an object that covers a distance Δx in a time Δt (Note: The symbol Δ means “change in”):

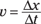
Before you go any further, try relating the parts of this equation to what you intuitively understand about speed. You can see in the equation that if Δx increases, then v increases — if you cover a greater distance in a given time, then you’re traveling faster. You can also see that if Δt (in the denominator of the fraction) increases, then v decreases — if it takes you longer to cover a given distance, then you’re moving more slowly.

If you need to, you can rearrange an equation algebraically to isolate the part you’re interested in. That way, you can get a feel for how other variables affect each other. For instance, see what the equation means for travel time by rearranging it to isolate Δt:

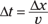
Now you can see that Δt increases as Δx increases, and Δt decreases as v increases. This just means that travel time increases if you have to travel farther and decreases if you travel faster.

Using some trig

You work with some angles to this book — such as those you have to figure out when light bounces off mirrors or bends in lenses. To handle angles and related distances, you need some trigonometry.

Pretty much everything in trig comes down to the right triangle. For example, take a look at the right triangle in Figure 2-1. The two shorter sides, or legs, are called x and y (because they lie along the x- and y-axes respectively), and the longest side, across from the 90° angle, is the hypotenuse. One of the other internal angles is marked θ.

Figure 2-1: The two legs (x and y) and hypotenuse (h) of a right triangle.

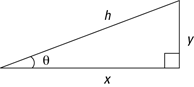
Here’s one important formula to know: the Pythagorean theorem. It relates the lengths of x, y, and h, so given the lengths of two sides, you can find the length of the third:

x2 + y2 = h2

To work with angles (such as θ), you need the trig functions sine, cosine, and tangent. To find the values of trig functions, just divide one side of the triangle by another. Here’s what it looks like:

Sine: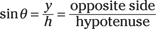

Cosine: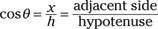

Tangent: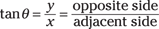

Note that these equations relate any two sides of a right triangle to the angle that’s between the hypotenuse and one of the other sides. So if you know θ and one of the other sides, you can use some algebra (and your calculator) to find the length of any other side.

To find the angle θ, you can go backward with inverse sines, cosines, and tangents, which are written like this: sin–1, cos–1, and tan–1. If you make the appropriate fraction out of two known sides of a triangle and take the inverse sine of that (sin–1 on your calculator), it’ll give you back the angle itself. Here’s how the inverse trig functions work (see Figure 2-1 for which sides are x, y, and h):

Inverse sine:

Inverse cosine: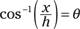

Inverse tangent:

Physicists use sine and cosine functions to describe real-world waves and alternating current and voltage. I introduce waves in Chapter 6, and I cover alternating current (AC circuits) in Chapter 5.

Using significant digits

You may be surprised to hear that physics isn’t an exact science! It can be pretty accurate, but nothing is ever measured perfectly. The more accurately the quantity is measured, the more digits you know. The digits you know are the significant figures. For instance, a stopwatch measurement of 11.26 seconds has four significant figures. Here are a few guidelines for figuring out what’s significant:

For a decimal less than 1, everything that follows the first nonzero digit is significant. For example, 0.0040 has two significant digits.

For a decimal greater than 1, all digits, including zeros after the decimal point, are significant. For instance, 20.10 has four significant digits.

For a whole number, the non-zero digits are significant. Any number of trailing zeros also may be significant.

So how do you show the accuracy of a measurement such as 1,000 meters, which ends in zeros? You may know anywhere between one and four digits from your measurements. The best way to clear this up is to use scientific notation. For instance, if you write 1,000 as 1.000 × 103, with three zeroes after the decimal point, the number has four significant figures — you measured to the nearest meter. If you write it as 1.00 × 103, with two zeroes after the decimal point, the number has three significant figures — you measured to the nearest ten meters. (For info on scientific notation, see the earlier section “Keeping it short with scientific notation.”)

When you do calculations with numbers that are known only to a particular accuracy, then your answer is also only of a particular accuracy. After you do all your calculations, you need to round the answer. Here are some simple rules you can apply:

If you multiply or divide two numbers: The answer has the same number of significant figures as the least-accurate of the two numbers being multiplied or divided. For example, consider the following calculation:

12.45 × 0.050 = 0.6225

Because 0.050 has two significant figures, you round the answer to 0.62.

If you add or subtract two numbers: The answer has the same number of decimal places as the least-accurate of the two numbers you’re adding or subtracting. For example, consider

11.432 + 1.3 = 12.732

Because the least-accurate number, 1.3, has only one decimal place, write the answer as 12.7.

Refreshing Your Physics Memory

To make progress, physics often builds on previous physics advances. For example, knowing about vectors is important not just to handle problems with acceleration (that’s Physics I) but also to help you track charged particles in magnetic fields (that’s Physics II).

In this section, you take a down-memory-lane tour of some Physics I concepts that pop up again in Physics II. If you don’t feel comfortable with these topics, check out a physics text to make sure you’re up to speed in Physics I before proceeding.

Pointing the way with vectors

Vectors are the physics way of pointing a direction. A vector has a direction and a magnitude (size) associated with it — the magnitude is the vector’s length.

You usually see the names of vectors in bold in physics. Figure 2-2 shows vector A. That’s just a standard vector, and it may stand for, say, the direction an electron is traveling in. The length of the vector may indicate the speed of the electron — the faster the electron is going, the longer the vector.

Figure 2-2: The components of a vector.

You don’t see lots of vectors in this book (did I just hear a sigh of relief?), but you should know how to break a vector like A up into its components along the x- and y-axes (you need to do this in Chapter 4 for the magnetic field and in Chapter 5 for alternating currents and voltages).

If you’re given the length of the vector (its magnitude, labeled A in Figure 2-2) and the angle θ (its direction), breaking a vector into its components works like this:

Ax = A cos θ

Ay = A sin θ

where Ax is the x component of vector A and Ay is the vector’s y component. (This is really just a bit of trig, where Ax and Ay are the legs of the triangle and A is the hypotenuse — see the earlier section “Using some trig” for info on the sine and cosine functions.)

Resolving vectors into components is particularly useful if you have to add two vectors, A + B. You break them up into their separate components and then add those components to get the components of the vector sum, which is a new vector you can call C:

Cx = Ax + Bx

Cy = Ay + By

When you have the components of a vector like C, you can covert them into a length (magnitude) for C (written as 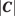) and an angle for C this way:

Magnitude of C:

Note: This is just the Pythagorean theorem solved for the hypotenuse .

Direction of C:

See the earlier section “Using some trig” for info on inverse trig functions.

So now you’re able to go from representing a vector in terms of its length and angle to its components and then back again — a very handy skill to have.

Moving along with velocity and acceleration

This book has a little to say about velocity and acceleration. For example, you work with them when a magnetic field diverts electrically charged particles from the direction in which they’re traveling.

Both velocity and acceleration are vectors, v and a respectively. Velocity is the change in the position-vector divided by the time that change took. For example, if the position of a ping-pong ball is given by the position-vector x, then the change in the position (Δx) divided by the amount of time that change took (Δt) is the velocity:

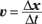
As a vector, velocity has a direction. The magnitude of the velocity vector is the speed, which has a size but not a direction. That is, velocity is a vector, but speed isn’t.

If the velocity isn’t staying constant, the ping-pong ball is undergoing acceleration. Acceleration is defined as the change in velocity divided by the time that change takes, or

Note that a change in direction is considered a change in velocity, so something can be accelerating even if its speed doesn’t change.

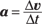
Velocity is commonly measured in meters per second (m/s) — which means that acceleration’s units are commonly meters per second squared (m/s2).

Strong-arm tactics: Applying some force

When an electron enters an electric field, it gets pushed one way or another — that is, it experiences a force. Physics I has a lot to say about force — for example, here’s the famous equation that relates total force (F), mass (m), and acceleration (a) (note that acceleration and force are both vectors):

F = ma

So to find out how much force is acting on the electron to push it along (and you don’t need much, because electrons don’t weigh very much), you’d put in the electron’s acceleration and its mass, and you’d get the total force acting on it. The formula also shows that applying a force to something can make it accelerate, and you see that idea used every now and then in this book.

The units of force you see most commonly are newtons (in the meter-kilogram-second system), symbol N, named for Sir Isaac Newton (the fellow with the falling apple acted on by the force of gravity).

Getting around to circular motion

Charged particles in magnetic fields travel in circles, so you need to know something about circular motion in Physics II. Physics I has plenty to say about circular motion. For example, take a look at Figure 2-3, where an object is traveling in circular motion.

The velocity of an object moving in a circle points along the circle of its path — this is called the tangential direction. The force that keeps the object moving in a circle points toward the center of the circle — in a direction that’s at right angles to the velocity. For instance, when you spin a ball on a string, the string can exert a force on the ball only in the direction that’s along its length, perpendicular to the path of the ball; this is what causes the ball to move in a circular path.

Figure 2-3: Circular motion.

The angle that an object moving in circular motion covers in so many seconds is its angular velocity, ω:

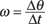
Here, the angle θ is measured in radians, so the units of angular velocity are radians/second. (Note: Exactly 2π radians are in a complete circle, which means that 2π radians equals 360°, or each radian is 360° ÷ 2π degrees.)

If the object is speeding up or slowing down, it’s undergoing angular acceleration, which is given the symbol α. Angular acceleration is defined as the change in angular velocity (Δω) divided by the time that change took (Δt):

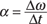
The units of angular acceleration are radians/second2.

In circular terms, force becomes torque, with the symbol τ (also a vector, of course), where the magnitude of torque equals force multiplied by distance and the sine of the angle between them:

τ = Fr sin θ

And the counterpart of mass in circular terms is the moment of inertia, I. Newton’s law, force = mass × acceleration, becomes this in circular terms:

τ = Iα

That is, torque = moment of inertia × angular acceleration.

Even linear kinetic energy has an alter ego in the circular world, like this:

You can have angular momentum, L, as well:

L = Iω

Getting electrical with circuits

Physics I introduces the idea of circuits, at least simple circuits with batteries. The rules of resistance and Kirchoff’s rules, which I review in this section, form the basis for describing the currents and voltages in circuits. You need these rules whenever you work out the various currents and voltages. For example, in Chapter 5, you use them for a simple circuit with three elements in series. You can find a more thorough description of these rules in Physics For Dummies.

According to Ohm’s law, you can determine the current going through any resistor with the following equation, where I is the current measured in amperes, V is the voltage across the resistor measured in volts, and R is the resistance of the resistor measured in ohms (Ω):

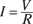
That helps with individual resistors, but what about when they’re assembled into a circuit as Figure 2-4 shows? There, you can see three resistors with resistances of 2 Ω, 4 Ω, and 6 Ω. The currents in each wire, I1, I2, and I3, are driven by the two batteries, which generate voltages of 12 volts and 6 volts.

Figure 2-4: A circuit with two loops.

To solve for the currents and voltages, you use Kirchoff’s rules:

The loop rule: The sum of voltages (ΣV) around a loop — any loop in the circuit — is zero:

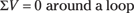
The junction rule: The sum of all currents (ΣI) into any point in the circuit must equal the sum of all currents out of that point (that is, the net sum of all currents into and out of any point in the circuit must be zero):