Chapter 3

Getting All Charged Up with Electricity

In This Chapter

Understanding charges

Examining electric forces and Coulomb’s law

Finding electric field

Finding electric potential

Understanding electric potential and capacitors

This chapter is dedicated to things that go zap. Chances are that your day-to-day life would be very different without electrical appliances from the computer to the light bulb. But electricity is even more important than that; it’s a physical interaction that’s fundamental to how the whole universe works. For example, chemical reactions are all basically of an electrical nature, and without electricity, atomic matter — the world as you know it — could not exist.

Even though electricity is integral to the existence of all the complicated constructions of matter and chemistry, it has a simple and beautiful nature. In this chapter, you see what makes static electricity, electric fields, and electric potential work.

Understanding Electric Charges

Where does electric charge come from? It turns out to be built into all matter. An atom is made up of a nucleus and electrons in orbit around the nucleus, and the nucleus is made up of protons and neutrons. The protons have a positive charge (+), and the electrons a negative charge (–). So you have electric charges inside any piece of matter you care to name.

What can you do with that charge? You can separate charges from each other and so charge up objects with an excess of one charge or another. Those separated charges exert forces on each other. In this section, I discuss all these concepts — and more — about electric charges.

Can’t lose it: Charge is conserved

Here’s an important fact about charge: Just as you can’t destroy or create matter, you can’t create or destroy charge. You have to work with the charge you have.

Because charge can’t be created or destroyed, physicists say that charge is conserved. That is, if you have an isolated system (that is, no charge moves in or out of the system), the net charge of the system stays constant.

Notice that the conservation of charge says the net charge remains constant — that is, the sum of all charges stays the same. The actual distribution of charges can change, such as when one corner of a system becomes strongly negatively charged and another corner becomes positively charged. But the sum total of all charge — whether you’re talking about the whole universe or a smaller system — remains the same. No charge in or out means the charge of the system remains constant.

Measuring electric charges

Electric charges are measured in coulombs (C) in the MKS system, and each electron’s charge — or each proton’s charge — is a tiny amount of coulombs. The proton’s charge is exactly as positive as the electron’s charge is negative.

The electric charge of a proton is named e, and the electric charge of an electron is –e. How big is e? It turns out that

e = 1.60 × 10–19 C

That’s really tiny. Here’s how many electrons make up 1 coulomb:

So there are 6.25 × 1018 electrons in 1 coulomb of (negative) charge.

Opposites attract: Repelling and attracting forces

An uncharged atom is composed of as many electrons as protons. These stay together because of the mutual attraction of these positively and negatively charged components. That’s why all ordinary matter doesn’t instantly disintegrate before your very eyes.

Objects that have the same charge (– and – or + and +) exert a repelling force on each other, and objects that have opposite charges (+ and –) attract each other (you’ve always heard that opposites attract, right?). For example, take a look at Figure 3-1, where two suspended ping-pong balls are being charged in various ways.

Figure 3-1: Force between charges.

In Figure 3-1a, the two ping-pong balls have the same, negative charge. They’re exerting a repelling force on each other, forcing them apart. And the funny thing is that they’ll stay that way indefinitely, no additional action or batteries needed — the static charge on each ping-pong ball just stays there.

Actually, it’s not totally true that the charge on each ping-pong ball just stays there. In fact, charge is continually being transferred from charged objects to the water molecules in the air, which carry it off. On humid days, charged objects actually lose their charge faster.

In Figure 3-1b, the two ping-pong balls have opposite charges, – and +, so they attract each other. Note that if they were to touch, charge would flow and the two ping-pong balls would each end up with the same charge. If the + charge is the same magnitude as the – charge, that means that the balls would end up electrically neutral and would just hang down straight.

In Figure 3-1c, the two ping-pong balls have the same positive charge, so once again they repel each other. The force repelling the two ping-pong balls is the same as that in Figure 3-1a if the positive and negative charges have the same magnitude (just different signs).

Putting charges to work: The story on photocopiers

Many areas of modern life depend on electrical charges — and not just flowing electricity. Static electricity plays a role as well. For example, take a photocopier, which makes copies through a process called xerography (from the Greek words xeros and graphos, which mean “dry writing”).

Here’s how a photocopier works: A drum with a surface that contains the element selenium (Se) does the actual printing — selenium is used because of its electrical properties in response to light. The drum is given a positive charge, evenly distributed over the drum’s surface.

Next, an image of the document to be copied is focused on the drum, which revolves to catch the light that’s scanning along the document. The image forms light and dark areas on the drum — and here’s the tricky part: The dark parts retain their positive charge, but thanks to the properties of selenium, the light areas become conducting, and their positive charge is conducted away, leaving them neutral.

In the next step, dry toner (powder of the color you’re printing — black powder in a black-and-white copier) is given a negative charge and sprayed onto the drum. The negatively charged toner sticks to the positively charged areas of the drum (which mimic the dark areas of the document), producing a mirror image of the document in toner on the drum.

The drum is then pressed against a blank piece of paper, and the toner on the drum adheres to the paper. The paper is then passed through heated rollers to fix the toner onto the paper. And there you have your copy, all thanks to the ability of opposite charges to attract each other.

Getting All Charged Up

In this section, you see how to deliver charge to objects. I let it sit there a while, and you experience charge in a way that really makes your hair stand on end: static electricity. I also transfer charge from object to object, and I let it flow nice and smoothly through wires.

Static electricity: Building up excess charge

You may not be able to create or destroy charges, but you can move them around and create imbalances within a system. When you charge up an object, you keep adding more and more charges to the object, and if that charge has nowhere to go, it just accumulates. Static electricity is the kind of electricity that comes from this excess charge.

Everyone’s familiar with the unpleasant experience of walking across a rug and then getting zapped by a doorknob. What’s actually happening there? Turns out that you’re actually picking up spare electrons from the rug. Your body collects an excess of electrons, and when you touch the doorknob, they flow out of you. Ouch!

Protons, being bound inside the nucleus, aren’t really free to flow through matter, so when you charge something, it’s usually the electrons that are moving around and redistributing themselves. When something gets charged negatively, electrons are added to it. When it gets charged positively, electrons are taken away, leaving the protons where they are, and the net surplus of protons makes a positive charge.

Before you’re zapped, that excess of charge is static electricity: It’s electricity because it’s made up of electrical charges, and it’s called static electricity when it isn’t flowing anywhere. When you’re charged with static electricity, each of the hairs on your head carries a share of this excess of electrons. You may develop a spiky new hairstyle as each hair repels its neighbor (which has the same charge). Your hair quickly returns to normal if you touch something that the excess electrons can flow into. They quickly rush through the contact point, giving you the shock.

Though charge can flow through your fingertip, you usually find it flowing through wires in a circuit, where it doesn’t build up. In circuits, charge doesn’t collect and remain stationary, because it’s always free to flow (however, I show you an exception to this idea in the later section “Storing Charge: Capacitors and Dielectrics”).

But when electricity gets blocked and yet still piles up — it can’t go anywhere — then you have static electricity. If the electricity in a circuit is like a river of electricity that keeps flowing around and around (kept in motion by, say, a battery), then static electricity is like a river of electricity that’s dammed up — but charges keep getting added. So although charges don’t build up in circuits, they do build up when you have static electricity.

Checking out charging methods

In this section, I cover two ways to charge objects: by contact and by induction. These are simple physical mechanisms that can help you understand how charge behaves and how it can be redistributed.

Charging by contact

Charging by contact is the simplest way of charging objects — you just touch the object with something charged and zap! The object becomes charged. No big mystery here.

For example, take a look at Figure 3-2 — a negatively charged rod is brought into contact with a ball that’s originally neutral. The result? The ball is left with a negative charge. That’s because the electrons in the rod are always pushing each other (because like charges repel), so they’re always looking for ways to redistribute themselves farther apart. When the rod comes in contact with the ball, some of the electrons take the opportunity to slip off the rod and onto the ball. Presto! The ball gets charged. (Note: For this to happen, the electrons need to be free to flow through the materials, which can happen if the materials are conductors. Materials that don’t allow electrons to flow through them are insulators. I discuss both types of materials later in “Considering the medium: Conductors and insulators.”)

Figure 3-2: Charging by contact.

Touch a negatively charged glass rod to a neutral ping-pong ball, and the ball acquires a negative charge by contact. But you may wonder how to charge the glass rod in the first place. You can do this in many ways, but the simplest and oldest way is to take a glass rod and some silk and rub the two together. A transfer of electrons from one material to the other occurs due to molecular forces between the two types of material. Different materials have different propensities to exchange electrons — you may have noticed that a balloon and a wool sweater work well.

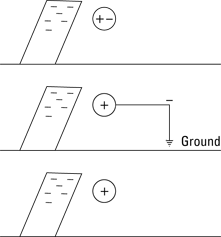
Charging by induction

You can deliver charge to an object indirectly using induction. Here’s how charging by induction works: You bring a charged rod close to a neutral object. Say the rod is charged negatively — the negative charges (electrons) in the neutral object are repelled to the opposite side of the object, leaving a net positive charge close to the rod, as Figure 3-3 shows at the top.

Now comes the clever part: You connect the far side of the object to the ground. Just connect a wire from the far side of the object to the actual Earth, which acts as a huge reservoir of charge. The negative charges — the electrons — that are being forced to the far side of the object are frantic to get off the object, because the charge on the rod is repelling them. By connecting the far side of the object to the ground with a wire, you provide those electrons with an escape route. And the electrons take that escape route by the millions and trillions.

Then you cleverly disconnect the wire from the far side of the object. The electrons that wanted to get away have fled — and now there’s nowhere else for any other charges to go. The result is that the object is left with a positive charge, because you’ve drained off much of the negative charge that was being pushed by the rod. And you haven’t lost any of the charge on the glass rod.

The upshot is that the object is left with the opposite charge of the rod. And that’s charging by induction. Pretty cool, eh?

Figure 3-3: Charging by induction.

Lightning rods work through induction. In thunderclouds, charges get separated from the top to the bottom of the cloud, so the top and the bottom of the cloud become strongly charged. When lightning strikes, the charge on the bottom of the cloud is zapping the Earth. If you have a lightning rod, the strong charge on the bottom of the cloud induces the opposite charge on the lightning rod (which is connected to the ground). When lightning strikes, it’s attracted to that opposite charge and hits the lightning rod.

Considering the medium: Conductors and insulators

You’re probably familiar with the concepts of electrical conductors — like the copper wire in an extension cord — and electrical insulators — like the plastic that coats the electrical wire and prevents the electricity in the wire from delivering a nasty shock. In this section, you take a closer look at conductors and insulators in physics terms.

Say you have two charged objects some distance apart from each other. They’re not losing charge; they’re just sitting there. Then you bring a piece of rubber and touch both of them with the rubber. What happens? Nothing, because rubber is an electrical insulator; electricity is conducted through rubber only with difficulty.

Now say that you bring a copper bar in contact with the two objects — immediately, charge flows from one to the other, because copper is an electrical conductor.

Good electrical conductors consist of atoms for which the outermost electrons are not very tightly bound, so they can easily hop from atom to atom and take part in an electric current. The electrons in the very outer orbit around the nucleus are called valence electrons, and those are the ones that can detach from atoms and roam freely through the conductor. (Interestingly, materials that are good electrical conductors, like most metals, are usually also good thermal conductors.)

Current is always defined as the direction of the flow of positive charges, but in reality, it’s the electrons that do the moving and therefore transport electrical charge. In this case, electrons move from the negatively charged object to the positively charged object. But if you want to draw the direction of the current, that goes from the positively charged object to the negatively charged one. Historically, this convention was adopted before people knew that electrons, not positive charges, carry the current.

Coulomb’s Law: Calculating the Force between Charges

Coulomb’s law is one of the physics biggies. That’s the same Coulomb (Charles-Augustin de Coulomb) that the unit of charge, the coulomb, is named after, so you know Coulomb’s law has to be some serious stuff.

And serious stuff it is: Charges can attract or repel each other, and Coulomb’s law lets you calculate the exact force that two point charges a certain distance away will exert on each other. A point charge just has all its charge concentrated in a single point, with no surface area that the charge can be distributed over. Point charges are particularly beloved by physicists because they’re easy to work with.

Say you have two point charges, with opposite signs, attracting each other from a certain distance r apart. What’s the force between the two charges? Coulomb has the answer: His law says that if the charge of one charge is q1 and the charge of the other charge is q2, then the force between the two charges is

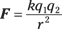
In this equation, k is a constant, and its value is 8.99 × 109 N-m2/C2; q1 and q2 are the charges, in coulombs (C), of the charged objects doing the attracting or repelling; r is the distance between the charges; and F is the electrostatic force between the charges.

Force is a vector, so when you’re looking at point charges, the direction of the force is always along a line between the two charges (assuming there are only two) and

Toward each other if the charges have opposite signs (that is, the force has a negative sign)

Away from each other if the charges have opposite signs (that is, the force has a positive sign)

Introducing Electric Fields

Electric field is the field in space created by electric charges. When two charges attract or repel each other, their electric fields are interacting.

Charge can be distributed in many ways. You can have point charges, sheets of charge, cylinders of charge, and many more configurations. Coulomb’s law, which I discuss earlier in “Coulomb’s Law: Calculating the Force between Charges,” works only for point charges. So how do you handle force for other distributions of charge? You often use electric fields, which I discuss in this section.

Sheets of charge: Presenting basic fields

How do you calculate force for a sheet of charge? Instead of modifying Coulomb’s law to handle sheets of charge, you can simply measure the force that the sheet of charge exerts on a small positive test charge. From there, you know how much force per coulomb the sheet of charge is capable of exerting, and when you have your own charge, which may be positive or negative, you can simply multiply the force per coulomb by the size of your charge.

The idea of measuring force per coulomb to handle non-point charges got to be very popular and became known as the electric field. Here’s the definition: Electric field (E) is the force (F) that a small test charge would feel due to the presence of other charges, divided by the test charge (q):

Electric field’s units are newtons per coulomb (N/C), and electric field is a vector. The direction of the electric field at any point is the force that would be felt by a positive test charge.

What’s that in plain English? Electric field is just the force per coulomb that a charge would feel at any point in space. You divide out the test charge to leave you just newtons per coulomb, which you can multiply by your own charge to determine the force that charge would feel.

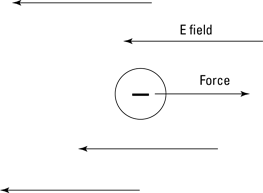
For example, say you’re walking on a wool carpet and pick up a static electricity charge of –1.0 × 10–6 coulombs. You suddenly encounter a 5.0 × 106 N/C electric field in the opposite direction in which you’re walking, as Figure 3-4 shows.

Figure 3-4: The force on a charge in an electric field.

How big of a force do you feel? Well, the electric field is 5.0 × 106 newtons per coulomb and you have a charge of –1.0 × 10–6 coulombs, so you get the following:

F = qE = (–1.0 × 10–6 C)(5.0 × 106 N/C) = –5.0 N

That is, you feel a force of 5.0 N, and the minus sign means that the force is in the direction opposite of the electric field. That’s a little more than 1 pound of force.

So that’s what electric field tells you — how much electric influence is in a given region, ready to cause a force on any charge you bring into the electric field.

Note that the electric field has a direction. How can you tell which way the force that an electric field causes will push the charge you bring into the electric field? You can do this the hard way, with formal definitions, or you can use the easy way. I prefer the easy way. Just think of electric field as coming from positive charges — that is, electric field arrows always do the following:

Point away from any positive charges that create the electric field

Go into negative charges

So you can always think of a bunch of positive charges as sitting at the base of the electric field arrows, and that tells you which way the force will act on the charge you bring into the electric field. For example, you have a negative charge in Figure 3-4, and you can think of the electric field arrows as coming from a bunch of positive charges — and because like charges repel, the force on your charge is away from the base of the arrows.

Looking at electric fields from charged objects

Not all electric fields are going to be as polite and evenly spaced as the electric field associated with the sheet of charge you see in Figure 3-4. For example, what’s the electric field from a point charge?

Say that you have a point charge Q and a small test charge q. How do you find the force per coulomb? Coulomb’s law to the rescue here — just plug in the charges Q and q (for q1 and q2) and the distance between them to get the size of the force (see the earlier section “Coulomb’s Law: Calculating the Force between Charges” for more on this formula):

So what’s the electric field? You know that E = F/q, so all you have to do is to divide by your test charge, q, to get the following:

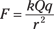
So the electric field at a given place falls off by a magnitude of r2, the square of the distance away from a point charge.

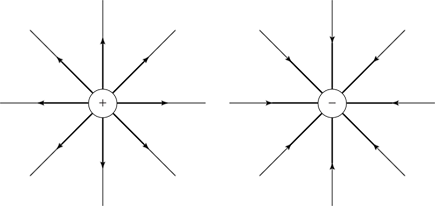
And what about the direction of the electric field? Well, the force exerted by a point charge is radial (that is, toward or away from the point charge). And electric field emanates from positive charges and goes into negative charges, so Figure 3-5 shows you what the electric field looks like for a positive point charge and a negative point charge.

Figure 3-5: The electric field from two point charges.

Uniform electric fields: Taking it easy with parallel plate capacitors

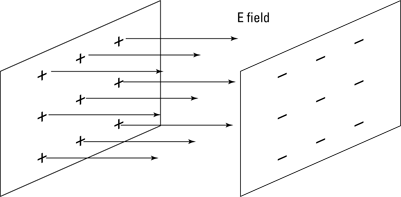
The electric field between multiple point charges isn’t the easiest thing to come to grips with in terms of vectors. So to make life easier, physicists came up with the parallel plate capacitor, which you see in Figure 3-6.

A parallel plate capacitor consists of two parallel conducting plates separated by a (usually small) distance. A charge +q is spread evenly over one plate and a charge –q is spread evenly over the other. That’s great for physicists’ purposes, because the electric field from all the point charges on these plates cancels out all components except the ones pointing between the plates, as you see in Figure 3-6.

Figure 3-6: The electric field between parallel charged plates.

So by being clever, physicists arrange to get a constant electric field, all in the same direction, which is a heck of a lot easier to work with than the field from point charges.

So what is the electric field between the plates? You can determine that the electric field (E) between the plates is constant (as long as the plates are close enough together), and in magnitude, it’s equal to

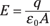
where εo, the so-called permittivity of free space, is 8.854 × 10–12 C2/(N-m2); q is the total charge on either of the plates (one plate has charge +q and the other is –q); and A is the area of each plate in square meters.

The equation for the electric field (E) between the plates of a parallel plate capacitor is often written in terms of the charge density, σ, on each plate, where σ = q/A (the charge per square meter), and here’s what that makes the equation look like:

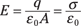
When you work with a parallel plate capacitor, life becomes a little easier because the electric field has a constant value and a constant direction (from the + plate to the – plate), so you don’t have to worry about where you are between those plates to find the electric field.

Take a look at an example. Say, for instance, that you put a positive charge of +1.0 coulombs inside the plates of a parallel plate capacitor, as in Figure 3-7.

Figure 3-7: A positive charge inside the electric field between parallel charged plates.

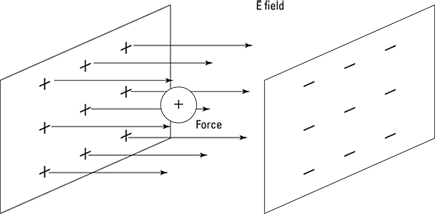
And also assume that the charge of the plates is 1.77 × 10–11 coulombs and that the area of each plate is 1.0 square meters. That would give you the following result for the electric field between the plates:

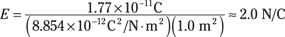
The electric field is a constant 2.0 newtons per coulomb. To find the force on a 1.0-coulomb charge, you know that

F = qE

And in this case, that’s 1.0 C × 2.0 N/C, for a total of 2.0 N (or about 0.45 pounds). That calculation is pretty simple, because the electric field between the parallel plates is constant — unlike what the electric field would be between two point charges.

Shielding: The electric field inside conductors

This section examines how, in any electric field at all, people can make a little safe haven — a region of zero electric field — with only the aid of a hollow conductor!

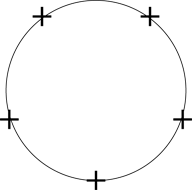
Figure 3-8 shows an internal cross-section of a spherical conducting ball. Say that some charges were planted inside the solid metal ball. Now, electric charges always generate an electric field, and conducting materials let charges flow freely in response to electric field, so what happens?

Figure 3-8: Charges inside a conductor.

The electric field generated by the charges implanted in the conducting material push other, similar charges away. As a result, charges move around until like charges are as far away from each other as possible. You can see the result in Figure 3-9 — charges immediately appear on the surface of the conductor. In fact, all the charge appears immediately on the surface — no net charge is left inside the conductor. (Note: Although this example shows positive charge moving, electrons really do the moving, so a reduction of electrons that appear on the surface is what creates a positive charge.)

Figure 3-9: Charges on the surface of a conductor.

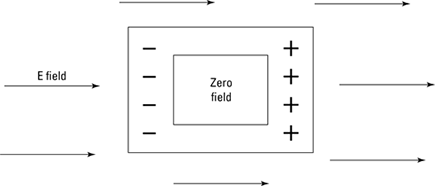
This kind of behavior — the free motion of charges in conductors — is very useful. For example, if you’re in the middle of a region of electric field and you want to have no electric field present, you can shield yourself from the electric field.

To shield yourself from the electric field, you place a conducting container in the field, as in Figure 3-10. The electric field outside the container induces a charge on the container. But the nature of conductors is to let charges flow if there’s any net charge — and any way for it to move around — so the electric field from the induced charges and the preexisting electric field cancel each other out. The result is that there’s no electric field inside the conducting container. You’ve shielded yourself from the external electric field. Nice.

Figure 3-10: Shielding yourself from an external electric field.

Voltage: Realizing Potential

This section discusses an electrical concept that’s surely familiar: the idea of voltage. Yes, the kind of voltage you get when you plug something into a wall socket. The kind you get when you put a battery into a flashlight or when you rely on a car battery to start your car.

Here, you see how voltage relates to electrical energy. As charges move in electric fields, they can swap some of their energy of motion (kinetic energy) for electrical energy, and vice versa. For example, if you have two opposite charges close together, you have to do some work to separate them due to their mutual attraction. After you’ve separated the two charges, the work you did doesn’t just disappear — it’s stored in the electrical potential energy between them. This section explains how this idea relates to voltage and how voltage relates to the electric field in the special cases of a uniform field and the field around a point charge.

Getting the lowdown on electric potential

If you have a mass in a gravitational field, it has potential energy. As you throw a ball upward, for example, the kinetic energy of its motion is converted to gravitational potential energy as it reaches its peak, and then the potential energy changes back to kinetic energy as the ball falls back to you. The gravitational forces on the ball do work and exchange potential and kinetic energy. Because a force likewise acts on charges in an electric field, you can speak about potential energy here, too. That potential energy is electric potential energy.

What makes all forms of energy essentially the same is that they can all be converted to mechanical work. As you may remember from Physics I, work done (W) is the result of a force (F) moving a body through a distance (s), and they’re related thus: W = Fs. The energy in the interaction of a charge with an electric field is converted to work when the electrical forces move the charge. Moving twice as much charge takes twice as much work for the electrical forces. The work that’s done for every unit of charge is the voltage.

In physics, voltage is called electric potential (not electric potential energy, which isn’t per unit of charge); sometimes, it’s just shortened to potential. Instead of using the term voltage, it’s more correct to say that electric potential is measured in volts, whose symbol is V.

Looking at lightning volts

In a thunderstorm, the clouds are at a different electric potential from the ground. The electric potential becomes too great for the air and the air breaks down, conducting electric charge, so every now and then, lightning strikes between the Earth and the clouds.

How many volts are between clouds and the Earth in a thunderstorm? Plenty. It takes 11,000 volts to make a spark across 1 centimeter of air — and there are 100,000 centimeters in a kilometer (about 0.62 miles), the typical height of a cloud during a thunderstorm. You do the math.

Okay, I’ll do the math: that’s 11,000 volts/centimeter × 100,000 centimeters = 1.1 × 109 volts — which is indeed plenty of volts when compared to, say, a wall socket that has 110 volts.

In the case of a gravitational field, the gravitational force moves a mass in the direction of lower potential — things fall to the ground because they have lower gravitational potential there. In the same way, electrical forces move charges in the direction of lower electrical potential. The faster that the potential energy drops in that direction, the greater the force.

Now remember that electric field is force per unit charge, and electric potential is potential energy per unit charge. Therefore, the electric field is directed down the gradient (slope) of the electrical potential and has a strength proportional to the steepness of the slope.

The electric potential (V) at a particular point in space is the electric potential energy of a test charge located at the point of interest divided by the magnitude of that test charge, like this:

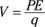
So you can think of electric potential as electric potential energy per coulomb.

So by how many volts does one plate of a charged parallel plate capacitor differ from the other plate? It differs by the energy needed to move 1 coulomb of charge from one plate to the other. (Note that volts are the same as joules/coulomb.)

Finding the work to move charges

Say that you’re sitting around, dismantling the smoke alarm in your apartment (which won’t make your landlord very happy) and you find a 9.0-volt battery. Whipping out the voltmeter you always carry, you measure the voltage between the terminals as exactly 9.0 volts. Hmm, you think. How much energy does it take to move one electron between the two terminals of the battery — a difference in electrical potential between the terminals of 9.0 volts?

Well, you realize that 9.0 volts is the change in potential energy per coulomb between the terminals. And change in potential energy is equal to work. So how much work does it take to move one electron between the terminals? You start by noting that the electric potential is

which means that

W = qΔV

Here, W is the work needed to move charge q across potential difference ΔV.

Now plug in some numbers. The charge of an electron is a miniscule –1.6 × 10–19 coulombs, and the potential difference between the negative and positive battery terminals is 9.0 volts, so

W = qΔV = (–1.6 × 10–19)(9.0) = –1.4 × 10–18 J

Therefore, –1.4 × 10–18 joules of work is done as the electron moves between the two terminals of a 9-volt battery.

You may remember the meaning of negative work from Physics I. The work is negative because the electron’s potential energy falls — that is, the electric force does the work of moving the electron. Moving the electron in the other direction would require an equal quantity of positive work from you, because you’d have to move it up the potential difference, against the electric field.

Finding the electric potential from charges

Say you have a point charge Q. What’s the electric potential due to Q at some distance r from the charge? You know that the size of the force on a test charge q due to the point charge is equal to the following (see the earlier section “Looking at electric fields from charged objects” for details):

where k is a constant equal to 8.99 × 109 N-m2/C2, Q is the point charge measured in coulombs, q is the charge of the test charge, and r is the distance between the point charge and the test charge.

You also know that the electric field at any point around a point charge Q is equal to the following:

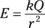
Thus, close to the point (when r is small), E is large and the field is therefore strong. As you move away from the point charge, r increases and the electric field quickly becomes weak.

Suppose you place a small test charge, q, in this field and try moving it around. The test charge feels a strong force close to the point charge, which quickly falls away as you move it to a greater distance. If the test charge is of the opposite sign to the point charge, you have to do work to pull it away from the point charge. This means that the test charge has a lower potential energy closer to the point charge (this is reversed if the charges are the same sign).

So what’s the electric potential from the point charge? At an infinite distance from the point charge, you can’t see it or be affected by it, so set the potential from the point charge to be zero there. As you bring a test charge closer, to a point r away from the point charge, you have to add up all the work you do and then divide by the size of the test charge. And the result after you do turns out to be gratifyingly simple. Here’s what that it looks like:

So the electrical potential is large close to the point charge (when r is small) and falls away at greater distances. This idea applies to all point charges, so what does it mean for the electrons orbiting the protons in an atom? How hard do you have to work to pull an electron away from an atom?

First find the electrical potential. The size of the charge of the electron and the proton is 1.6 × 10–19 coulombs. The electron and proton are typically 5.29 × 10–11 meters apart, so the electric potential is

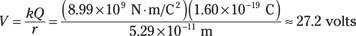
That close to the proton, the electric potential is a full 27.2 volts. That’s quite something for such a tiny charge!

The amount of energy needed to move an electron through 1 volt is called an electron-volt (eV). So you may expect that you’d need 27.2 eV of energy to pull an electron out of the atom. But the electron is moving quickly, so it already has some energy to contribute. In fact, the electron has so much kinetic energy that you need only half that, 13.6 eV of energy, to win the electron from the atom!

Illustrating equipotential surfaces for point charges and plates

To illustrate electric potential, you can draw equipotential surfaces; that is, surfaces that have the same potential at every point. Drawing an equipotential surface gives you an idea of what the electric potential from a charge or charge distribution looks like. For example, on one equipotential surface, the potential could always be 5.0 volts or 10.0 volts.

Because the potential from a point charge depends on the distance you are from the point charge, the equipotential surfaces for a point charge are a set of concentric spheres. You can see what they’d look like in Figure 3-11.

Figure 3-11: Dashed lines showing equipotential surfaces from a point charge.

Now consider equipotential surfaces between the plates of a parallel plate capacitor (see the earlier section “Uniform electric fields: Taking it easy with parallel plate capacitors” for more on these devices). If you start at the negatively charged plate and move a distance s toward the positively charged plate, you know that

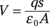
In other words, the equipotential surfaces here depend only on how far you are between the two plates. You can see this in Figure 3-12, which shows two equipotential surfaces between the plates of the parallel plate capacitor. Tip: This is analogous to the gravitational potential close to the ground, which increases in proportion to height. They’re both cases of uniform fields in which the field is the same at every point.

Figure 3-12: Equipotential surfaces between the plates of a parallel plate capacitor.

Storing Charge: Capacitors and Dielectrics

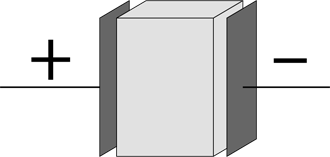
A capacitor, generally speaking, is something that stores charge. I discuss parallel plate capacitors earlier in this chapter, but a capacitor need not be shaped like two parallel plates — any two conductors separated by an insulator form a capacitor, regardless of shape. A dielectric increases how much charge a capacitor can hold. This section covers how capacitors and dielectrics work together.

Figuring out how much capacitors hold

How much charge is actually stored in a capacitor? That depends on its capacitance, C. The amount of charge stored in a capacitor is equal to its capacitance multiplied by the voltage across the capacitor:

q = CV

The MKS unit for capacitance C is coulombs per volt (C/V), also called the farad, F. For a parallel plate capacitor, the following is true (see the preceding section for details):

Because q = CV, you know that C = q/V, and you can solve the preceding equation to get the following:

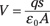
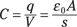
So that’s what the capacitance is for a parallel plate capacitor whose plates each have area A and are distance s apart.

Getting extra storage with dielectrics

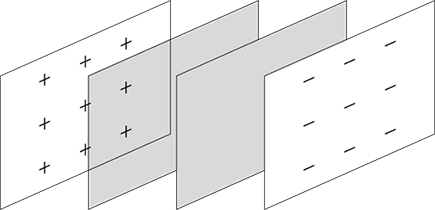
A dielectric is a semi-insulator that lets a capacitor store even more charge, and this substance works by reducing the electric field between the plates. Take a look at Figure 3-13. When you apply an electric field between the two plates, that induces some opposite charge on the dielectric, which opposes the applied electric field. The net result is that the electric field inside the dielectric (which fills the area between the plates) is reduced, allowing the capacitor to store more charge.

Figure 3-13: Using a dielectric between the plates of a parallel plate capacitor.

If you fill the space between the plates in a parallel plate capacitor with a dielectric, the capacitance of the parallel plate capacitor becomes the following:

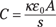
The dielectric increases the capacitance of the capacitor by the dielectric constant, κ, which differs for every dielectric. For example, the dielectric constant of mica, a commonly used mineral, is 5.4, so capacitors that use mica increase their capacitance by a factor of 5.4. The dielectric constant of a vacuum is 1.0.

Calculating the energy of capacitors with dielectrics

Because a capacitor stores charge, it can act as a source of electric current, like a battery. So in terms of capacitance and voltage, how much energy is stored in a capacitor?

Well, when you charge a capacitor, you assemble the final charge q in an average potential Vavg (you use the average potential because the potential increases as you add more charge). So here’s the energy stored:

Energy = qVavg

This raises the question, of course, of just what Vavg is. Because the voltage is proportional to the amount of charge on the capacitor (because q = CV), Vavg is one-half of the final charge. Or looked at another way, as you charge up a capacitor from 0 to its final voltage, the voltage increases linearly, so the average voltage is half the final voltage:

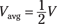
Plugging this value of Vavg into the energy equation and making the substitution that q = CV gives you the following equation:

For a parallel plate capacitor with a dielectric, the capacitance is

So the energy in a parallel plate capacitor with a dielectric in it is

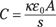
And there you have it — that’s the energy stored in a capacitor with a dielectric (the energy ends up in joules from this equation). You can see why dielectrics are considered a good idea when it comes to capacitors — they multiply the capacitance and the energy stored in a capacitor many-fold.