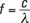Chapter 13
Understanding Energy and Matter as Both Particles and Waves
In This Chapter
Blackbody radiation
The photoelectric effect
Compton scattering
The de Broglie wavelength of matter
The Heisenberg uncertainty principle
What is matter? That’s a question that physicists have long been asking. And they’ve come up with some surprising answers. Everybody knows what electrons and protons are, right? They’re tiny particles that orbit around each other to form atoms, and they’re the fundamental building blocks of matter. But it turns out that the particle nature of electrons and protons and all matter isn’t quite right: Such particles can also act like waves. That sort of challenges the imagination — how can a baseball act as anything other than an object? How can matter act as a wave, a traveling disturbance that transfers energy? That’s the kind of question you look at in this chapter.
On the other hand, physicists have also been asking questions about light, which is known for its wave qualities. Chapter 11 covers how light works as a wave — for instance, how light passing through a pair of slits can interfere with itself and cause constructive and destructive interference. But light can show particle-like qualities, too — you’ve heard of photons, which are particles of light. So what is light? Waves or particles? The answer to that question is both: Light exhibits both particle and wave qualities, depending on what you’re measuring.
In this chapter, you look at the particle nature of light, the wave nature of electrons, and the experiments that suggested the relationships between energy and matter. All this ties in nicely with Einstein’s idea that mass and energy are equivalent, E = mc2, which I cover in Chapter 12. The result is a more complete picture of waves, particles, energy, and momentum. I start this chapter — as physicists started historically — by talking about the particle nature of light.
Blackbody Radiation: Discovering the Particle Nature of Light
The first experiment that showed how light could act like particles had to do with explaining the radiation spectrum of light that every object emits.
Blackbody radiation is the radiation from an ideal surface, which absorbs any wavelength of radiation incident upon it. Physicists studied blackbody radiation extensively by experiment and knew much about it by 1900, but little was understood until some quite revolutionary changes in physics. Not only did the problem of blackbody radiation suggest the particle nature of light, but it also led to the field of quantum physics. In this section, I explain the experimental results that hinted that light is more than just a wave.
Understanding the trouble with blackbody radiation
A glowing piece of charcoal, temperature about 1,000 kelvin, emits a cherry-colored light that you can see. And although people, who have a temperature of about 310 kelvin, don’t glow in the visible spectrum, they emit infrared light, which is visible to night scopes.
Physicists studied the spectrum of that light and found that it varied by the temperature of the object in question. Figure 13-1 shows the spectrum of emitted light — intensity versus wavelength — from a perfect blackbody (intensity is the amount of energy radiated by the wave per unit area per unit time, as I explain in Chapter 8). A perfect blackbody is simply an object, any object, that emits as much light as falls upon it from its environment.
The thing that puzzled physicists in the early part of the 20th century was the shape of the spectrum. As the temperature of the blackbody increased, the wavelength of the light emitted with the highest intensity decreased, creating a spectrum with the characteristic shape that you see in the figure. Physicists advanced plenty of theories as to just how a blackbody worked, but each theory was incomplete — at best, it could match only one part of the spectrum, at low wavelengths or at high wavelengths. But no one could give a satisfactory theoretical model of how blackbodies produced exactly the spectrum you see in Figure 13-1.
One attempt at an explanation of the blackbody spectrum only in terms of waves was made by Lord Rayleigh (John William Strutt, third Baron Rayleigh). His theory produced a prediction for the blackbody spectrum that fit quite well at large wavelengths; however, it had quite a serious problem — it predicted that a blackbody would radiate with infinite power! The predicted spectrum increased to infinity at shorter and shorter wavelengths. All attempts to explain the blackbody spectrum only with waves had similar problems.
Figure 13-1: The spectrum of blackbodies.
Being discrete with Planck’s constant
Max Planck, a German physicist, came along with a truly radical idea: He said that you have to consider the blackbody as a collection of many atomic oscillators, each of which emits radiation. The radical part of Planck’s idea was that such atomic-sized oscillators could only emit energies of
E = nhf n = 0, 1, 2, 3, ....
where n is a positive integer, f is the frequency of the oscillator, and h is a constant known as Planck’s constant:
h = 6.626 × 10–34 J ∙ s
That is, each atomic oscillator could only radiate energies that were discrete, that were multiples of hf. Other energies were not allowed. Today, when only certain energy states are allowed, you say that the system is quantized. That was the beginning of quantum physics. (You can find out more about quantum physics in my book Quantum Physics For Dummies [Wiley].)
The fact that energy could be emitted only with certain energies meant that not only were the atomic oscillators quantized but the emitted light was, too. In other words, light generated by a blackbody exists in discrete quanta, with only certain energies allowed. That contradicted the classical picture of light as a continuous spectrum of all possible wavelengths. Planck’s result implied the particle-like nature of light, with each particle of light having its own allowed energy.
Light Energy Packets: Advancing with the Photoelectric Effect
Albert Einstein was the one who first proposed that light consists of packets of energy. He did so as a result of his attempts to explain the so-called photoelectric effect, a phenomenon Heinrich Hertz first observed accidentally in 1887.
The photoelectric effect is called that because it relies on electrons that are ejected from a piece of metal by photons hitting that metal. This section describes the effect and how Einstein explained it.
Understanding the mystery of the photoelectric effect
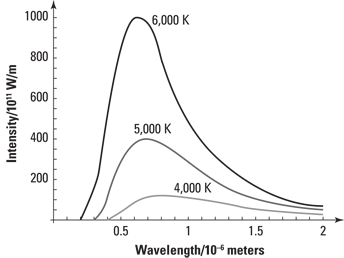
An experimental apparatus to measure the photoelectric effect appears in Figure 13-2. Here’s how it works: Electrons are normally trapped in the metal, attracted by the positive charge of the metal atoms’ nuclei. Even when a voltage is applied across the gap in the figure (between the metal sheet and the collector), the electrons are bound so tightly to the metal that they don’t leave the surface.
But when light shines on the sheet of metal, the light interacts with the atoms of metal, exciting them. Under certain circumstances, this light can cause electrons to break free from the surface of the metal. When the light gives the electrons the energy they need to leave the surface of the metal, they’re kicked out.
Those emitted electrons then travel to a positive plate, called the collector, as Figure 13-2 shows. The metal plate and collector are in a vacuum (inside a glass bell-jar or tube) to minimize the collisions of the electrons with the atoms of the air, which would complicate matters. Because the electrons travel from one metal plate to another, current flows (although a very small current), which can be measured by the meter at the bottom of the figure. So when you shine light onto the metal, current flows. It’s as simple as that.
To isolate the effect of the frequency of the incident light, researchers decided to shine monochromatic light (light of a particular frequency) on the metal plate. They could then study the effects of varying the frequency and intensity of this light separately.
Figure 13-2: The photoelectric effect.
Light would fall on the atoms of the metal, and physicists expected that when they used enough light waves, electrons would gather enough energy to be emitted. So classically, the more intensely the light shone on the metal, the more energy the emitted electrons should have. The assumption was that at very low levels of light, electrons would need some time to gather enough energy to be emitted. But that’s not what happened. Here are two surprising findings:
The energy of the emitted electrons turned out to be independent of the intensity of the light: If researchers doubled the amount of light, the electrons they saw didn’t end up with any different energy when they were emitted.
When researchers shone even low-intensity light on the metal, electrons started to be emitted immediately; it didn’t take time for them to gather enough energy before being emitted.
Einstein to the rescue: Introducing photons
Einstein, building on the work published by Max Planck (see the earlier section “Being discrete with Planck’s constant”), proposed that light was actually made up of discrete energy packets — today, you know those as photons. In particular, again following Planck, Einstein said that the energy of each photon is equal to
E = hf
where E is the energy of the photon, h is Planck’s constant (6.626 × 10–34 joule-seconds), and f is the frequency of the photon.
Calculating photons per second from a light bulb
Consider an electric light bulb of 100 watts. How many photons does it emit per second? Can you even think in terms of such a question? Yes, you certainly can. But you need to know the energy that the light emits every second and the energy of every photon. Because a light bulb’s spectrum more or less covers the visible spectrum, assume that the average visible wavelength of light from the bulb is green light (λ = 555 nanometers).
Okay, how much energy does the bulb emit per second? That’s 100 watts, which is 100 joules per second, right? Not exactly. Incandescent lights are only about 2 percent efficient — that is, a 100-watt bulb emits only 2 joules of visible light per second.
Okay, how many photons are in 2 joules per second? To determine that, you have to find the energy of each photon. You’re assuming the wavelength of the emitted light is green, on average λ = 555 nanometers. What’s the frequency? You can relate the speed of light (c) to its frequency (f) and wavelength (λ) like this:
So the frequency of green light is
That means the energy of one photon is
Ephoton = (6.626 × 10–34 J-s)(5.40 × 1014 Hz)
≈ 3.58 × 10–19 J
So the number of emitted photons per second is
So a 100-watt bulb emits about 6 × 1018 photons per second in the visible spectrum — a huge number.
Einstein’s equation shows that the energy of each photon depends on light frequency. For the photoelectric effect, Einstein suggested that each electron absorbs one photon, so the energy of the emitted electrons depends on light frequency as well. More-intense light contains more photons, so intensity can affect the number of electrons emitted but not the energy.
Now that you’re getting into photons, it’s worth asking what their mass is. After all, the whole point here is that photons act like particles. So do they have mass? From Chapter 11, you know that the energy of something in motion is
So rearrange the equation to isolate the mc2 term:
Now the (1 – v2/c2)1/2 term is zero, because by definition for photons, v = c. The energy is not zero, but the product of E times zero is zero, so mc2 = 0 — which means that m is zero. So the mass of photons is zero, nothing, nada.
Explaining why electrons’ kinetic energy is independent of intensity
So how exactly did Einstein use photons to explain the photoelectric effect? He had two issues to explain here: the idea that the kinetic energy of the emitted electrons is independent of the light intensity and the fact that electrons are emitted immediately, even in low-intensity light. I discuss kinetic energy in this section and the immediate release of electrons in the next.
Classically, you’d expect electrons to be emitted by electromagnetic waves with a continuous spectrum — and the more intense the light, the faster the ejected electrons should be going. But that’s not what happens. For a particular frequency of light, the ejected electrons have a particular kinetic energy — and even if you shine twice as much light on the metal, you don’t get electrons with more kinetic energy (you do get more electrons, however).
The particle theory of photons explains the photoelectric effect by saying that the energy of each photon — and therefore the energy it can deliver to a single electron — is dependent only on its frequency. So instead of having electrons absorb energy by being bathed in continuous light, each electron absorbs one photon.
That’s why the kinetic energy of the emitted electrons is independent of the light intensity: The intensity of the light determines only the number of photons, not their individual energy. It’s the photon energy that determines the kinetic energy of the ejected electrons.
According to Einstein’s photon model, each photon’s energy goes into
The energy needed to pull an electron out of the metal
The kinetic energy of that electron
The energy needed to pull electrons out of metal is called that metals’ work function, or WF, so the energy of each photon, which is hf, is equal to the following:
hf = KE + WF
where KE is the kinetic energy of the ejected electron and h is Planck’s constant (6.626 × 10–34 J-s).
This equation for the kinetic energy of the emitted electron tells the whole story: The kinetic energy of an emitted electron is just dependent on the frequency of the incoming photons, not their number, and the work function of the metal.
Explaining why electrons are emitted instantly
To describe the photoelectric effect, the second problem that Einstein had to solve was why electrons were emitted instantly when light — even low-intensity light — was shone on the metal.
Classically, you’d expect light intensity to have to build up enough energy to start ejecting electrons. But using Einstein’s energy-packet theory, you don’t need to wait until low-intensity light waves build up enough energy to emit electrons, because the light is actually made up of energy packets whose energy is dependent only on their frequency.
That means that as soon as you shine the light on the metal, you have photons that are energetic enough to eject electrons — no need to wait for the light to build up enough energy; each photon already has enough energy. Therefore, you still get electrons when you shine low-intensity light on metal; you just get fewer in number than when you shine more-intense light on the metal. Einstein triumphs again.
Doing calculations with the photoelectric effect
Take a look at an example. Say that as a good physicist, you practice the photoelectric effect on the first metal you come across, which happens to be Mom’s good set of silver spoons. When you shine your flashlight on the silver, do electrons pop out?
The work function of a metal is usually given in electron volts, eV, and 1 electron volt is the energy needed to move one electron through 1 volt of potential (you have to push the electron in order to do work on it, so you may think of this as pushing the electron toward the negatively charged plate of a parallel plate capacitor):
1 eV = 1.60 × 10–19 J
(That’s because work = qΔV, and q for an electron = 1.60 × 10–19 C, whereas ΔV = 1.0 V).
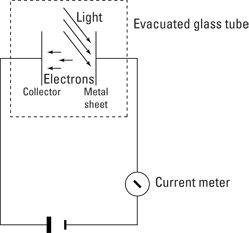
The work function of silver (WF) is 4.72 eV, so you need that many electron volts to free an electron from the silver. So what’s the frequency you need to start freeing electrons?
Converting 4.72 eV into joules gives you the energy needed to overcome the work function:
Eneeded = (4.72 eV)(1.60 × 10–19 J/eV) ≈ 7.55 × 10–19 J
Okay, so you need photons with an energy of 7.55 × 10–19 J. What frequency does that correspond to? You know that
Ephoton = hf
where h is Planck’s constant (6.626 × 10–34 joule-seconds) and f is the frequency of the photon. So you can rearrange the formula to say
Because the energy of the photon needs to be at least 7.55 × 10–19 J, you find that the minimum frequency needed is
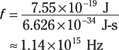
Okay, so the light you shine on Mom’s silver must have a frequency of at least 1.14 × 1015 hertz to eject electrons. What wavelength of light, λ, does that correspond to? Because c = λf, you know that
So the wavelength of light corresponding to the minimum frequency that you need is
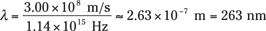
So the light must have a wavelength equal to or shorter than 263 nanometers — and that’s in the ultraviolet range, so your flashlight won’t work for the trick.
Collisions: Proving the Particle Nature of Light with the Compton Effect
Even though Einstein had announced that light travels in energy packets, the particle-like nature of light wasn’t fully accepted for several more years. What happened to change everybody’s mind? In 1923, physicist Arthur Compton performed an experiment in which he bounced photons off electrons, showing that both electrons and photons were scattered by the collision. And if that doesn’t prove the particle nature of photons, what would?
Compton sent beams of X-rays (that is, high-frequency photons) into targets made of graphite that had electrons at rest, just waiting to be hit. He observed that the photons were actually scattered by their collisions with electrons. He also noticed that the frequency of the scattered photons was lower than that of the incident photons, indicating that the photon had transferred some energy to the electron, which was initially at rest.
Not only do photons and electrons collide — they collide elastically, which means that both momentum and kinetic energy are conserved during the collision. In other words, the electron and photon bounce off each other in much the same way as billiard balls would. You can see a diagram of the scattering in Figure 13-3.
Energy is conserved when the electron is scattered by the photon. What’s that look like? That means that
Eincident photon = Escattered photon + KEscattered electron
Figure 13-3: The Compton effect.
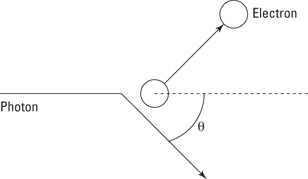
That is, the energy of the incident photon goes into the energy of the scattered photon and into the kinetic energy of the scattered electron (recall that the electron starts at rest). That’s half of the picture — the energy-conservation half. How about the momentum-conservation half of the picture?
For a colliding photon and electron, the momentum-conservation equation looks similar to the energy-conservation equation, except that here you’re dealing with momentum vectors, p, like this:
pincident photon = pscattered photon + pscattered electron
The momentum of a scattered electron is no problem — that’s mv, or the following in relativistic form (see Chapter 12 for details on special relativity and what happens at speeds near the speed of light):
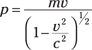
where p is the momentum of an object, m is the mass of the object, and v is the speed of the object.
So that’s okay for an electron. But what about the momentum for a photon, which doesn’t have any mass? Does that automatically mean that photons have no momentum? No, as the Compton effect demonstrates. The energy of a relativistic particle looks like this (also from Chapter 12):
This equation contains the mass of the particle, too. So are you stuck when trying to understand the energy and momentum of a photon, which has no mass? Not quite. You can divide the momentum by energy and have the mass drop out — and this works even for photons. So dividing the equation for momentum by the equation for energy, you get the following:
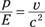
For photons, v = c so
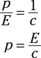
And for photons, E = hf, so
And you may notice that c = λf, so for a photon, the following is true:
Putting all this together, Compton was able to show that you can relate the wavelength of the incident and scattered photons like this:
where h is Planck’s constant (6.626 × 10–34 joule-seconds), m is the mass of the electron (9.11 × 10–31 kilograms), and θ is the scattering angle of the photon, as Figure 13-3 shows earlier in this section.
So the difference in wavelength between the incident photon and the scattered photon varies from zero if the photon continues on its way undeflected (θ = 0°) to h/mc if the photon is scattered through 90° (θ = 90°). In fact, the quantity h/mc comes up frequently in Compton scattering, so it’s called the Compton wavelength:
The Compton wavelength is equal to the following:
λCompton = 2.43 × 10–12 m
So using the Compton wavelength, the formula for Compton scattering gives you
λscattered photon – λincident photon = λCompton (1 – cos θ)
Compton scattering really put the issue to rest — photons can act as particles. The blackbody experiments (which I discuss earlier in “Blackbody Radiation: Discovering the Particle Nature of Light”) gave rise to the idea that light was quantized, and Einstein explained the photoelectric effect by saying light came in energy packets (see the earlier section “Light Energy Packets: Advancing with the Photoelectric Effect”), but what really hit the ball over the wall was the Compton effect.
The de Broglie Wavelength: Observing the Wave Nature of Matter
In 1924, a physics grad student, Louis de Broglie, came up with an incredibly bold suggestion: He proposed that physicists radically change their ideas of the nature of particles without any direct experimental grounds for doing so. Physicists had already discovered the particle aspects of light waves, but there was no evidence that compelled physicists to drastically alter their ideas of particles.
However, de Broglie felt nature would be more beautiful if there was a kind of symmetry whereby particles could also behave as waves. Because photons obey the following equation (which you see in the preceding section):
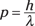
perhaps electrons and other particles would obey this equation:
That is, perhaps particles of matter have a wavelength, and it’s given by h/p. Amazingly, de Broglie turned out to be right. This section explains the experiments that supported this idea and then shows you how the math works.
Interfering electrons: Confirming de Broglie’s hypothesis
Experiments have borne out de Broglie’s idea. Early experiments were performed by bombarding nickel crystals with electrons and getting a diffraction pattern, just as you would from any wave. More recently, physicists sent electrons through a double-slit setup, producing the distinctive double-slit interference pattern (see Chapter 11 for info on light interference).
These physicists had a machine that emitted streams of electrons, and one day, they decided to pass the stream of electrons through a double-slit arrangement — the kind that gives rise to interference patterns with light waves. A funny thing happened on the way to the lecture hall: After adjusting the distance the double slits were apart, the same kind of interference pattern appeared — light and dark bars — on a photographic film (which records the positions at which the electrons strike it). The resulting light and dark bars looked exactly like an interference pattern, as Figure 13-4 shows.
Figure 13-4: The interference pattern of electrons sent through dual slits.
That was an amazing result for the time — a stream of electrons passing through a double slit and creating an interference pattern, just like light. The electrons were acting like waves, so the world had to come to grips with this new idea that electrons could act as waves or particles.
What this means is that physicists needed to change their mental picture of electrons. No longer could one comfortably think of electrons as small pool balls, orbiting around the nucleus of an atom. Instead, physicists had to think in terms of tiny wave-like packets of matter.
Calculating wavelengths of matter
De Broglie stated that the wavelength of an electron (λ) equals Planck’s constant (h = 6.626 × 10–34 joule-seconds) divided by momentum (p):
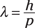
So do only electrons have a de Broglie wavelength? No, any object that has a momentum has a de Broglie wavelength, although the wavelength of objects you can see with the naked eye is vanishingly small. In this section, you calculate wavelengths of both electrons and larger objects.
Finding an electron’s de Broglie wavelength
Try some numbers to see how de Broglie’s wavelength works. For example, say you set an electron loose in your home and it starts zipping around at 1.9 × 106 meters per second. What’s its de Broglie wavelength? The electron’s speed is a nonrelativistic speed, far short of the speed of light in a vacuum, c, so the momentum of the electron is given by
p = mv
The mass of an electron is 9.11 × 10–31 kilograms, so the electron’s momentum is
p = (9.11 × 10–31 kg)(1.9 × 106 m/s) ≈ 1.74 × 10–24 kg-m/s
So the electron’s de Broglie wavelength is
That means the electron’s wavelength is 0.381 nanometers — about a thousand times smaller than the wavelength of visible light.
Finding the de Broglie wavelength of visible objects
Any object that has a momentum has a de Broglie wavelength. At about 0.381 nanometers, the de Broglie wavelength of the electron in the preceding section is huge compared to the de Broglie wavelength of an object visible to the naked eye.
Say that you’re determined to see the de Broglie wavelength for yourself, and you’ve decided to throw a baseball past a wavelength meter. You throw the baseball, mass 0.150 kilograms, at a hefty 90.0 miles per hour. What’s its de Broglie wavelength?
First, find out how fast the baseball is going in meters per second. As everybody knows, 1 meter per second is about 2.23693629 miles per hour. Okay, that’s a little ridiculous on the significant digits, but you find that 90.0 miles per hour equals the following:
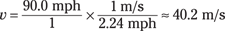
So the baseball’s momentum is
p = mv = (0.150 kg)(40.2 m/s) = 6.03 kg-m/s
Now you can figure out the de Broglie wavelength of the baseball using the equation:
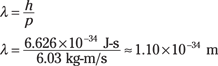
So the wavelength of the baseball is 1.10 × 10–34 meters, or 1.10 × 10–25 nanometers — an incredibly small distance. You cannot measure distances that small. I realize saying that is risky in a field as unpredictable as physics, but this wavelength is on the order of the Planck length.
Some theories about quantum gravity say that Planck length is the length at which the apparently continuous structure of the universe breaks down. At such a minute scale, quantum physics dominates, and what used to be measurements can be discussed only in terms of probabilities. So how small is the Planck length? It would take 100,000,000,000,000,000,000 (that is, 1020) Planck lengths to reach across a single proton. And that’s about the wavelength of a baseball going 90 miles per hour. Blows the mind, doesn’t it?
Not Too Sure about That: The Heisenberg Uncertainty Principle
You may have heard of the uncertainty principle — it’s one of those physics concepts that has gravitated to everyday speech, as in, “Where’s little Jimmy?” . . . “I don’t know — the closer you try to pin him down, the farther away he’ll be. You know, the uncertainty principle of children.”
You take a look at the actual uncertainty principle here, including a derivation of the equation from what you see in the preceding section on matter waves.
Understanding uncertainty in electron diffraction
Figure 13-5 shows a stream of electrons going through a single slit and creating a single-slit diffraction pattern on a screen (see Chapter 11 for more on single-slit diffraction patterns). In the days of Newton, you wouldn’t expect to see a diffraction pattern at all when you passed a stream of electrons through a single slit. You’d expect to see an exact image of the single slit on the screen (if you use photographic film as the screen, the pattern would be recorded on it).
Today, however, you know better. You know that you get a diffraction pattern — that is, a central bright bar surrounded by dark bars and lesser bright bars, as Figure 13-5 shows. Here’s the insight this brings: When you’re dealing with the small world (like electrons), you can no longer express things exactly.
For any individual electron going through the single slit, you can’t say exactly where it’s going to end up on the screen — it could end up anywhere there’s a bright bar in the diffraction pattern. You can’t assume that the electron will just keep going straight. You can speak of the electron’s location on the screen only in terms of probabilities — and as you send more and more electrons through the slit, you’ll end up with the diffraction pattern eventually.
Deriving the uncertainty relation
Say that the wavelength of the electrons passing through a single slit is λ and that the slit width is Δy, as in Figure 13-5. You can find the angle, θ, of the first dark bar in the diffraction pattern (as indicated in the figure) with the following equation:
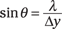
In other words, θ tells you the angular width of the central bright bar (where the electron will land about 85 percent of the time). And if θ is small, sin θ is about equal to tan θ (that is, for small angles, sin θ ≈ tan θ), so you have the following relation:
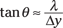
But what is the wavelength of the electron, λ? That’s where de Broglie comes in, because you know that for matter waves, the following is true (from the earlier section “The de Broglie Wavelength: Observing the Wave Nature of Matter”):
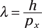
where px is the momentum of the electrons in the x direction and h is Planck’s constant (6.626 × 10–34 joule-seconds).
Figure 13-5: Single-slit diffraction for electrons.
Substituting this value for λ into the equation for tan θ gives you this result:
So far, so good. Now take a look at Figure 13-5. If the electrons enter the slit with momentum px, then after going through the slit, they acquire an unknown momentum of Δpy in the y direction (before the slit, you’re assuming the electrons’ momentum in the y direction was zero). Therefore, you have this relation between px and Δpy:
So setting the two equations for tan θ equal to each other gives you this result:
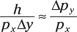
Multiplying both sides by px and solving for h leaves you with
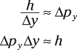
And actually, this is pretty close to the real Heisenberg uncertainty principle, which says that
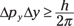
or in a more generic form:
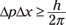
Where Δp and Δx are the uncertainty in momentum and position respectively, the Heisenberg uncertainty relation says that the uncertainty in an object’s momentum multiplied by the uncertainty in position must be greater than or equal to h/2π. In fact, h/2π is so common that it got its own name, 
(pronounced “h-bar”), so you often see Heisenberg’s uncertainty relation written like this:
where
(Planck’s constant divided by 2π)
Δp is the uncertainty in a particle’s momentum
Δx is the uncertainty in a particle’s position
Here’s how to think of the uncertainty relation for electrons passing through a single slit: By localizing the electrons to Δy (the slit), you introduce an uncertainty in the momentum Δpy such that 
.
As you can see from Heisenberg’s relation, the more accurately you know a particle’s momentum — that is, the smaller the uncertainty in momentum, Δp — the bigger the uncertainty in position, Δx. Conversely, the more accurately you know a particle’s position — that is, the smaller the uncertainty in position, Δx — the bigger the uncertainty in momentum, Δp.
As a matter of fact, the Heisenberg uncertainty principle can also connect the energy of a particle, E, with the time that particle has that energy, t, like this:
where
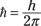(Planck’s constant divided by 2π)
ΔE is the uncertainty in a particle’s energy
Δt is the uncertainty in the time interval during which the particle is in this state
Calculations: Seeing the uncertainty principle in action
The Heisenberg uncertainty principle shows an inverse relationship: The more accurately you know the position of a particle, the less accurately you can know its momentum, and vice versa.
In this section, you plug in some numbers to see how pinpointing one measurement leads to less accuracy in the other.
Finding uncertainty in speed, given an electron’s position
Say that you use your new super-duper (and entirely theoretical) microscope to pin down the position of an electron to 1.00 × 10–11 meters. What’s the minimum uncertainty in the electron’s speed? Heisenberg tells you that
So the minimum uncertainty in the electron’s momentum is
Putting in the numbers gives you
What’s the uncertainty in speed? Well, for a nonrelativistic particle, p = mv, so
Therefore, the minimum uncertainty on speed is
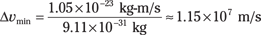
So if you know an electron’s position to within 1.0 × 10–11 meters of its actual location, you can only narrow its speed down to something within 1.15 × 107 meters per second of the actual speed — a mere 25,700,000 miles per hour.
That, of course, brings up the question of how you can measure anything about something moving at 25,700,000 miles per hour with respect to you, and the answer is that it’d be very difficult.
Finding uncertainty in position, given speed
Say that you want to hold an electron virtually still, at 1.00 × 10–5 meters per second — how closely can you localize it? At 1.00 × 10–5 meters per second, the electron’s momentum is
Δp = mΔv = (9.11 × 10–31 kg)(1.00 × 10–5 m/s)
≈ 9.11 × 10–36 kg-m/s
And you can find the minimum uncertainty on position, given an uncertainty in momentum, like this:
So if you pin down the speed of an electron to within 1.0 × 10–5 meters per second of the actual speed, you can’t locate it to less than 11.5 meters of its true location. Pretty slippery things, electrons!