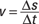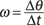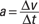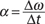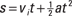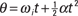Chapter 7
Circling around Rotational Motion and Orbits
In This Chapter
 Working with centripetal acceleration
Working with centripetal acceleration
 Feeling the pull of centripetal force
Feeling the pull of centripetal force
 Incorporating angular displacement, velocity, and acceleration
Incorporating angular displacement, velocity, and acceleration
 Orbiting with Newton’s laws and gravity
Orbiting with Newton’s laws and gravity
 Staying in the loop with vertical circular motion
Staying in the loop with vertical circular motion
Circular motion can include rockets’ moving around planets, race cars’ whizzing around a track, or bees’ buzzing around a hive. In this chapter, you look at the velocity and acceleration of objects that are moving in circles. This discussion leads to more general forms of rotational motion, where it’s useful to talk about motion in angular terms.
Angular equivalents exist for displacement, velocity, and acceleration. Instead of dealing with linear displacement as a distance, you deal with angular displacement as an angle. Angular velocity indicates what angle you sweep through in so many seconds, and angular acceleration gives you the rate of change in the angular velocity. All you have to do is take linear equations and substitute the angular equivalents: angular displacement for displacement, angular velocity for velocity, and angular acceleration for acceleration.
Centripetal Acceleration: Changing Direction to Move in a Circle
If the string holding the ball in Figure 7-1 breaks at the top, bottom, left, or right moment you see in the illustration, which way would the ball go? If the velocity points to the left, the ball would fly off to the left. If the velocity points to the right, the ball would fly off to the right. And so on. That’s not intuitive for many people, but it’s the kind of physics question that may come up in introductory courses.
Figure 7-1: Velocity constantly changes direction when an object is in circular motion.
Keeping a constant speed with uniform circular motion
An object with uniform circular motion travels in a circle with a constant speed. Practical examples may be hard to come by, unless you see a race car driver on a perfectly circular track with his accelerator stuck, a clock with a seconds hand that’s in constant motion, or the moon orbiting the Earth.
Take a look at Figure 7-2, where a golf ball tied to a string is whipping around in circles. The golf ball is traveling at a uniform speed as it moves around in a circle, so you can say it’s traveling in uniform circular motion.
Describing the period
Any object that travels in uniform circular motion always takes the same amount of time to move completely around the circle. That time is called its period, designated by T.
Figure 7-2: A golf ball on a string traveling with constant speed.
If you’re swinging a golf ball around on a string at a constant speed, you can easily relate the ball’s speed to its period. You know that the distance the ball must travel each time around the circle equals the circumference of the circle, which is 2πr (where r is the radius of the circle), so you can get the equation for finding an object’s period by first finding its speed:
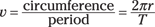
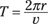
Say that you’re spinning a golf ball in a circle at the end of a 1.0-meter string every half-second. How fast is the ball moving? Time to plug in the numbers:
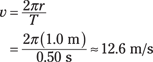
The ball moves at a speed of 12.6 meters/second. Just make sure you have a strong string!
Accelerating toward the center
When an object travels in uniform circular motion, its speed is constant, which means that the magnitude of the object’s velocity doesn’t change. Therefore, acceleration can have no component in the same direction as the velocity; if it did, the velocity’s magnitude would change.
However, the velocity’s direction is constantly changing — it always bends so that the object maintains movement in a constant circle. To make that happen, the object’s centripetal acceleration is always concentrated toward the center of the circle, perpendicular to the object’s velocity at any one time. The acceleration changes the direction of the object’s velocity while keeping the magnitude of the velocity constant.
In the ball’s case (refer to Figures 7-1 and 7-2), the string exerts a force on the ball to keep it going in a circle — a force that provides the ball’s centripetal acceleration. In order to provide that force, you have to constantly pull on the ball toward the center of the circle. (Picture what it feels like, force-wise, to whip an object around on a string.) You can see the centripetal acceleration vector, ac, in Figure 7-2.
If you accelerate the ball toward the center of the circle to provide the centripetal acceleration, why doesn’t it hit your hand? The answer is that the ball is already moving at a high speed. The force, and therefore the acceleration, that you provide always acts at right angles to the velocity.
Finding the magnitude of the centripetal acceleration
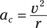
For a practical example, imagine you’re driving around curves at a high speed. For any constant speed, you can see from the equation ac = v2/r that the centripetal acceleration is inversely proportional to the radius of the curve. In other words, on tighter curves (as the radius decreases), your car needs to provide a greater centripetal acceleration (the acceleration increases).
Seeking the Center: Centripetal Force
When you’re driving a car around a bend, you create centripetal acceleration by the friction of your tires on the road. How do you know what force you need to create to turn the car at a given speed and turning radius? That depends on the centripetal force — the center-seeking, inward force needed to keep an object moving in uniform circular motion.
In this section, you discover how the centripetal force keeps the object moving in a circle and how the details of the circular motion such as radius and velocity depend upon the centripetal force.
Looking at the force you need
As you know from Newton’s first law (see Chapter 5), if there’s no net force on a moving object, the object will continue to move uniformly in a straight line. If a force (or a component of a force) acts in the same direction as the object’s velocity, then the object begins to speed up, and if the force acts in the opposite direction to the velocity, then the object slows down. However, if the force always acts perpendicularly to the velocity while remaining of constant magnitude, then the magnitude of the velocity (the speed) does not change; only its direction does — the object moves in a circle. In this case, the force is called centripetal force.
If you’re spinning a ball on a string, then the centripetal force comes from the tension in the string. When the moon orbits the Earth, the centripetal force comes from gravity. And when you drive your car in a circle, the centripetal force comes from the friction of the tires against the road. The origin of the force is not important, only that it remains of constant magnitude and always acts perpendicularly to the velocity, toward the center of the circle.
Seeing how the mass, velocity, and radius affect centripetal force
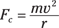
This equation tells you the magnitude of the force that you need to move an object of a given mass, m, in a circle at a given radius, r, and speed, v. (Remember that the direction of the force is always toward the center of the circle.)
Think about how force is affected if you change one of the other variables. The equation shows that if you increase mass or speed, you’ll need a larger force; if you decrease the radius, you’re dividing by a smaller number, so you’ll also need a larger force. Here’s how these ideas play out in the real world:
 Increasing mass: You may have an easy time swinging a golf ball on a string in a circle, but if you replace the golf ball with a cannonball, watch out. You may now have to whip 10 kilograms around on the end of a 1.0-meter string every half-second. As you can tell, you need a heck of a lot more force.
Increasing mass: You may have an easy time swinging a golf ball on a string in a circle, but if you replace the golf ball with a cannonball, watch out. You may now have to whip 10 kilograms around on the end of a 1.0-meter string every half-second. As you can tell, you need a heck of a lot more force.
 Increasing speed: Not interested in spinning cannonballs? Then imagine you’re driving your car around in a circle. If you’re going quite slowly around the circle, your tires have no problem generating enough frictional force to keep you going in the circle. But if you go too fast, then your tires can no longer generate the frictional force acting toward the center of the circle, so you start to skid.
Increasing speed: Not interested in spinning cannonballs? Then imagine you’re driving your car around in a circle. If you’re going quite slowly around the circle, your tires have no problem generating enough frictional force to keep you going in the circle. But if you go too fast, then your tires can no longer generate the frictional force acting toward the center of the circle, so you start to skid.
 Decreasing the radius: You can see the effect of the radius in your car going around in a circle. If you drive your car at a fixed speed in a circle of smaller and smaller radius, eventually your tires won’t be able to supply enough centripetal force from the friction, and you’ll skid off the circular path.
Decreasing the radius: You can see the effect of the radius in your car going around in a circle. If you drive your car at a fixed speed in a circle of smaller and smaller radius, eventually your tires won’t be able to supply enough centripetal force from the friction, and you’ll skid off the circular path.
Try plugging some numbers into the formula. The ball from Figure 7-2 is moving at 12.6 meters/second on a 1.0-meter string. How much force do you need to make a 10.0-kilogram cannonball move in the same circle at the same speed? Here’s what the equation looks like:

You need about 1,590 newtons, or about 357 pounds of force (4.448 newtons are in a pound; see Chapter 5). Pretty hefty, if you ask me; I just hope your arms can take it.
Negotiating flat curves and banked turns
Imagine that you’re driving a car and you come to a curve. On a flat road, the centripetal force you need to negotiate the curve comes from the friction of the tires against the ground. If the surface is covered with a substance such as ice, you have less friction, and you can’t turn as safely at high speeds.
To make turns safer, engineers design roads so that curves are banked. With the road at an angle, there’s a component of the normal force of the road against your car, toward the center of the circle. This means that you don’t require as much friction from your tires to make the turn.
Relying on friction to turn on a flat road
When you’re driving on a flat road, friction provides the centripetal force — toward the center of the circle — that allows you to make a turn.
Say you’re sitting in the passenger seat of the car, approaching a turn with a 200.0-meter radius (with a level, non-banked road surface). You know that the coefficient of static friction is 0.8 on this road (you use the coefficient of static friction because the tires aren’t slipping on the road’s surface) and that the car has a mass of about 1,000 kilograms. What’s the maximum speed the driver can go and still keep you safe? You get out your calculator as the driver shoots you a look with raised eyebrows. The frictional force needs to supply the centripetal force, so you come up with the following:
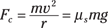
where m is the mass of the car, v is the velocity, r is the radius, μs is the coefficient of static friction, and g is the acceleration due to gravity, 9.8 meters/second2. Solving for the speed on one side of the equation gives you
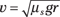
This looks simple enough — you just plug in the numbers to get
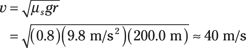
You calculate 40 meters/second, or about 87 miles/hour. You look at the speedometer and see a speed of 70 miles/hour. You can negotiate the turn safely at your present speed.
Depending on the normal force to make a banked turn
If a curve is banked, then a component of the normal force of the road against the car contributes to the centripetal force, and so you can go around the curve much faster. Because you don’t have to rely on friction to supply the centripetal force, the question of whether you can safely make the turn no longer depends on road conditions.
Take a look at Figure 7-3, which shows a car banking around a turn. The engineers can make the driving experience enjoyable if they bank the turn so that drivers garner the centripetal force needed to go around the turn entirely by the component of the normal force of the road against the car acting toward the center of the turn’s circle. That component is FN sin θ (FN is the normal force, the upward force perpendicular to the road; see Chapter 6), so
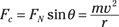
Figure 7-3: The forces acting on a car banking around a turn.
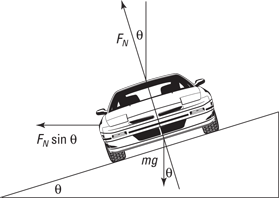
To find the centripetal force, you need the normal force, FN. If you look at Figure 7-3, you can see that FN comes from a combination of the centripetal force due to the car’s banking around the turn and the car’s weight. The purely vertical component of FN must equal mg, because no other forces are operating vertically, so
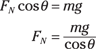
Plugging this result into the equation for centripetal force gives you
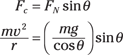
Because sin θ / cos θ = tan θ, you can also write this as
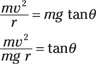
Solve for θ to find the angle of the road. The equation finally breaks down to
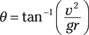
What should the angle θ be if drivers go around a 200-meter-radius turn at 60 miles/hour? Plug in the numbers; 60 miles/hour is about 27 meters/second and the radius of the turn is 200 meters, so
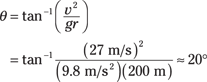
The designers should bank the turn at about 20° to give drivers a smooth experience. Remember though, that you made this calculation such that all the centripetal force comes from the normal force of the road against the car. You could go around the corner faster than this if you have some friction from your tires — but not too fast, or you’ll be skidding off into the verge!
Getting Angular with Displacement, Velocity, and Acceleration
For objects moving in a circle, you can work with acceleration and velocity using the horizontal and vertical components, just as in previous chapters on motion. But when objects are undergoing rotational motion, using angular variables instead makes a lot of sense. With these variables, instead of specifying the horizontal and vertical components, you specify the radius and the angle of rotation.
In this section, you discover the angular equivalents of displacement, velocity, and acceleration. You can apply these variables to rotating objects and objects moving in a circle.
Measuring angles in radians
The radian is a natural measure of angle because a circular arc that has a length of one radius extends an angle of 1 radian (see Figure 7-4). So if you know the radius and the angle that an object has moved through in radians, you can easily find the distance that the object has moved in proportion to the radius. If the object moves θ radians in a circle of radius r, then the object travels a distance of θr along the circle.
Figure 7-4: A circular arc extends an angle of one radian.
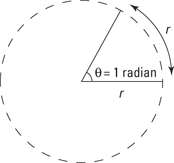
This idea is useful in relating the angular velocity to the speed of an object moving in a circle. In addition, you can see why a full circle has an angle of 2π radians: You know that the circumference of a circle is 2πr and that to go the whole way around the 360° of a circle, you need to travel 2π times the radius. Therefore, there are 2π radians to 360°.
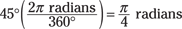
You find out that 45° = π/4 radians. If you have, say, π/2 radians and want to know how many degrees that converts to, you do this conversion:
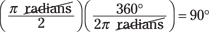
You calculate that π/2 radians = 90°.
Relating linear and angular motion
 Displacement: Instead of s, which you use in linear travel, use θ, the angular displacement; θ is measured in radians.
Displacement: Instead of s, which you use in linear travel, use θ, the angular displacement; θ is measured in radians.
 Velocity: In place of the velocity, v, use the angular velocity, ω; angular velocity is the number of radians covered per second.
Velocity: In place of the velocity, v, use the angular velocity, ω; angular velocity is the number of radians covered per second.
 Acceleration: Instead of acceleration, a, use the angular acceleration, α; the unit for angular acceleration is radians per second2.
Acceleration: Instead of acceleration, a, use the angular acceleration, α; the unit for angular acceleration is radians per second2.
Table 7-1 compares the formulas for both linear and angular motion.
Table 7-1 Linear and Angular Motion Formulas
|
Type of Formula |
Linear |
Angular |
|
Velocity |
|
|
|
Acceleration |
|
|
|
Displacement |
|
|
|
Motion with time canceled out |
vf2 – vi2 = 2as |
ωf2 – ωi2 = 2αθ |
Say, for example, that you have a ball tied to a string. What’s the angular velocity of the ball if you whirl it around? It makes a complete circle, 2π radians, in 0.5 seconds, so its angular velocity is
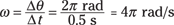
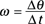
And multiply both sides by the radius, r, you get
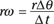
The term rΔθ is simply the distance traveled by an object moving in a circle of radius r, so this equation becomes
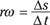
You may recognize the right side of this equation as the equation for speed. So you can see that linear speed and angular speed are related by rω = v.
If the ball speeds up from 4π radians per second to 8π radians per second in 2 seconds, what would its average angular acceleration be? Work it out by plugging in the numbers:
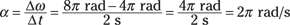
To find out more about angular displacement, angular velocity, and angular acceleration, see the discussion on angular momentum and torque in Chapter 11. Keep in mind, however, that these angular variables, like their linear counterparts, are actually vector quantities. What you’ve seen so far are simply components of vectors in one dimension. Because they only have one component, the sign of the component gives the direction in the single dimension (for example, positive indicates movement to the right, and negative indicates movement to the left). In Chapter 11, you see more about the direction and the vector nature of these variables.
Letting Gravity Supply Centripetal Force
You don’t have to tie objects to strings to observe travel in circular motion; larger bodies such as planets move in circular motion, too. Gravity provides the necessary centripetal force.
In this section, you discover Newton’s take on the gravitational force between two objects, and I show you how his theory relates to 9.8 meters/second2, the value experimenters identified as the acceleration due to gravity near the surface of the Earth. Then you put Newton’s formula to use in looking at the orbits of satellites.
Using Newton’s law of universal gravitation
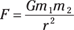
where G is a constant equal to 6.67 × 10–11 N·m2/kg2.
This equation allows you to figure the gravitational force between any two masses. What, for example, is the pull between the sun and the Earth? The sun has a mass of about 1.99 × 1030 kilograms, and the Earth has a mass of about 5.98 × 1024 kilograms. A distance of about 1.50 × 1011 meters separates the two bodies. Plugging the numbers into Newton’s equation gives you
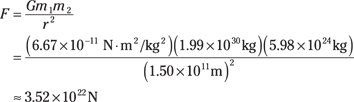
Your answer of 3.52 × 1022 newtons converts to about 8.0 × 1020 pounds of force (4.448 newtons are in a pound).
On the land-based end of the spectrum, say that you’re out for your daily physics observations when you notice two people on a park bench, looking at each other and smiling. As time goes on, you notice that they seem to be sitting closer and closer to each other each time you take a glance. In fact, after a while, they’re sitting right next to each other. What could be causing this attraction? If the two lovebirds have masses of about 75 kilograms each, what’s the force of gravity pulling them together, assuming they started out 0.50 meters away? Your calculation looks like this:
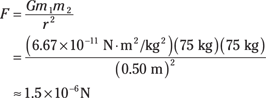
The force of attraction is roughly 5 millionths of an ounce. Maybe not enough to shake the surface of the Earth, but that’s okay. The Earth’s surface has its own forces to deal with.
Deriving the force of gravity on the Earth’s surface
The equation for the force of gravity — F = (Gm1m2)/r2 — holds true no matter how far apart two masses are. But you also come across a special gravitational case (which most of the work on gravity in this book is about): the force of gravity near the surface of the Earth.
The gravitational force between a mass and the Earth is the object’s weight. Mass is considered a measure of an object’s inertia, and its weight is the force exerted on the object in a gravitational field. On the surface of the Earth, the two forces are related by the acceleration due to gravity: Fg = mg. Kilograms and slugs are units of mass; newtons and pounds are units of weight.
You can use Newton’s law of gravitation to get the acceleration due to gravity, g, on the surface of the Earth just by knowing the gravitational constant G, the radius of the Earth, and the mass of the Earth. The force on an object of mass m1 near the surface of the Earth is
F = m1g
This force is provided by gravity between the object and the Earth, according to Newton’s gravity formula, and so you can write
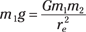
The radius of the Earth, re, is about 6.38 × 106 meters, and the mass of the Earth is 5.98 × 1024 kilograms. Putting in the numbers, you have
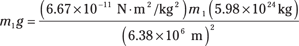
Dividing both sides by m1 gives you the acceleration due to gravity:
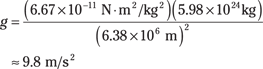
Newton’s law of gravitation gives you the acceleration due to gravity near the surface of the Earth: 9.8 meters/second2.
Of course, you can measure g by letting an apple drop and timing it, but what fun is that when you can calculate it in a roundabout way that requires you to first measure the mass of the Earth?
Using the law of gravitation to examine circular orbits
In space, bodies are constantly orbiting other bodies due to gravity. Satellites (including the moon) orbit the Earth, the Earth orbits the sun, the sun orbits around the center of the Milky Way, the Milky Way orbits around the center of its local group of galaxies. This is big-time stuff. In the case of orbital motion, gravity supplies the centripetal force that causes the orbits.
The force of gravity between orbiting bodies is quite a bit different from small-time orbital motion — such as when you have a ball on a string — because for a given distance and two masses, the gravitational force is always going to be the same. You can’t increase the force to increase the speed of an orbiting planet as you can with a ball. The following sections examine the speed and period of orbiting bodies in space.
Calculating a satellite’s speed
A particular satellite can have only one speed when in orbit around a particular body at a given distance because the force of gravity doesn’t change. So what’s that speed? You can calculate it with the equations for centripetal force and gravitational force. You know that for a satellite of a particular mass, m1, to orbit, you need a corresponding centripetal force (see the section “Seeking the Center: Centripetal Force”):
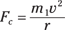
This centripetal force has to come from the force of gravity, so
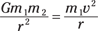
You can rearrange this equation to get the speed:
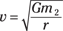
This equation represents the speed that a satellite at a given radius must have in order to orbit if the orbit is due to gravity. The speed can’t vary as long as the satellite has a constant orbital radius — that is, as long as it’s going around in circles. This equation holds for any orbiting object where the attraction is the force of gravity, whether it’s a human-made satellite orbiting the Earth or the Earth orbiting the sun. If you want to find the speed for satellites that orbit the Earth, for example, you use the mass of the Earth in the equation:
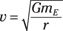
 You have to use the distance from the center of the Earth, not the distance above Earth’s surface, as the radius. Therefore, the distance you use in the equation is the distance between the two orbiting bodies. In this case, you add the distance from the center of the Earth to the surface of the Earth, 6.38 × 106 meters, to the satellite’s height above the Earth.
You have to use the distance from the center of the Earth, not the distance above Earth’s surface, as the radius. Therefore, the distance you use in the equation is the distance between the two orbiting bodies. In this case, you add the distance from the center of the Earth to the surface of the Earth, 6.38 × 106 meters, to the satellite’s height above the Earth.
 The equation assumes that the satellite is high enough off the ground that it orbits out of the atmosphere. That assumption isn’t really true for artificial satellites; even at 400 miles above the surface of the Earth, satellites do feel air friction. Gradually, the drag of friction brings them lower and lower, and when they hit the atmosphere, they burn up on re-entry. When a satellite is less than 100 miles above the surface, its orbit decays appreciably each time it circles the Earth. (Look out below!)
The equation assumes that the satellite is high enough off the ground that it orbits out of the atmosphere. That assumption isn’t really true for artificial satellites; even at 400 miles above the surface of the Earth, satellites do feel air friction. Gradually, the drag of friction brings them lower and lower, and when they hit the atmosphere, they burn up on re-entry. When a satellite is less than 100 miles above the surface, its orbit decays appreciably each time it circles the Earth. (Look out below!)
 The equation is independent of mass. If the moon rather than the artificial satellite orbited at 400 miles and you could ignore air friction and collisions with the Earth, it would have to go at the same speed as the satellite in order to preserve its close orbit (which would make for some pretty spectacular moonrises).
The equation is independent of mass. If the moon rather than the artificial satellite orbited at 400 miles and you could ignore air friction and collisions with the Earth, it would have to go at the same speed as the satellite in order to preserve its close orbit (which would make for some pretty spectacular moonrises).
Human-made satellites typically orbit at heights of 400 miles from the surface of the Earth (about 640 kilometers, or 6.4 × 105 meters). What’s the speed of such a satellite? All you have to do is put in the numbers:
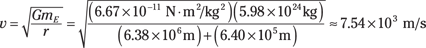
This converts to about 16,800 miles per hour.
Calculating the period of a satellite
Sometimes it’s more important to know the period of an orbit rather than the speed, such as when you’re counting on a satellite to come over the horizon before communication can take place. The period of a satellite is the time it takes it to make one full orbit around an object. The period of the Earth as it travels around the sun is one year.
If you know the satellite’s speed and the radius at which it orbits (see the preceding section), you can figure out its period. The satellite travels around the entire circumference of the circle — which is 2πr if r is the radius of the orbit — in the period, T. This means the orbital speed must be 2πr/T, giving you
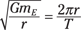
If you solve this for the period of the satellite, you get
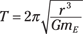
You, the intuitive physicist, may be wondering: What if you want to examine a satellite that simply stays stationary over the same place on the Earth at all times? In other words, a satellite whose period is the same as the Earth’s 24-hour period? Can you do it? Such satellites do exist. They’re very popular for communications, because they’re always orbiting in the same spot relative to the Earth; they don’t disappear over the horizon and then reappear later. They also allow for the satellite-based global positioning system, or GPS, to work.
In cases of stationary satellites, the period, T, is 24 hours, or about 86,400 seconds. Can you find the radius a stationary satellite needs to have? Using the equation for periods, you see that
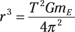
Plugging in the numbers, you get
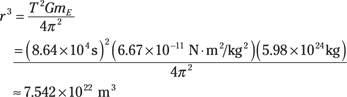
If you take the cube root of this, you get a radius of 4.23 × 107 meters. Subtracting the Earth’s radius of 6.38 × 106 meters, you get 3.59 × 107 meters, which converts to about 22,300 miles. This is the distance from the Earth geosynchronous satellites need to orbit. At this distance, they orbit the Earth at the same rate the Earth is turning, which means that they stay put over the same piece of real estate.
Looping the Loop: Vertical Circular Motion
Maybe you’ve watched extreme sports on television and wondered how bikers or skateboarders can ride into a loop on a track and go upside down without falling to the ground. Shouldn’t gravity bring them down? How fast do they have to go? The answers to these vertical circular-motion questions lie in centripetal force and the force of gravity.
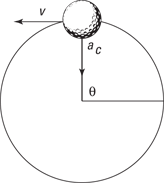
Take a look at Figure 7-5, where a ball is looping around a circular track. A question you may come across in introductory physics classes asks, “What speed is necessary so that the ball makes the loop safely?” The crucial point is at the very top of the track — if the ball is going to peel away from its circular track, the top is where it’ll fall. To answer the crucial question, you must know what criterion the ball must meet to hold on. Ask yourself, “What’s the constraint that the ball must meet?”
To travel in a loop, an object must have a net force acting on it that equals the centripetal force it needs to keep traveling in a circle of the given radius and speed. At the top of its path, as you can see in Figure 7-5, the ball barely stays in contact with the track. Other points along the track provide normal force (see Chapter 6) because of the speed and the fact that the track is curved. If you want to find out what minimum speed an object needs to have to stay on a loop, you need to look at where the object is just barely in contact with the track — in other words, on the verge of falling out of its circular path.
Figure 7-5: The force and velocity of a ball on a circular track.
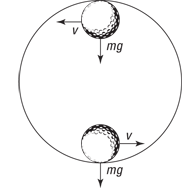
The normal force the track applies to an object at the top is just about zero. The only force keeping the object on its circular track is the force of gravity, which means that at the apex, the speed of the object has to be such that the centripetal force equals the object’s weight to keep it going in a circle whose radius is the same as the radius of the loop. That means that if this is the force needed
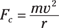
then the force of gravity at the top of the loop is
Fg = mg
And because Fg must equal Fc, you can write
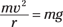
You can simplify this equation into the following form:
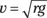
The mass of any object traveling around a circular track, such as a motorcycle or a race car, drops out of the equation.
The square root of r times g is the minimum speed an object needs at the top of the loop in order to keep going in a circle. Any object with a slower speed will peel off the track at the top of the loop (it may drop back into the loop, but it won’t be following the circular track at that point). For a practical example, if the loop from Figure 7-5 has a radius of 20.0 meters, how fast does the ball have to travel at the top of the loop in order to stay in contact with the track? Just put in the numbers:
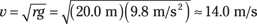
The golf ball has to travel 14.0 meters per second at the top of the track, which is about 31 miles per hour.
What if you want to do the same trick on a flaming circular loop on a motorcycle to impress your pals? The same speed applies — you need to be going about 31 miles per hour minimum at the top of the track, which has a radius of 20 meters. If you want to try this at home, don’t forget that this is the speed you need at the top of the track — you have to go faster at the bottom of the track in order to travel at 31 miles per hour at the top, simply because you’re twice the radius, or 40 meters, higher up in the air, much like having coasted to the top of a 40-meter hill.
So how much faster do you need to go at the bottom of the track? How about 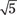 times faster? Check out Chapter 9, where kinetic energy (the kind of energy moving motorcycles have) is turned into potential energy (the kind of energy that motorcycles have when they’re high up in the air against the force of gravity).
times faster? Check out Chapter 9, where kinetic energy (the kind of energy moving motorcycles have) is turned into potential energy (the kind of energy that motorcycles have when they’re high up in the air against the force of gravity).