Chapter 9

Getting Some Work Out of Physics

In This Chapter

Taking stock of the work force

Evaluating kinetic and potential energy

Walking the path of conservative and nonconservative forces

Accounting for mechanical energy and power in work

You know all about work; it’s what you do when you have to do physics problems. You sit down with your calculator, you sweat a little, and you get through it. You’ve done your work. Unfortunately, that doesn’t count as work in physics terms.

In physics, work is done when a force moves an object through a displacement. That may not be your boss’s idea of work, but it gets the job done in physics. Along with the basics of work, I use this chapter to introduce kinetic and potential energy, look at conservative and nonconservative forces, and examine mechanical energy and power.

Looking for Work

Holding heavy objects — like, say, a set of exercise weights — up in the air seems to take a lot of work. In physics terms, however, that isn’t true. Even though holding up weights may take a lot of biological work, no mechanical work takes place if the weights aren’t moving.

In physics, mechanical work is performed on an object when a force moves the object through a displacement. When the force is constant and the angle between the force and the displacement is θ, then the work done is given by W = Fs cos θ. In layman’s terms, if you push a 1,000-pound hockey puck for some distance, physics says that the work you do is the component of the force you apply in the direction of travel multiplied by the distance you go.

To get a picture of the full work spectrum, you need to look across different systems of measurement. After you have the measurement units down, you can look at practical working examples, such as pushing and dragging. You can also figure out what negative work means.

Working on measurement systems

Work is a scalar, not a vector; therefore, it has only a magnitude, not a direction (more on scalars and vectors in Chapter 4). Because work is force times distance, Fs cos θ, it has the unit Newton-meter (N·m) in the MKS system (see Chapter 2 for info on systems of measurement).

Mechanical work done by a net force is equivalent to a transfer of energy (this is called the work-energy theorem), which has units called joules. Because of this, work and energy have the same units. For conversion purposes, 1 newton of force applied through a distance of 1 meter (where the force is applied along the line of the displacement) is equivalent to 1 joule, or 1 J, of work. (In the foot-pound-second system, work has the unit foot-pound. You can also discuss energy and work in terms of kilowatt-hours, which you may be familiar with from electric bills; 1 kilowatt-hour (kWh) = 3.6 × 106 joules.)

Pushing your weight: Applying force in the direction of movement

Motion is a requirement of work. For work to be done, a net force has to move an object through a displacement. Work is a product of force and displacement.

Here’s an example: Say that you’re pushing a huge gold ingot home, as Figure 9-1 shows. How much work do you have to do to get it home? To find work, you need to know both force and displacement. First, find out how much force pushing the ingot requires.

Figure 9-1: To do work on this gold ingot, you have to push with enough force to overcome friction and cause the ingot to move.

Suppose that the kinetic coefficient of friction (see Chapter 6), μk, between the ingot and the ground is 0.250 and that the ingot has a mass of 1,000 kilograms. What’s the force you have to exert to keep the ingot moving without accelerating it? Start with this equation for the force of friction:

FF = μk FN

Assuming that the road is flat, the magnitude of the normal force, FN, is just mg (mass times the acceleration due to gravity). That means that

FF = μk mg

where m is the mass of the ingot and g is the acceleration due to gravity on the surface of the Earth. Plugging in the numbers gives you the following:

FF = μk mg

= (0.250)(1,000 kg)(9.8 m/s2)

= 2,450 N

You have to apply a force of 2,450 newtons to keep the ingot moving without accelerating.

You know the force, so to find work, you need to know the displacement. Say that your house is 3 kilometers, or 3,000 meters, away. To get the ingot home, you have to do this much work:

W = Fs cos θ

Because you’re pushing the ingot with a force that’s parallel to the ground, the angle between F and s is 0°, and cos 0° = 1, so plugging in the numbers gives you the following:

W = Fs cos θ

= (2,450 N)(3,000 m)(1)

= 7.35 × 106 J

You need to do 7.35 × 106 joules of work to move your ingot home. Want some perspective? Well, to lift 1 kilogram 1 meter straight up, you have to supply a force of 9.8 newtons (about 2.2 pounds) over that distance, which takes 9.8 joules of work. To get your ingot home, you need 750,000 times that. Put another way, 1 kilocalorie equals 4,186 joules. A kilocalorie is commonly called a Calorie (capital C) in nutrition; therefore, to move the ingot home, you need to expend about 1,755 Calories. Time to get out the energy bars!

Using a tow rope: Applying force at an angle

You may prefer to drag objects rather than push them — dragging heavy objects may be easier, especially if you can use a tow rope, as Figure 9-2 shows.

When you’re pulling at an angle θ, you’re not applying a force in the exact same direction as the direction of motion. To find the work in this case, all you have to do is find the component of the force along the direction of travel. Work properly defined is the force along the direction of travel multiplied by the distance traveled:

W = Fpull s cos θ

Figure 9-2: More force is required to do the same amount of work if you pull at a larger angle.

Pulling harder to do the same amount of work

If you apply force at an angle instead of parallel to the direction of motion, you have to supply more force to perform the same amount of work.

Say that instead of pushing your ingot, you choose to drag it along with rope that’s at an angle of 10° from the ground instead of parallel. This time, θ = 10° instead of zero. If you want to do the same amount of work as when you pushed the ingot (7.35 × 106 joules), then you need the component of your force that is in the direction of the displacement to be the same as before — that is, 2,450 newtons. This means that

Fpull cos θ = 2,450 N

If you solve for the magnitude of your force, you have

If you pull at a 10° angle, you have to supply about 40 extra newtons of force to do the same amount of work. But before you brace yourself to pull really hard, think about the situation a bit more — you don’t have to do all that work.

Cutting down on your work by reducing friction

If you pull at an angle, the component of the force you apply that’s directed along the floor — in the direction of the displacement — does the work. The component of the force you apply that’s directed at right angles to this — straight up — does no work, but it does go some way toward lifting the ingot (or whatever you’re towing). The force isn’t big enough to lift the ingot clean off the ground, but it does reduce its normal force with the ground, and you know what that means: less friction.

Work out how much frictional force you have if you drag your ingot with a rope that’s at a 10° angle. The coefficient of friction is the same as before, but now the normal force with the ground is given by the weight of the ingot minus the upward component of the force you supply. Therefore, the force of friction is given by

Ffriction = μ(mg – Fpull sin θ)

Here, the vertical component of the force you apply to the ingot is given by Fpull sin θ. The force of friction must be smaller than before because the normal force is smaller — you can already see that you need to do less work to move the ingot.

Because you want to do the least amount of work, you want to drag the ingot across the ground with the smallest force needed to overcome friction. So set the horizontal component of your force equal to the force of friction:

Fpull cos θ = Ffriction

Now plug in the frictional force, which gives you the following:

Fpull cos θ = μ(mg – Fpull sin θ)

If you rearrange this equation to solve for Fpull, you can find the magnitude of the force you need to apply:

This is slightly smaller than the force you’d have to apply if you pushed the ingot straight on. If the rope is at a 10° angle, the work you’d do in pulling the ingot over the horizontal distance of 3,000 meters would be

W = Fpull s cos θ

= (2,380 N)(3,000 m)(cos 10°)

≈ 7.0 × 106 J

So you see, you have to do less work if you pull at an angle because there’s less frictional force to overcome.

Negative work: Applying force opposite the direction of motion

If the force moving the object has a component in the same direction as the motion, the work that force does on the object is positive. If the force moving the object has a component in the opposite direction of the motion, the work done by that force on the object is negative.

Consider this example: You’ve just gone out and bought the biggest television your house can handle. You finally get the TV home, and you have to lift it up the porch stairs. It’s a heavy one — about 100 kilograms, or 220 pounds — and as you lift it up the first few stairs, a distance of about 0.50 meters, you think you should’ve gotten some help because of how much work you’re doing (Note: F equals mass times acceleration, or 100 kilograms times g, the acceleration due to gravity; θ is 0° because the force and the displacement are in the same direction, the direction in which the TV is moving.):

W1 = Fs cos θ

= mgs cos 0°

= (100 kg)(9.8 m/s2)(0.50 m)(1.0) = 490 J

However, as you get the TV to the top of the steps, your back decides that you’re carrying too much weight and advises you to drop it. Slowly, you lower the TV back to its original position (with no acceleration so that the force you apply is equal and opposite to the weight of the TV) and take a breather. How much work did you do on the way down? Believe it or not, you did negative work on the TV, because the force you applied (still upward) was in the opposite direction of travel (downward). In this case, θ = 180°, and cos 180° = –1. Here’s what you get when you solve for the work:

W2 = Fs cos θ

= mgs cos 180°

= (100 kg)(9.8 m/s2)(0.50 m)(–1.0) = –490 J

The net work you’ve done is W = W1 + W2 = 0 joules, or zero work. That makes sense, because the TV is right back where it started.

Because the force of friction always acts to oppose the motion, the work done by frictional forces is always negative.

Making a Move: Kinetic Energy

When you start pushing or pulling a stationary object with a constant force, it starts to move if the force you exert is greater than the net forces resisting the movement, such as friction and gravity. If the object starts to move at some speed, it will acquire kinetic energy. Kinetic energy is the energy an object has because of its motion. Energy is the ability to do work.

You know the ins and outs of kinetic energy. So how do you calculate it?

The work-energy theorem: Turning work into kinetic energy

A force acting on an object that undergoes a displacement does work on the object. If this force is a net force that accelerates the object (according to Newton’s second law — see Chapter 5), then the velocity changes due to the acceleration (see Chapter 3). The change in velocity means that there is a change in the kinetic energy of the object.

The change in kinetic energy of the object is equal to the work done by the net force acting on it. This is a very important principle called the work-energy theorem.

After you know how work relates to kinetic energy, you’re ready to take a look at how kinetic energy relates to the speed and mass of the object.

The equation to find kinetic energy, KE, is the following, where m is mass and v is velocity:

Using a little math, you can show that work is also equal to (1/2)mv2. Say, for example, that you apply a force to a model airplane in order to get it flying and that the plane is accelerating. Here’s the equation for net force:

F = ma

The work done on the plane, which becomes its kinetic energy, equals the following:

W = Fs cos θ

Net force, F, equals mass times acceleration. Assume that you’re pushing in the same direction that the plane is going; in this case, cos 0° = 1, so

W = Fs = mas

You can tie this equation to the final and original velocity of the object. Use the equation vf2 – vi2 = 2as (see Chapter 3), where vf equals final velocity and vi equals initial velocity. Solving for a gives you

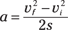
If you plug this value of a into the equation for work, W = mas, you get the following:

If the initial velocity is zero, you get

This is the work that you put into accelerating the model plane — that is, into the plane’s motion — and that work becomes the plane’s kinetic energy, KE:

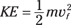
This is just the work-energy theorem stated as an equation.

Using the kinetic energy equation

You normally use the kinetic energy equation to find the kinetic energy of an object when you know its mass and velocity. Say, for example, that you’re at a firing range and you fire a 10-gram bullet with a velocity of 600 meters/second at a target. What’s the bullet’s kinetic energy? The equation to find kinetic energy is

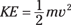
All you have to do is plug in the numbers, remembering to convert from grams to kilograms first to keep the system of units consistent throughout the equation:

The bullet has 1,800 joules of energy, which is a lot of energy to pack into a 10-gram bullet.

You can also use the kinetic energy equation if you know how much work goes into accelerating an object and you want to find, say, its final speed. For example, say you’re on a space station, and you have a big contract from NASA to place satellites in orbit. You open the station’s bay doors and grab your first satellite, which has a mass of 1,000 kilograms. With a tremendous effort, you hurl it into its orbit, using a net force of 2,000 newtons, applied in the direction of motion, over 1 meter. What speed does the satellite attain relative to the space station? The work you do is equal to

W = Fs cos θ

Because θ = 0° here (you’re pushing the satellite straight on), W = Fs:

W = Fs = (2,000 N)(1.0 m) = 2,000 J

Your work goes into the kinetic energy of the satellite, so

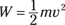
Now solve for v and plug in some numbers. You know that m equals 1,000 kilograms and W equals 2,000 joules, so

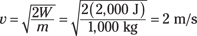
The satellite ends up with a speed of 2 meters/second relative to you — enough to get it away from the space station and into its own orbit.

Bear in mind that forces can also do negative work. If you want to catch a satellite and slow it to 1 meter/second with respect to you, the force you apply to the satellite is in the opposite direction of its motion. That means it loses kinetic energy, so you do negative work on it.

Calculating changes in kinetic energy by using net force

In everyday life, multiple forces act on an object, and you have to take them into account. If you want to find the change in an object’s kinetic energy, you have to consider only the work done by the net force. In other words, you convert only the work done by the net force into kinetic energy.

For example, when you play tug-of-war against your equally strong friends, you pull against each other but nothing moves. Because there’s no movement, no work is done and you have no net increase in kinetic energy from the two forces.

Take a look at Figure 9-3. You may want to determine the speed of the 100-kilogram refrigerator at the bottom of the ramp, using the fact that the net work done on the refrigerator goes into its kinetic energy. How do you do that? You start by determining the net force on the refrigerator and then find out how much work that force does. Converting that net-force work into kinetic energy lets you calculate what the refrigerator’s speed will be at the bottom of the ramp.

Figure 9-3: You find the net force acting on an object to find its speed at the bottom of a ramp.

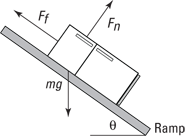
What’s the net force acting on the refrigerator? In Chapter 6, you find that the component of the refrigerator’s weight acting along the ramp is

Fg, ramp = mg sin θ

where m is the mass of the refrigerator and g is the acceleration due to gravity. The normal force is

FN = mg cos θ

which means that the kinetic force of friction is

FF = μk FN = μk mg cos θ

where μk is the kinetic coefficient of friction. The net force accelerating the refrigerator down the ramp, Fnet, therefore, is

Fnet = Fg, ramp – FF = mg sin θ – μk mg cos θ

You’re most of the way there! If the ramp is at a 30° angle to the ground and there’s a kinetic coefficient of friction of 0.57, plugging the numbers into this equation results in the following:

Fnet = (100 kg)(9.8 m/s2)(sin 30°) – (0.57)(100 kg)(9.8 m/s2)(cos 30°) ≈ 6.2 N

The net force acting on the refrigerator is about 6.2 newtons. This net force acts over the entire 3.0-meter ramp, so the work done by this force is

W = Fnets

= (6.2 N)(3.0 m) ≈ 19 J

You find that 19 joules of work goes into the refrigerator’s kinetic energy. That means you can find the refrigerator’s kinetic energy like this:

You want the speed here, so solving for v and plugging in the numbers gives you

The refrigerator will be going 0.61 meters/second at the bottom of the ramp.

Energy in the Bank: Potential Energy

There’s more to motion than kinetic energy — an object can also have potential energy, which is stored energy or the energy an object has because of its position. The energy is called potential because it can be converted to kinetic energy or other forms of energy, such as heat.

Objects can have potential energy from different sources. To give an object potential energy, all you need to do is perform work on an object against a force, such as when you pull back on an object connected to a spring. Gravity is a very common source of potential energy in physics problems.

Suppose you have the job of taking your little cousin Jackie to the park, and you put the little tyke on the slide. Jackie starts at rest and then accelerates, ending up with quite a bit of speed at the bottom of the slide. You sense physics at work here. Taking out your clipboard, you put Jackie higher up the slide and let go, watching carefully. Sure enough, Jackie ends up going even faster at the bottom of the slide. You decide to move Jackie even higher up. (Suddenly, Jackie’s mother shows up and grabs him from you. That’s enough physics for one day.)

What was happening on the slide? Where did Jackie’s kinetic energy come from? It ultimately came from the work you did lifting Jackie against the force of gravity. Jackie sits at rest at the bottom of the slide, so he has no kinetic energy. If you lift him to the top of the slide and hold him, he waits for the next trip down the slide, so he has no motion and no kinetic energy. However, you did work lifting him up against the force of gravity, so he has potential energy. As Jackie slides down the (frictionless) slide, gravity turns your work — and Jackie’s potential energy — into kinetic energy.

To new heights: Gaining potential energy by working against gravity

How much work do you do when you lift an object against the force of gravity? Suppose that you want to store a cannonball on an upper shelf at height h above where the cannonball is now. The work you do is

W = Fs cos θ

In this case, F equals the force required to overcome gravity, s equals distance, and θ is the angle between them. The gravitational force on an object is mg (mass times the acceleration due to gravity, 9.8 meters/second2), and when you lift the cannonball straight up, θ = 0°, so

W = Fs cos θ = mgh

The variable h here is the distance you lift the cannonball. To lift the ball, you have to do a certain amount of work, or m times g times h. The cannonball is stationary when you put it on the shelf, so it has no kinetic energy. However, it does have potential energy, which is the work you put into the ball to lift it to its present position.

If the cannonball rolls to the edge of the shelf and falls off, how much kinetic energy would it have just before it strikes the ground (which is where it started when you first lifted it)? It would have mgh joules of kinetic energy at that point. The ball’s potential energy, which came from the work you put in lifting it, changes to kinetic energy thanks to the fall.

In general, you can say that if you have an object of mass m near the surface of the Earth (where the acceleration due to gravity is g), at a height h, then the potential energy of that mass compared to what it’d be at height 0 (where h = 0 at some reference height) is

PE = mgh

And if you move an object vertically against the force of gravity from height hi to height hf, its change in potential energy is

ΔPE = mg(hf – hi)

The work you perform on the object changes its potential energy.

Achieving your potential: Converting potential energy into kinetic energy

Gravitational potential energy for a mass m at height h near the surface of the Earth is mgh more than the potential energy would be at height 0. (It’s up to you where you choose height 0.)

For example, say that you lift a 40-kilogram cannonball onto a shelf 3.0 meters from the floor, and the ball rolls and slips off, headed toward your toes. If you know the potential energy involved, you can figure out how fast the ball will be going when it reaches the tips of your shoes. Resting on the shelf, the cannonball has this much potential energy with respect to the floor:

PE = mgh

= (40 kg)(9.8 m/s2)(3.0 m)

≈ 1,200 J

The cannonball has 1,200 joules of potential energy stored by virtue of its position in a gravitational field. What happens when it drops, just before it touches your toes? That potential energy is converted into kinetic energy. So how fast will the cannonball be going at toe impact? Because its potential energy is converted into kinetic energy, you can write the problem as the following (see the section “Making a Move: Kinetic Energy” earlier in this chapter for an explanation of the kinetic energy equation):

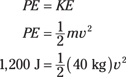
Plugging in the numbers and putting velocity on one side, you get the speed:

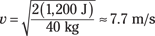
The velocity of 7.7 meters/second converts to about 25 feet/second. You have a 40-kilogram cannonball — or about 88 pounds — dropping onto your toes at 25 feet/second. You play around with the numbers and decide you don’t like the results. Prudently, you turn off your calculator and move your feet out of the way.

Choose Your Path: Conservative versus Nonconservative Forces

The work a conservative force does on an object is path-independent; the actual path taken by the object makes no difference. Fifty meters up in the air has the same gravitational potential energy whether you get there by taking the steps or by hopping on a Ferris wheel. That’s different from the force of friction, which dissipates kinetic energy as heat. When friction is involved, the path you take does matter — a longer path will dissipate more kinetic energy than a short one. For that reason, friction is a nonconservative force.

For example, suppose you and some buddies arrive at Mt. Newton, a majestic peak that rises h meters into the air. You can take two ways up — the quick way or the scenic route. Your friends drive up the quick route, and you drive up the scenic way, taking time out to have a picnic and to solve a few physics problems. They greet you at the top by saying, “Guess what — our potential energy compared to before is mgh greater.”

“Mine, too,” you say, looking out over the view. You pull out this equation (originally presented in the section “To new heights: Gaining potential energy by working against gravity,” earlier in this chapter):

ΔPE = mg(hf – hi)

This equation basically states that the actual path you take when going vertically from hi to hf doesn’t matter. All that matters is your beginning height compared to your ending height. Because the path taken by the object against gravity doesn’t matter, gravity is a conservative force.

Here’s another way of looking at conservative and nonconservative forces. Say that you’re vacationing in the Alps and that your hotel is at the top of Mt. Newton. You spend the whole day driving around — down to a lake one minute, to the top of a higher peak the next. At the end of the day, you end up back at the same location: your hotel on top of Mt. Newton.

What’s the change in your gravitational potential energy? In other words, how much net work did gravity perform on you during the day? Gravity is a conservative force, so the change in your gravitational potential energy is 0. Because you’ve experienced no net change in your gravitational potential energy, gravity did no net work on you during the day.

The road exerted a normal force on your car as you drove around (see Chapter 6), but that force was always perpendicular to the road, so it didn’t do any work, either.

Conservative forces are easier to work with in physics because they don’t “leak” energy as you move around a path — if you end up in the same place, you have the same amount of energy. If you have to deal with nonconservative forces such as friction, including air friction, the situation is different. If you’re dragging something over a field carpeted with sandpaper, for example, the force of friction does different amounts of work on you depending on your path. A path that’s twice as long will involve twice as much work to overcome friction.

What’s really not being conserved around a track with friction is the total potential and kinetic energy, which taken together is mechanical energy. When friction is involved, the loss in mechanical energy goes into heat energy. You can say that the total amount of energy doesn’t change if you include that heat energy. However, the heat energy dissipates into the environment quickly, so it isn’t recoverable or convertible. For that and other reasons, physicists often work in terms of mechanical energy.

Keeping the Energy Up: The Conservation of Mechanical Energy

Mechanical energy is the sum of potential and kinetic energy, or the energy acquired by an object upon which work is done. The conservation of mechanical energy, which occurs in the absence of nonconservative forces (see the preceding section), makes your life much easier when solving physics problems, because the sum of kinetic energy and potential energy stays the same.

In this section, you examine the different forms of mechanical energy: kinetic and potential. You also find out how to relate the kinetic energy to the object’s motion, how potential energy arises from the forces acting on the object, and how you can calculate the potential energy for the particular case of gravitational forces. And last, I explain how you can use mechanical energy to make calculations easier.

Shifting between kinetic and potential energy

Imagine a roller coaster car traveling along a straight stretch of track. The car has mechanical energy because of its motion: kinetic energy. Imagine that the track has a hill and that the car has just enough energy to get to the top before it descends the other side, back down to a straight and level track (see Figure 9-4). What happens? Well, at the top of the hill, the car is pretty much stationary, so where has all its kinetic energy gone? The answer is that it has been converted to potential energy. As the car begins its descent on the other side of the hill, the potential energy begins to be converted back to kinetic energy, and the car gathers speed until it reaches the bottom of the hill. Back at the bottom, all the potential energy the car had at the top of the hill has been converted back into kinetic energy.

An object’s potential energy derives from work done by forces, and a label for a particular potential energy comes from the forces that are its source. For example, the roller coaster has potential energy because of the gravitational forces acting on it, so this is often called gravitational potential energy. For more on potential energy, see the section “Energy in the Bank: Potential Energy” earlier in this chapter.

Figure 9-4: Kinetic energy converted to potential energy and then back to kinetic energy.

The roller coaster car’s total mechanical energy, which is the sum of its kinetic and potential energies, remains constant at all points of the track. The combination of the kinetic and potential energies does vary, however. When no work is done on an object, its mechanical energy remains constant, whatever motions it may undergo.

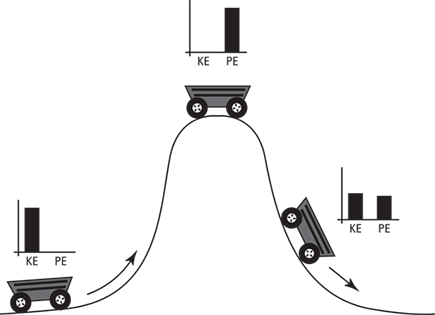
Say, for example, that you see a roller coaster at two different points on a track — Point 1 and Point 2 — so that the coaster is at two different heights and two different speeds at those points. Because mechanical energy is the sum of the potential energy (mass × gravity × height) and kinetic energy (1⁄2 mass × velocity2), the total mechanical energy at Point 1 is

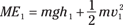
At Point 2, the total mechanical energy is

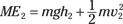
What’s the difference between ME2 and ME1? If there’s no friction (or another nonconservative force), then ME1 = ME2, or

These equations represent the principle of conservation of mechanical energy. The principle says that if the net work done by nonconservative forces is zero, the total mechanical energy of an object is conserved; that is, it doesn’t change. (If, on the other hand, friction or another nonconservative force is present, the difference between ME2 and ME1 is equal to the net work the nonconservative forces do: ME2 – ME1 = Wnc.

Another way of rattling off the principle of conservation of mechanical energy is that at Point 1 and Point 2,

PE1 + KE1 = PE2 + KE2

You can simplify that mouthful to the following:

ME1 = ME2

where ME is the total mechanical energy at any one point. In other words, an object always has the same amount of energy as long as the net work done by nonconservative forces is zero.

You can cancel out the mass, m, in the previous equation, which means that if you know three of the values (heights and velocities), you can solve for the fourth:

The mechanical-energy balance: Finding velocity and height

Breaking apart the equation for mechanical energy into potential and kinetic energy at two different points — gh1 + (1/2)v12 = gh2 + (1/2)v22 — allows you to solve for individual variables, such as velocity and height. Check out the following examples.

Determining final velocity with mechanical energy

You can use the principle of conservation of mechanical energy to find an object’s final speed.

“Serving as a roller coaster test pilot is a tough gig,” you say as you strap yourself into the Physics Park’s new Bullet Blaster III coaster. “But someone has to do it.” The crew closes the hatch and you’re off down the totally frictionless track. Halfway down the 400-meter drop, however, the speedometer breaks. How can you record your top speed when you get to the bottom?

No problem; all you need is the principle of conservation of mechanical energy, which says that if the net work done by nonconservative forces is zero, the total mechanical energy of an object is conserved. You know that

You can make this equation a little easier. Your initial velocity is 0 and your final height is 0, so two of the terms will drop out when you plug in the numbers. You can then divide both sides by m, so you get

Much nicer. Solve for v2 by rearranging the terms and taking the square root of both sides:

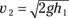
Then plugging in the numbers gives you the speed:

The coaster travels at 89 meters/second, or about 198 miles/hour, at the bottom of the track — should be fast enough for most kids.

Determining final height with mechanical energy

Besides determining variables such as final speed with the principle of conservation of mechanical energy, you can determine final height. At this very moment, for example, suppose Tarzan is swinging on a vine over a crocodile-infested river at a speed of 13.0 meters/second. He needs to reach the opposite river bank 9.0 meters above his present position in order to be safe. Can he swing it? The principle of conservation of mechanical energy gives you the answer:

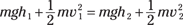
At Tarzan’s maximum height at the end of the swing, his speed, v2, will be 0 meters/second, and assuming h1 = 0 meters, you can relate h2 to v1 like this:

Solving for h2, this means that

Tarzan will come up 0.4 meters short of the 9.0 meters he needs to be safe, so he needs some help.

Powering Up: The Rate of Doing Work

Sometimes, it isn’t just the amount of work you do but the rate at which you do work that’s important. The concept of power gives you an idea of how much work you can expect in a certain amount of time.

Power in physics is the amount of work done divided by the time it takes, or the rate of work. Here’s what that looks like in equation form:

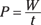
Assume you have two speedboats of equal mass, and you want to know which one will get you up to a speed of 120 miles per hour faster. Ignoring silly details like friction, you’ll need the same amount of work to get up to that speed, but how long it will take? If one boat takes three weeks to get you up to 120 miles per hour, that may not be the one you take to the races. In other words, the amount of work you do in a certain amount of time can make a big difference.

If the work done at any one instant varies, you may want to work out the average work done over the time t. An average quantity in physics is often written with a bar over it, as in the following equation for average power:

This section covers what units you’re dealing with and the various ways to find power.

Using common units of power

Power is work or energy divided by time, so power has the units of joules/second, which is called the watt — a familiar term for just about anybody who uses anything electrical. You abbreviate a watt as simply W, so a 100-watt light bulb converts 100 joules of electrical energy into light and heat every second.

You occasionally run across symbol conflicts in physics, such as the W for watts and the W for work. This conflict isn’t serious, however, because one symbol is for units (watts) and one is for a concept (work). Capitalization is standard, so be sure to pay attention to units versus concepts.

Note that because work and time are scalar quantities (they have no direction), power is a scalar as well.

Other units of power include foot-pounds per second (ft·lbs/s) and horsepower (hp). One hp = 550 ft·lbs/s = 745.7 W.

Say, for example, that you’re in a horse-drawn sleigh on the way to your grandmother’s house. At one point, the horse accelerates the sleigh with you on it, with a combined mass of 500 kilograms, from 1.0 meter/second to 2.0 meters/second in 2.0 seconds. How much power does the move take? Assuming no friction on the snow, the total work done on the sleigh, from the work-energy theorem, is

Plugging in the numbers gives you

Because the horse does this work in 2.0 seconds, the power needed is

One horsepower is 745.7 watts, so the horse is giving you about one-half horsepower — not too bad for a one-horse open sleigh.

Doing alternate calculations of power

Because work equals force times distance, you can write the equation for power the following way, assuming that the force acts along the direction of travel:

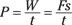
where s is the distance traveled. However, the object’s speed, v, is just s divided by t, so the equation breaks down to

That’s an interesting result — power equals force times speed? Yep, that’s what it says. However, because you often have to account for acceleration when you apply a force, you usually write the equation in terms of average power and average speed:

Here’s an example. Suppose your brother got himself a snappy new car. You think it’s kind of small, but he claims it has over 100 horsepower. “Okay,” you say, getting out your clipboard. “Let’s put it to the test.”

Your brother’s car has a mass of 1.10 × 103 kilograms. On the big Physics Test Track on the edge of town, you measure its acceleration as 4.60 meters/second2 over 5.00 seconds when the car started from rest. How much horsepower is that?

You know that , so all you need to calculate is the average speed and the net applied force. Take the net force first. You know that F = ma, so you can plug in the values to get

F = (1.10 × 103 kg)(4.60 m/s2) = 5,060 N

Okay, so the force applied to accelerate the car steadily is 5,060 newtons. Now all you need is the average speed. Say the starting speed was vi and the ending speed vf . You know that vi = 0 m/s, so what is vf? Well, you also know that because the acceleration was constant, the following equation is true:

vf = vi + at

As it happens, you know that acceleration and the time the car was accelerated over:

vf = 0 m/s + (4.60 m/s2)(5.00 s) = 23.0 m/s

Because the acceleration was constant, the average speed is

Because vi = 0 m/s, this breaks down to

Plugging in the numbers gives you the average velocity:

Great — now you know the force applied and the average speed. You can use the equation to find the average power. In particular

You still need to convert to horsepower. One horsepower = 745.7 watts, so

Therefore, the car developed an average of 78.0 horsepower, not 100 horsepower. “Rats,” says your brother. “I demand a recount.”

Okay, so you agree to calculate power another way. You know you can also calculate average power as work divided by time:

And the work done by the car is the difference in the beginning and ending kinetic energies:

W = KEf – KEi

The car started at rest, so KEi = 0 J. That leaves only the final kinetic energy to calculate:

Plugging in the numbers gives you:

So because and the work done was 2.91 × 105 joules in 5.00 seconds, you get the following:

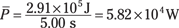
And, as before

“Double rats,” your brother says.