Chapter 10

Putting Objects in Motion: Momentum and Impulse

In This Chapter

Checking your impulse

Gaining knowledge about momentum

Intertwining impulse and momentum

Utilizing the conservation of momentum

Examining different types of collisions

Both momentum and impulse are very important to kinematics, or the study of objects in motion. After you have these topics under your belt, you can start talking about what happens when objects collide (hopefully not your car or bike). Sometimes they bounce off each other (like when you hit a tennis ball with a racket), and sometimes they stick together (like when a dart hits a dart board). With the knowledge of impulse and momentum you pick up in this chapter, you can handle either case.

Looking at the Impact of Impulse

In physics terms, impulse tells you how much the momentum of an object will change when a force is applied for a certain amount of time. Say, for example, that you’re shooting pool. Instinctively, you know how hard to tap each ball to get the results you want. The nine ball in the corner pocket? No problem — tap it and there it goes. The three ball bouncing off the side cushion into the other corner pocket? Another tap, this time a little stronger.

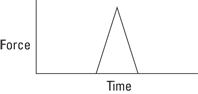
The taps you apply are called impulses. Take a look at what happens on a microscopic scale, millisecond by millisecond, as you tap a pool ball. The force you apply with your cue appears in Figure 10-1. The tip of each cue has a cushion, so the impact of the cue is spread out over a few milliseconds as the cushion squashes slightly. The impact lasts from the time when the cue touches the ball, ti, to the time when the ball loses contact with the cue, tf. As you can see from Figure 10-1, the force exerted on the ball changes during that time; in fact, it changes drastically, and figuring out what the force was doing at any 1 millisecond would be hard without some fancy equipment.

Figure 10-1: Examining force versus time gives you the impulse you apply on objects.

Because the pool ball doesn’t come with any fancy equipment, you have to do what physicists normally do, which is to talk in terms of the average force over time. You can see what that average force looks like in Figure 10-2. Speaking as a physicist, you say that the impulse — or the tap — that the pool cue provides is the average force multiplied by the time that you apply the force.

Here’s the equation for impulse:

Figure 10-2: The average force over a time interval depends on the values the force has over that time.

Note that this equation is a vector equation, meaning it deals with both direction and magnitude (see Chapter 4). Impulse, J, is a vector, and it’s in the same direction as the average force (which itself may be a net vector sum of other forces).

You get impulse by multiplying a quantity with units of newtons by a quantity with units of seconds, so the units of impulse are newton-seconds in the MKS system and pound-seconds in the FPS system. (See Chapter 2 for details on systems of measurement.)

Gathering Momentum

In physics terms, momentum is proportional to both mass and velocity, and to make your job easy, physics defines momentum as the product of mass times velocity. Momentum is a big concept both in introductory physics and in some advanced topics such as high-energy particle physics, where the components of atoms zoom around at high speeds. When the particles collide, you can often predict what will happen based on your knowledge of momentum.

Even if you’re unfamiliar with the physics of momentum, you’re already familiar with the general idea. Catching a runaway car going down a steep hill is a problem because of its momentum. If a car without any brakes is speeding toward you at 40 miles per hour, trying to stop it by standing in its way may not be a great idea. The car has a lot of momentum, and bringing it to a stop requires plenty of effort. Now think of an oil tanker. Its engines aren’t strong enough to make it turn or stop on a dime. Therefore, an oil tanker can take 20 miles or more to come to a stop, all because of the ship’s momentum.

The more mass that’s moving, the more momentum the mass has. The greater the magnitude of its velocity (think of an even faster oil tanker), the more momentum it has. The symbol for momentum is p, so you can say that

p = mv

Momentum is a vector quantity, meaning that it has a magnitude and a direction (see Chapter 4). The magnitude is in the same direction as the velocity — all you have to do to get the momentum of an object is to multiply its mass by its velocity. Because you multiply mass by velocity, the units for momentum are kilogram-meters per second (kg·m/s) in the MKS system.

The Impulse-Momentum Theorem: Relating Impulse and Momentum

You can connect the impulse you give to an object — like striking a pool ball with a cue — with the object’s change in momentum; all you need is a little algebra and the process you explore in this section, called the impulse-momentum theorem. What makes the connection easy is that you can play with the equations for impulse and momentum to simplify them so you can relate the two topics. What equations does physics have in its arsenal to connect these two? Relating force and velocity is a start. For example, force equals mass times acceleration (see Chapter 5), and the definition of average acceleration is

where v stands for velocity and t stands for time. Now you may realize that if you multiply that equation by the mass, you get force, which brings you closer to working with impulse:

Now you have force in the equation. To get impulse, multiply the force equation by Δt, the time over which you apply the force:

Take a look at the final expression, mΔv. Because momentum equals mv (see the section “Gathering Momentum” earlier in this chapter), this is just the difference in the object’s initial and final momentum: pf – pi = Δp. Therefore, you can add that to the equation:

FΔt = Δp

Now take a look at the term on the left, FΔt. That’s the impulse, J (see the section “Looking at the Impact of Impulse” earlier in this chapter), or the force applied to the object multiplied by the time that force was applied. Therefore, you can write this equation as

J = FΔt = Δp

Getting rid of everything in the middle finally gives you the impulse-momentum theorem, which says that impulse equals change in momentum:

J = Δp

The rest of this section provides some examples so you can practice this equation. But before you set off, think about what the formula means for the relation among impulse, force, and momentum. The impulse-momentum theorem defines a very simple relation between the impulse and momentum, namely that impulse is equal to the change in momentum. You can also see how a constant force applied over a time is equal to an impulse that is given by the force multiplied by the time:

J = FΔt

Last, you can tie the force and momentum together through the impulse, which gives you

FΔt = Δp

The meaning of this relation may become clearer if you divide both side by Δt:

So you see that the force is given by the rate of change of momentum. This is a whole new way of thinking about force! Wherever you see momentum changing with time, you know a force is acting, and if calculating the momentum is easier, it can lead to an easier way of calculating the force. Check out the following examples.

Shooting pool: Finding force from impulse and momentum

With the equation J = Δp, you can relate the impulse with which you hit an object to its consequent change in momentum. How about using the equation the next time you hit a pool ball? You line up the shot that the game depends on. You figure that the end of your cue will be in contact with the ball for 5 milliseconds (a millisecond is a thousandth of a second).

You measure the ball at 200 grams (or 0.200 kilograms). After testing the side cushion with calipers, spectroscope, and tweezers, you figure that you need to give the ball a speed of 2.0 meters per second. What average force do you have to apply? To find the average force, first find the impulse you have to supply. You can relate that impulse to the change in the ball’s momentum this way:

J = Δp = pf – pi

Because the pool ball doesn’t change direction, you can use this equation for the component of the pool ball’s momentum in the direction in which you strike it. Because you’re using a component of the vector, you remove the bold from p.

So what’s the change in the ball’s momentum? The speed you need, 2.0 meters per second, is the magnitude of the pool ball’s final velocity. Assuming the pool ball starts at rest, the change in the ball’s momentum will be the following:

Δp = pf – pi = m(vf – vi)

Where v is the component of the ball’s velocity in the direction in which you strike it. Plugging in the numbers gives you the change in momentum:

Δp = m(vf – vi) = (0.200 kg)(2.0 m/s – 0.0 m/s) = 0.40 kg·m/s

You need a change in momentum of 0.40 kilogram-meters per second, which is also the impulse you need. Because J = FΔt, this equation becomes the following for the component of the force in the direction of motion:

FΔt = 0.40 kg·m/s

Therefore, the force you need to apply works out to be

In this equation, the time your cue ball is in contact with the ball is 5 milliseconds, or 5.0 × 10–3 seconds. Plug in the time to find the force:

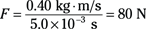
You have to apply about 80 newtons (or about 18 pounds) of force, which sounds like a huge amount. However, you apply it over such a short time, 5.0 × 10–3 seconds, that it seems like much less.

Singing in the rain: An impulsive activity

After a triumphant evening at the pool hall, you decide to leave and discover that it’s raining. You grab your umbrella from your car, and the handy rain gauge on the umbrella’s top tells you that 100 grams of water are hitting the umbrella each second at an average speed of 10 meters per second. If the umbrella has a total mass of 1.0 kilograms, what force do you need to hold it upright in the rain?

Figuring the force you usually need to hold the weight of the umbrella is no problem — you just figure mass times the acceleration due to gravity (F = ma), or (1.0 kg)(9.8 m/s2) = 9.8 N.

But what about the rain falling on your umbrella? Even if you assume that the water falls off the umbrella immediately, you can’t just add the weight of the water, because the rain is falling with a speed of 10 meters per second; in other words, the rain has momentum. What can you do? You know that you’re facing 100 grams (0.10 kilograms) of water falling onto the umbrella each second at a velocity of 10 meters per second downward. When that rain hits your umbrella, the water comes to rest, so the change in momentum of rain every second is

Δp = mΔv

You’re considering only the vertical components of the vectors, so the variables aren’t in bold. Plugging in numbers gives you the change in momentum:

Δp = mΔv = (0.10 kg)(10 m/s) = 1.0 kg·m/s

The rain’s change in momentum, every second, as it hits your umbrella is 1.0 kilogram-meter per second. You can relate that change to force with the impulse-momentum theorem, which tells you that

FΔt = Δp

Dividing both sides by Δt allows you to solve for the force, F:

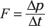
You know that Δp = 1.0 kg·m/s in 1.0 second, so plugging in Δp and setting Δt to 1.0 second gives you the force of the rain:

In addition to the 9.8 newtons of the umbrella’s weight, you need 1.0 newton to stand up to the falling rain as it drums on the umbrella, for a total of 10.8 newtons, or about 2.4 pounds of force.

When Objects Go Bonk: Conserving Momentum

The principle of conservation of momentum states that when you have an isolated system with no external forces, the initial total momentum of objects before a collision equals the final total momentum of the objects after the collision. In other words, Σpi = Σpf.

You may have a hard time dealing with the physics of impulses because of the short times and the irregular forces. But with the principle of conservation, items that are hard to measure — for example, the force and time involved in an impulse — are out of the equation altogether. Thus, this simple principle may be the most useful idea I provide in this chapter.

Deriving the conservation formula

You can derive the principle of conservation of momentum from Newton’s laws, what you know about impulse, and a little algebra.

Say that two careless space pilots are zooming toward the scene of an interplanetary crime. In their eagerness to get to the scene first, they collide. During the collision, the average force the second ship exerts on the first ship is F12. By the impulse-momentum theorem (see the section “The Impulse-Momentum Theorem: Relating Impulse and Momentum”), you know the following for the first ship:

F12Δt = Δp1 = m1Δv1 = m1(vf1 – vi1)

And if the average force exerted on the second ship by the first ship is F21, you also know that

F21Δt = Δp2 = m2Δv2 = m2(vf2 – vi2)

Now you add these two equations together, which gives you the resulting equation:

F12Δt + F21Δt = m1(vf1 – vi1) + m2(vf2 – vi2)

Distribute the mass terms and rearrange the terms on the right until you get the following:

F12Δt + F21Δt = m1vf1 – m1vi1 + m2vf2 – m2vi2

F12Δt + F21Δt = (m1vf1 + m2vf2) – (m1vi1 + m2vi2)

This is an interesting result, because m1vi1 + m2vi2 is the initial total momentum of the two rocket ships (p1i + pi2) and m1vf1 + m2vf2 is the final total momentum (p1f + p2f) of the two rocket ships. Therefore, you can write this equation as follows:

F12Δt + F21Δt = (p1f + p2f) – (p1i + pi2)

If you write the initial total momentum as pf and the final total momentum as pi, the equation becomes

F12Δt + F21Δt = pf – pi

Where do you go from here? Both terms on the left include Δt, so you can rewrite F12Δt + F21Δt as the sum of the forces involved, ΣF, multiplied by the change in time:

ΣFΔt = pf – pi

If you’re working with what’s called an isolated or closed system, you have no external forces to deal with. Such is the case in space. If two rocket ships collide in space, there are no external forces that matter, so by Newton’s third law (see Chapter 5), F12Δt = –F21Δt. In other words, when you have a closed system, you get the following:

ΣFΔt = pf – pi

0 = pf – pi

This converts to

pf = pi

The equation pf = pi says that when you have an isolated system with no external forces, the initial total momentum before a collision equals the final total momentum after a collision, giving you the principle of conservation of momentum.

Finding velocity with the conservation of momentum

You can use the principle of conservation of momentum to measure other characteristics of motion, such as velocity. Say, for example, that you’re out on a physics expedition and you happen to pass by a frozen lake where a hockey game is taking place. You measure the speed of one player as 11.0 meters per second just as he collides, rather brutally for a pick-up game, with another player initially at rest. You watch with interest, wondering how fast the resulting mass of hockey players will slide across the ice. After asking a few friends in attendance, you find out that the first player has a mass of 100 kilograms and the bulldozed player (who turns out to be his twin) also has a mass of 100 kilograms. So what’s the final speed of the player tangle?

You’re dealing with a closed system, because you neglect the force of friction here, and although the players are exerting a force downward on the ice, the normal force (see Chapter 5) is exerting an equal and opposite force on them; therefore, the vertical force sums to zero.

But what about the resulting horizontal speed along the ice? Due to the principle of conservation of momentum, you know that

pf = pi

Imagine that the collision is head on, so all the motion occurs in one dimension — along a line. So you only need to examine the components of the vector quantities in this single dimension. The component of a vector in one dimension is just a number, so I don’t write them in bold.

The victim isn’t moving before the hit, so he starts without any momentum. Therefore, the initial momentum, pi, is simply the initial momentum of the enforcer, Player 1. To put this equation into more helpful terms, substitute Player 1’s mass and initial velocity (m1vi1) for the initial momentum (pi):

pi = m1vi1

After the hit, the players tangle up and move with the same final velocity. Therefore, the final momentum, pf, must equal the combined mass of the two players multiplied by their final velocity, (m1 + m2)vf, which gives you the following equation:

(m1 + m2)vf = m1vi1

Solving for vf gives you the equation for their final velocity:

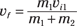
Plugging in the numbers gives you the answer:

The speed of the two players together will be half the speed of the original player. That may be what you expected, because you end up with twice the moving mass as before; because momentum is conserved, you end up with half the speed. Beautiful. You note the results down on your clipboard.

Finding firing velocity with the conservation of momentum

The principle of conservation of momentum comes in handy when you can’t measure velocity with a simple stopwatch. Say, for example, that you accept a consulting job from an ammunition manufacturer that wants to measure the muzzle velocity of its new bullets. No employee has been able to measure the velocity yet, because no stopwatch is fast enough. What do you do? You decide to arrange the setup shown in Figure 10-3, where you fire a bullet of mass m1 into a hanging wooden block of mass m2.

The directors of the ammunition company are perplexed — how can your setup help? Each time you fire a bullet into a hanging wooden block, the bullet kicks the block into the air. So what? You decide they need a lesson on the principle of conservation of momentum. The original momentum, you explain, is the momentum of the bullet:

pi = mvi

Because the bullet sticks in the wooden block, the final momentum is the product of the total mass, m1 + m2, and the final velocity of the bullet/wooden block combination:

pf = (m1 + m2)vf

Figure 10-3: Shooting a wooden block on a string allows you to experiment with velocity, but don’t try this at home!

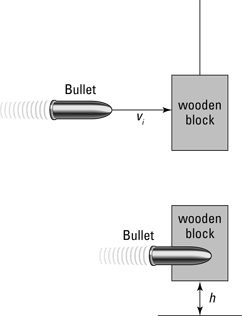
Because of the principle of conservation of momentum, you can say that

pf = pi

Therefore, you can plug in the earlier expressions for final and initial momentum:

The directors start to get dizzy, so you explain how the kinetic energy of the block when it’s struck goes into its final potential energy when it rises to height h (see Chapter 9). Here’s how you can represent the bullet’s kinetic energy and the bullet-and-block’s change in potential energy:

You can plug in the value of vf, which gives you

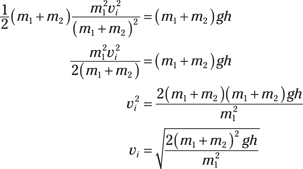
With a flourish, you explain that solving for vi gives you the bullet’s initial velocity:

You measure that the bullet has a mass of 50 grams, that the wooden block has a mass of 10.0 kilograms, and that upon impact, the block rises 50.0 centimeters into the air. Plugging in those values gives you your result:

The initial velocity is 630 meters per second, which converts to about 2,070 feet per second. “Brilliant!” the directors cry as they hand you a big check.

When Worlds (Or Cars) Collide: Elastic and Inelastic Collisions

Examining collisions in physics can be pretty entertaining, especially because the principle of conservation of momentum makes your job so easy (see the earlier section “When Objects Go Bonk: Conserving Momentum”). But when you’re dealing with collisions, there’s often more to the story than impulse and momentum. Sometimes, kinetic energy is also conserved, which gives you the extra edge you need to figure out what happens in all kinds of collisions, even across two dimensions.

Collisions are important in many physics problems. Two cars collide, for example, and you need to find the final velocity of the two when they stick together. You may even run into a case where two railway cars going at different velocities collide and couple together, and you need to determine the final velocity of the two cars.

But what if you have a more general case where the two objects don’t stick together? Say, for example, you have two pool balls that hit each other at different speeds and at different angles and bounce off with different speeds and different angles. How the heck do you handle that situation? You have a way to handle these collisions, but you need more than just the principle of conservation of momentum gives you. In this section, I explain the difference between elastic and inelastic collisions and then do a few elastic-collision problems.

Determining whether a collision is elastic

When bodies collide in the real world, they sometimes squash and deform to some degree. The energy to perform the deformation comes from the objects’ original kinetic energy. In other cases, friction turns some of the kinetic energy into heat. Physicists classify collisions in closed systems (where the net forces add up to zero) based on whether colliding objects lose kinetic energy to some other form of energy:

Elastic collision: In an elastic collision, the total kinetic energy in the system is the same before and after the collision. If losses to heat and deformation are much smaller than the other energies involved, such as when two pool balls collide and go their separate ways, you can generally ignore the losses and say that kinetic energy was conserved.

Inelastic collision: In an inelastic collision, the collision changes the total kinetic energy in a closed system. In this case, friction, deformation, or some other process transforms the kinetic energy. If you can observe appreciable energy losses due to nonconservative forces (such as friction), kinetic energy isn’t conserved.

You see inelastic collisions when objects stick together after colliding, such as when two cars crash and weld themselves into one. However, objects don’t need to stick together in an inelastic collision; all that has to happen is the loss of some kinetic energy. For example, if you smash your car into a car and deform it, the collision is inelastic, even if you can drive away after the accident.

Regardless of whether a collision is elastic or inelastic, momentum is always the same before and after the collision, as long as you have a closed system.

Colliding elastically along a line

When a collision is elastic, kinetic energy is conserved. The most basic way to look at elastic collisions is to examine how the collisions work along a straight line. If you run your bumper car into a friend’s bumper car along a straight line, you bounce off and kinetic energy is conserved along the line. But the behavior of the cars depends on the mass of the objects involved in the elastic collision.

Bumping into a heavier mass

You take your family to the Physics Amusement Park for a day of fun and calculation, and you decide to ride the bumper cars. You wave to your family as you speed your 300-kilogram car-and-driver up to 10.0 meters per second. Suddenly, Bonk! What happened? The 400-kilogram car-and-driver in front of you had come to a complete stop, and you rear-ended the car elastically; now you’re traveling backward and the other car is traveling forward. “Interesting,” you think. “I wonder if I can solve for the final velocities of both bumper cars.”

You know that the momentum was conserved, and you know that the car in front of you was stopped when you hit it, so if your car is Car 1 and the other is Car 2, you get the following:

m1vf1 + m2vf2 = m1vi1

However, this doesn’t tell you what vf1 and vf2 are, because you have two unknowns and only one equation here. You can’t solve for vf1 or vf2 exactly in this case, even if you know the masses and vi1. You need some other equations relating these quantities. How about using the conservation of kinetic energy? The collision was elastic, so kinetic energy was conserved. KE = (1/2)mv2, so here’s your equation for the two cars’ final and initial kinetic energies:

Now you have two equations and two unknowns, vf1 and vf2, which means you can solve for the unknowns in terms of the masses and vi1. You have to dig through a lot of algebra here because the second equation has many squared velocities, but when the dust settles, you get the following two equations:

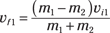
Now you have vf1 and vf2 in terms of the masses and vi1. Plugging in the numbers gives you the two bumper cars’ final velocities. Here’s the velocity of your car:

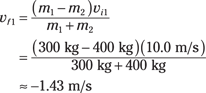
And here’s the final velocity of the other guy:

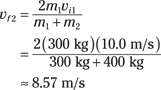
The two speeds tell the whole story. You started off at 10.0 meters per second in a bumper car of 300 kilograms, and you hit a stationary bumper car of 400 kilograms in front of you. Assuming the collision took place directly and the second bumper car took off in the same direction you were going before the collision, you rebounded at –1.43 meters per second — backward, because this quantity is negative and the bumper car in front of you had more mass — and the bumper car in front of you took off at a speed of 8.57 meters per second.

Bumping into a lighter mass

After having a bad experience in a previous trip to the bumper car pit — where your light bumper car rear-ended a heavy bumper car (see the preceding section for the calculation) — you decide to go back and pick on some poor light cars in a monster bumper car. What happens if your bumper car (plus driver) has a mass of 400 kilograms and you rear-end a stationary 300-kilogram car? In this case, you use the equation for conservation of kinetic energy, the same formula you use in the preceding section. Here’s what your final velocity comes out to:

The little car’s final velocity comes out to

In this case, you don’t bounce backward. The lighter, stationary car takes off after you hit it, but not all your forward momentum is transferred to the other car. Is momentum still conserved? Here are your formulas for the initial and final momentums:

pi = m1vi1

pf = m1vf1 + m2vf2

Putting in the numbers, here’s the initial momentum:

pi = m1vi1 = (400 kg)(10.0 m/s) = 4,000 kg·m/s

And here’s the final momentum:

pf = m1vf1 + m2vf2

= (400 kg)(1.43 m/s) + (300 kg)(11.4 m/s)

≈ 4,000 kg∙m/s

The numbers match, so momentum is conserved in this collision, just as it is for your collision with a heavier car.

Colliding elastically in two dimensions

Collisions don’t always occur along a straight line. For example, balls on a pool table can travel in two dimensions, both x and y, as they roll around. Collisions along two dimensions introduce variables such as angle and direction.

Say, for example, that your physics travels take you to the golf course, where two players are lining up for their final putts of the day. The players are tied, so these putts are the deciding shots. Unfortunately, the player closer to the hole breaks etiquette, and both golfers putt at the same time. Their 45-gram golf balls collide! You can see what happens in Figure 10-4.

Figure 10-4: Before, during, and after a collision between two balls moving in two dimensions.

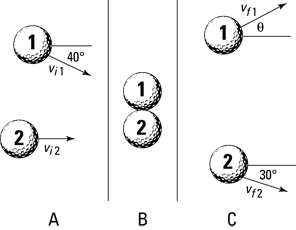
You quickly stoop down to measure all the angles and velocities involved in the collision. You measure the speeds: vi1 = 1.0 meter per second, vi2 = 2.0 meters per second, and vf2 = 1.2 meters per second. You also measure most of the angles, as Figure 10-4 shows. However, you can’t get the final angle and speed of Ball 1.

Because the golf balls collide elastically, both momentum and kinetic energy are conserved. In particular, momentum is conserved in both the x and y directions, and total kinetic energy is conserved as well. You need both of these conservations to find the final speed and direction of Ball 1.

First work out the final speed of Ball 1. Because the masses of the balls are equal, you can call each mass m. The initial total kinetic energy (for both balls) is

Then the final kinetic energy is given by

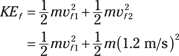
Then because kinetic energy is conserved, the final kinetic energy must be equal to the initial kinetic energy, and so you can write

Then you can rearrange the equation to isolate the term with the final velocity of Ball 1, vf1:

Then if you solve for vf1 (divide both sides by m, multiply both sides by 2, and take the square root), you get

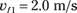
So there you have it: The final speed of Ball 1 is 2.0 meters per second.

To work out the angle of Ball 1’s velocity, you use the conservation of momentum. Momentum is conserved in both the x and y directions, so the following equations are true:

pfx = pix

pfy = piy

In other words, the final momentum in the x direction is the same as the initial momentum in the x direction, and the final momentum in the y direction is the same as the initial momentum in the y direction. Here’s what the initial momentum in the x direction looks like:

pix = mvi1 cos 40° + mvi2

You can see that this is the sum of the x momenta of both balls.

The final momentum in the x direction is given by

pfx = mvf1 cos θ + mvf2 cos 30°

The x component of momentum is conserved, so you can equate the initial and final momenta in the x direction:

mvi1 cos 40° + mvi2 = mvf1 cos θ + mvf2 cos 30°

Divide both sides by m to get

vi1 cos 40° + vi2 = vf1 cos θ + vf2 cos 30°

If you rearrange this equation to put the term with the unknown angle, θ, on one side, you get

vf1 cos θ = vi1 cos 40° + vi2 – vf2 cos 30°

Dividing by vf1 gives you

Plug in the measured values and the final speed of Ball 1 you calculated previously to get

Finally, you can take the inverse cosine of each side to find the angle:

θ ≈ 30°

So there you have it: After the collision, Ball 1 moves with a velocity of 2.0 m/s at an angle of 30° from horizontal. You have combined the use of conservation of kinetic energy (in an elastic collision) and conservation of momentum (as in all collisions) to work out the final velocity of Ball 1.