Chapter 14
Turning Up the Heat with Thermodynamics
In This Chapter
 Taking temperature in Fahrenheit, Celsius, and Kelvin
Taking temperature in Fahrenheit, Celsius, and Kelvin
 Examining temperature change with thermal expansion
Examining temperature change with thermal expansion
 Following along with heat flow
Following along with heat flow
 Accounting for specific heat capacity
Accounting for specific heat capacity
 Meeting the requirements for phase change
Meeting the requirements for phase change
The concepts of heat and temperature are part of your daily life. Under-standing the laws that govern the temperatures of things, how heat flows between them, and how the material and thermal properties depend on each other hasn’t only furthered physicists’ appreciation of the world and its workings; it has also led to technological and engineering advances. A structurally sound bridge, for example, depends on understanding the thermal expansion of any of the bridge’s metal elements. The motor car works because of the thermal energy released from the combustion of gasoline and air. These, and more, are possible only with an understanding of the relationship between materials and their thermal properties.
This chapter explores heat and temperature. Physics gives you plenty of power to predict what goes on when things heat up or cool down. I discuss temperature scales, linear expansion, volume expansion, and how much of liquid at one temperature will change the temperature of another when they’re put together.
Measuring Temperature
Temperature is a measure of molecular movement — how fast and how much the molecules of whatever substance you’re measuring are moving. You always start a calculation or observation in physics by making measurements, and when you’re discussing temperature, you have several scales at your disposal: most notably, Fahrenheit, Celsius, and Kelvin.
Fahrenheit and Celsius: Working in degrees
In the United States, the most common temperature scale is the Fahrenheit scale, which measures temperature in degrees. For example, the blood temperature of a healthy human being is 98.6°F — the F means you’re using the Fahrenheit scale. In Fahrenheit’s system, pure water freezes at 32°F and boils at 212°F.
However, the Fahrenheit system wasn’t very reproducible in its early days, so scientists developed another system — the Celsius scale (formerly called the centigrade system). Using this system, pure water freezes at 0°C and boils at 100°C. Here’s how you tie the two systems of temperature measurement together (these measurements are at sea level; they change as you go up in altitude):
 Freezing water: 32°F = 0°C
Freezing water: 32°F = 0°C
 Boiling water: 212°F = 100°C
Boiling water: 212°F = 100°C
If you do the math, you find 180°F between the points of freezing and boiling in the Fahrenheit system and 100°C in the Celsius system, so the conversion ratio is 180/100 = 18/10 = 9/5. And don’t forget that the measurements are also offset by 32 degrees (the 0-degrees point of the Celsius scale corresponds to the 32-degrees point of the Fahrenheit scale). Putting these ideas together lets you convert from Celsius to Fahrenheit or from Fahrenheit to Celsius pretty easily; just remember these equations:




For example, the blood temperature of a healthy human being is 98.6°F. What does this equal in Celsius? Just plug in the numbers:
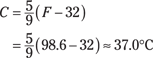
Zeroing in on the Kelvin scale
In the 19th century, William Thompson created a third temperature system, one now in common use in physics — the Kelvin system (Thompson later became Lord Kelvin). The Kelvin system has become so central to physics that the Fahrenheit and Celsius systems are defined in terms of the Kelvin system — a system based on the concept of absolute zero.
Analyzing absolute zero
Molecules move more and more slowly as the temperature lowers. At absolute zero, the molecules almost stop, which means you can’t cool them anymore. (The molecules only “almost” stop because when you get down to the scale of molecules, you’re in the realm of quantum mechanics. When the molecules have as little energy as possible, they still have zero-point energy.) No refrigeration system in the world — or in the universe — can go any lower than absolute zero.
The Kelvin system uses absolute zero as its zero point, which makes sense. What’s a little odd is that you don’t measure temperature in this scale in degrees; you measure it in kelvins. A temperature of 100 is 100 kelvins (not 100 degrees Kelvin) in the Kelvin scale. This system has become so widely adopted that the official MKS unit of temperature is the kelvin (in practice, however, you see °C used more often in introductory physics).
Making kelvin conversions
 Celsius to Kelvin: K = C + 273.15
Celsius to Kelvin: K = C + 273.15
 Kelvin to Celsius: C = K – 273.15
Kelvin to Celsius: C = K – 273.15
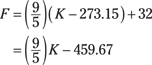
(Or you can convert kelvins to degrees Celsius and then use the conversion formulas in the earlier section “Fahrenheit and Celsius: Working in degrees.”)
At what temperature does water boil in kelvins? Well, pure water boils at 100°C at sea level, so plug your numbers into the formula:
K = C + 273.15
= 100 + 273.15 = 373.15 K
Water boils at 373.15 kelvins. Helium turns to liquid at 4.2 kelvins; what’s that in degrees Celsius? Use the formula:
C = K – 273.15
= 4.2 – 273.15 = –268.95°C
Helium liquefies at –268.95°C. Pretty chilly.
The Heat Is On: Thermal Expansion
Some screw-top jars can be tough to open, which is maddening when you really want some pickles. Maybe you remember seeing your mom run stubborn jar lids under hot water when you were a kid. She did this because heat makes the lid expand, which usually makes the job of turning it much easier.
On a molecular level, thermal expansion happens because when you heat objects, the molecules bounce around faster, which leads to a physical expansion. (Note that this relationship between heating and expanding isn’t true for all materials, however. For example, water becomes denser as you raise its temperature from 0°C to 4°C.)
In this section, I first cover the linear expansion of solids — how solid objects lengthen when temperature rises. I then discuss thermal expansion in 3-D so you can observe volume changes in both solids and liquids. (For info on thermal expansion in gases, flip to Chapter 16.)
Linear expansion: Getting longer
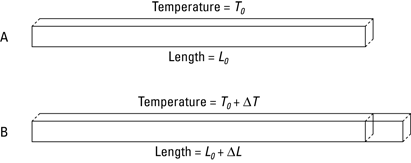
When you talk about the expansion of a solid in any one dimension under the influence of heat, you’re talking about linear expansion. Figure 14-1 shows an image of this phenomenon.
Figure 14-1: Linear expansion usually takes place when you apply heat to solids.
Relating temperature changes to changes in length
Under thermal expansion, a solid object’s change in length, ΔL, is proportional to the change in temperature, ΔT. You can show this relationship mathematically.
Note: Even though initial values are represented by a subscript i in other chapters (Li, for example), I use a subscript 0 (L0, for example), which is what you’re more likely to see in other texts for these kinds of equations.
First, suppose you raise the temperature of an object a small amount:
T = T0 + ΔT
where T represents the final temperature, T0 represents the original temperature, and ΔT represents the change in temperature. The change of temperature results in an expansion in any linear direction of
L = L0 + ΔL
where L represents the final length of the solid, L0 represents its original length, and ΔL represents the change in length.
When you heat a solid, the solid expands by a few percent, and that percentage is proportional to the change in temperature. In other words, ΔL/L0 (the fraction by which the solid expands) is proportional to ΔT (the change in temperature).
The constant of proportionality, which helps tell you exactly how much an object will expand, depends on which material you’re working with. The constant of proportionality is the coefficient of linear expansion, which you give the symbol α. You can write this relationship as an equation this way:
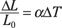
ΔL = αL0ΔT
Physics problems provide these coefficients when you need them to solve the problem. But just in case, here’s a useful website that lists many of the coefficients: www.engineeringtoolbox.com/linear-expansion-coefficients-d_95.html.
Workin’ on the railroad: A linear expansion example
Plenty of construction projects take linear expansion into account. You often see bridges with “expansion joints” connecting the bridge to the road surface. As temperatures rise, these joints allow the bridge materials to expand without buckling.
Here’s a construction-based example. Say that you’re called in to check out a new railroad. You look closely at the 10.0-meter-long rails, noticing that they’re only 1.0 millimeter apart at the ends. “How much hotter does it get around these parts during the summer?” you ask.
“Hotter?” the chief designer guffaws. “You afraid the rails will melt?”
Everyone snickers at your ignorance as you check your almanac, which tells you that you can expect the rails to get 50°C hotter during a normal summer. The coefficient of linear expansion for the steel that the rails are made from is approximately 1.2 × 10–5°C–1. So how much will the typical rail expand during the hot part of summer? You know that
ΔL = αL0ΔT
Plugging in the numbers gives you the expansion:
ΔL = αL0ΔT = (1.2 × 10–5°C–1)(10.0 m)(50°C–1 ) = 6.0 × 10–3 m
In other words, you can expect the rails to expand 6.0 × 10–3 meters, or 6.0 millimeters, in the summer. However, the rails are only 1.0 millimeter apart. The railroad company is in trouble.
You look at the chief designer and say, “You and I are about to have a nice, long talk about physics.”
Volume expansion: Taking up more space
Linear expansion, as the name indicates, takes place in one dimension, but the world comes with three dimensions. If an object undergoes a small temperature change of just a few degrees, you can say that the volume of the solid or liquid will change in a way proportionate to the temperature change. As long as the temperature differences involved are small, the fraction by which the solid expands, ΔV/V0, is proportional to the change in temperature, ΔT (where ΔV represents the change in volume and V0 represents the original volume).
With volume expansion, the constant involved is called the coefficient of volume expansion. This constant is given by the symbol β, and like α, it’s often measured in °C–1. Using β, here’s how you can express the equation for volume expansion:
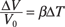
ΔV = βV0ΔT
You’ve created the analog (or equivalent) of the equation ΔL = αL0ΔT for linear expansion (see the earlier section “Linear expansion: Getting longer”).
Tanker trucks: Looking at expanding liquids
Say you’re at the gasoline refinery when you notice that workers are filling all the 5,000-gallon tanker trucks to the very brim before driving off on a hot summer day. “Uh oh,” you think as you get your calculator out. For gasoline, β = 9.5 × 10–4°C–1, and you figure that it’s 10.0°C warmer in the sunshine than in the building, so here’s how much the volume of gasoline will increase:
ΔV = βV0ΔT = (9.5 × 10–4°C–1)(5,000 gal)(10.0°C) = 47.5 gal
Not good news for the refinery — those 5,000-gallon tankers of gasoline that are filled to the brim have to carry 5,047.5 gallons of gasoline after they go out in the sunshine. The gas tanks may also expand, but the β of steel is much less than the β of gasoline. Should you tell the refinery workers? Or should you ask for a bigger fee first?
First you negotiate your whopper fee, and then you go explain the problem to the foreman. “Holy smokes!” he cries. “We’d have gasoline pouring out of the caps on the top of our trucks.” He stops the trucks and gets some gasoline taken out of each before they’re sent on their way.
Radiators: Seeing expanding liquids and containers
The foreman of a gasoline refinery notices that his workers are filling the radiators of the trucks full up to the brim. “Holy smokes!” he cries. “What about volume expansion? The coolant will be pouring out of those radiators when they get hot.” True, the coolant will expand. But doesn’t everyone fill radiators to the brim?
Most cars have a plastic overflow reservoir that catches the overflow as it happens. So are the gasoline company’s radiators safe? Each radiator holds 15 quarts of coolant, which is 1.4 × 10–2 cubic meters, and has a 1-quart coolant reservoir, which is 9.5 × 10–4 cubic meters. Will a radiator overflow more than the reservoir can handle?
You get out your clipboard. Okay, the radiator takes 15 quarts (1.4 × 10–2 m3) of coolant, and you happen to know that the β for the coolant is β = 4.1 × 10–4°C–1.You want to be precise this time and take into account the expansion of the radiator as well. The radiator is made of copper (with a thin outer layer of aluminum, which you can neglect in this example), so β = 5.1 × 10–5°C–1. If the radiator starts at 20°C and heats up to its working temperature of 92°C, will a 1-quart (9.5 × 10–4 m3) coolant reservoir be enough to catch the overflow?
The foreman watches tensely as you begin your calculations. Here’s the formula for the expansion of the coolant:
ΔVc = βcV0cΔT
You know that βc = 4.1 × 10–4°C–1, V0c = 1.4 × 10–2 m3, and ΔT = 92°C – 20°C = 72°C in this example. Plug in these numbers and solve:
ΔVc = βcV0cΔT = 4.2 × 10–4 m3
Okay, so the coolant will expand by 4.2 × 10–4 m3, which is equal to 0.44 quarts. But the radiator will also expand, meaning it can hold more coolant. This time, you take that expansion into account to get a more accurate answer.
Because the radiator is made of copper, it’ll expand as though it were made of solid copper, which makes the math easier. Here’s the change in volume for the radiator:
ΔVr = βrV0rΔT
Here, βr = 5.1 × 10–5°C–1, ΔV0r = 1.4 × 10–2 m3, and ΔT = 92°C – 20°C = 72°C. Plug in your numbers and solve:
ΔVr = βrV0rΔT
= (5.1 × 10–5°C–1)(1.4 × 10–2 m3)(72°C)
≈ 5.2 × 10–5 m3
The total overflow is equal to the coolant expansion minus the amount the radiator expands, so plug in your numbers:
ΔV = ΔVc – ΔVr
= 4.2 × 10–4 m3 – 5.2 × 10–5 m
≈ 3.7 × 10–4 m3
So each radiator will overflow a little more than a third of a quart, and the overflow reservoir is 1 quart in volume. You turn to the foreman and say, “The radiators are fine, with a good safety margin.”
“Whew,” says the foreman.
Heat: Going with the Flow (Of Thermal Energy)
What, really, is heat? When you touch a hot object, heat flows from the object to you, and your nerves record that fact. When you touch a cold object, heat flows from you to that object, and again, your nerves keep track of what’s happening. Your nerves record why objects feel hot or cold — because heat flows from them to you or from you to them.
To understand heat, you need to understand thermal energy. Thermal energy is the energy that a body has in the vibrations of its molecules — the energy stored in the internal molecular motion of an object. The temperature of a body usually increases with its thermal energy.
When two bodies are brought into thermal contact, thermal energy is free to be exchanged between them. If no thermal energy flows between them, they are in thermal equilibrium. In other words, they are in a kind of balance. Two objects in thermal equilibrium are said to have the same temperature. If thermal energy does flow between them — an object at a higher temperature is in thermal contact with an object at a lower temperature and the thermal energy flows from the hotter body to the cooler one — they are not in thermal equilibrium.
This section covers heat and how the change in energy affects temperature. I also discuss phase changes, special cases in which a substance can absorb heat without changing temperature.
Getting specific with temperature changes
Suppose you see someone making a pot of coffee. You measure exactly 1.0 kilogram of brewed coffee in the pot, and then you get down to the real measurements. You find out that you need 4,186 joules of heat energy to raise the temperature of the coffee by 1°C, but you need only 840 joules to raise 1.0 kilogram of glass by 1°C; the coffee and glass have different specific heat capacities. The energy goes into the substance being heated, which stores the energy as internal energy until it leaks out again. (Note: If you need 4,186 joules to raise 1.0 kilogram of coffee by 1°C, you need double that, 8,372 joules, to raise 2.0 kilograms of coffee by 1°C or to raise 1.0 kilogram of coffee by 2°C.)
Q = cmΔT
Here, Q is the amount of heat energy involved (measured in joules if you’re using the MKS system), m is the mass, ΔT is the change in temperature, and c is a constant called the specific heat capacity, which is measured in joules per kilogram-degree Celsius, or J/(kg·°C). In Chapter 16, you can find a calculation of the specific heat capacity for the special case of an ideal gas, but usually physicists calculate specific heat capacity through experiment, so most problems give you c or refer you to a table of specific-heat values for various materials.
You can use the heat equation to find out how temperature changes when you mix liquids of different temperatures. Suppose you have 45 grams of coffee in your cup, but it cooled while you were figuring out the coffee’s specific heat. You call over your host. The coffee is 45°C, but you like it at 65°C. The host gets up to pour some more. “Just a minute,” you say. “The coffee in the pot is 95°C. Wait until I calculate exactly how much you need to pour.”
The following equation represents the heat lost by the new mass of coffee, m1:
ΔQ1 = cm1(T – T1,0)
And here’s the heat gained by the existing coffee, mass m2:
ΔQ2 = cm2(T – T2,0)
Assuming you have a superinsulating coffee mug, no energy leaves the system to the outside, and because energy cannot be created or destroyed, energy is conserved within such a closed system; therefore, the heat lost by the new coffee is the heat that the existing coffee gains, so
ΔQ1 = –ΔQ2
Therefore, you can say the following:
cm1(T – T1,0) = –cm2(T – T2,0)
Dividing both sides by the specific heat capacity, c, and plugging in the numbers gives you the following:
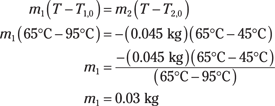
You need 0.03 kilograms, or 30 grams. Satisfied, you put away your calculator and say, “Give me exactly 30 grams of that coffee.”
Just a new phase: Adding heat without changing temperature
Imagine you’re calmly drinking your lemonade at an outdoor garden party. You grab some ice to cool your lemonade, and the mixture in your glass is now half ice, half lemonade (which you can assume has the same specific heat as water), with a temperature of exactly 0°C.
As you hold the glass and watch the action, the ice begins to melt — but the contents of the glass don’t change temperature. Why? The heat (thermal energy) going into the glass from the outside air is melting the ice, not warming the mixture up. So does this make the equation for heat energy (Q = cmΔT) useless? Not at all — it just means that the equation doesn’t apply for a phase change.
In this section, you see how heat affects temperature before, during, and after phase changes.
Breaking the ice with phase-change graphs
If you graph the heat added to a system versus the system’s temperature, the graph usually slopes upward; adding heat increases temperature. However, the graph levels out during phase changes, because on a molecular level, making a substance change state requires energy. After all the material has changed state, the temperature can rise again.
Imagine that someone has taken a bag of ice and thoughtlessly put it on the stove. Before it hit the stove, the ice was at a temperature below freezing (–5°C), but being on the stove is about to change that. You can see the change taking place in graph form in Figure 14-2.
As long as no phase change takes place, the equation Q = cmΔT holds (the specific heat capacity of ice is around 2.0 × 10–3 J/kg∙°C), which means that the temperature of the ice will increase linearly as you add more heat to it, as you see in the graph.
However, when the ice reaches 0°C, the ice is getting too warm to hold its solid state, and it begins to melt, undergoing a phase change. When you melt ice, breaking up the crystalline ice structure requires energy, and the energy needed to melt the ice is supplied as heat. That’s why the graph in Figure 14-2 levels off in the middle — the ice is melting. You need heat to make the ice change phase to water, so even though the stove adds heat, the temperature of the ice doesn’t change as it melts.
Figure 14-2: Phase changes of water.
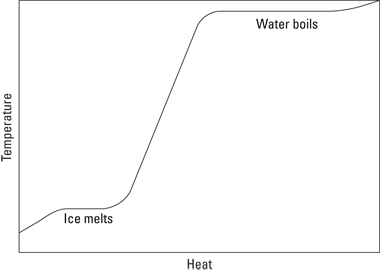
As you watch the bag of ice on the stove, however, you note that all the ice eventually melts into water. Because the stove is still adding heat, the temperature begins to rise, which you see in Figure 14-2. The stove adds more and more heat to the water, and in time, the water starts to bubble. “Aha,” you think. “Another phase change.” And you’re right: The water is boiling and becoming steam. The bag holding the ice seems pretty resilient, and it expands while the water turns to steam.
You measure the temperature of the water. Fascinating — although the water boils, turning into steam, the temperature doesn’t change. Once again, you need to add heat to incite a phase change — this time from water to steam. You can see in Figure 14-2 that as you add heat, the water boils, but the temperature of that water doesn’t change.
What’s going to happen next, as the bag swells to an enormous volume? You never get to find out, because the bag finally explodes. You pick up a few shreds of the bag and examine them closely. How can you account for the heat that’s needed to change the state of an object? How can you add something to the equation for heat energy to take into account phase changes? That’s where the idea of latent heat comes in.
Understanding latent heat
Latent heat is the heat per kilogram that you have to add or remove to make an object change its state; in other words, latent heat is the heat needed to make a phase change happen. Its units are joules per kilogram (J/kg) in the MKS system.
 The latent heat of fusion, Lf: The heat per kilogram needed to make the change between the solid and liquid phases, as when water turns to ice or ice turns to water
The latent heat of fusion, Lf: The heat per kilogram needed to make the change between the solid and liquid phases, as when water turns to ice or ice turns to water
 The latent heat of vaporization, Lv: The heat per kilogram needed to make the change between the liquid and gas phases, as when water boils or when steam condenses into water
The latent heat of vaporization, Lv: The heat per kilogram needed to make the change between the liquid and gas phases, as when water boils or when steam condenses into water
 The latent heat of sublimation, Ls: The heat per kilogram needed to make the change between the solid and gas phases, as when dry ice evaporates
The latent heat of sublimation, Ls: The heat per kilogram needed to make the change between the solid and gas phases, as when dry ice evaporates
Water’s latent heat of fusion of water, Lf, is 3.35 × 105 J/kg, and its latent heat of vaporization, Lv, is 2.26 × 106 J/kg. In other words, you need 3.35 × 105 joules to melt 1 kilogram of ice at 0°C (just to melt it, not to change its temperature). And you need 2.26 × 106 joules to boil 1 kilogram of water into steam.
ΔQ = mL
Here, L takes the place of the ΔT (change in temperature) and c (specific heat capacity) terms in the temperature-change formula.
Suppose you’re in a restaurant with a glass of 100.0 grams of water at room temperature, 25°C, but you’d prefer ice water at 0°C. How much ice would you need? You can find the answer using the heat formulas for both change in temperature and phase change.
You get out your clipboard, reasoning that the heat absorbed by the melting ice must equal the heat lost by the water you want to cool. Here’s the heat lost by the water you’re cooling:
ΔQwater = cmΔT = cm(T – T0)
where ΔQwater is the heat lost by the water, c is the specific heat capacity of water, m is the mass of the water, ΔT is the change in temperature of the water, T is the final temperature, and T0 is the initial temperature.
Plugging in the numbers tells you how much heat the water needs to lose:
ΔQwater = cm(T – T0)
= (4,186 J kg–1 K–1)(0.100 kg)(0 K – 25 K) ≈ –1.04 × 104 J
Therefore, the water needs to lose 1.04 × 104 joules of heat.
So how much ice would that amount of heat melt? That is, how much ice at 0°C would you need to add to cool the water to 0°C? That would be the following amount, where Lf is the latent heat of fusion for ice:
ΔQice = miceLf
For ice, Lm is 3.35 × 105 J/kg, so you get this answer:
ΔQice = mice(3.35 × 105 J/kg)
You know this has to be equal to the heat lost by the water, so you can set this equal and opposite to ΔQwater, or –1.04 × 104 joules:
ΔQice = –ΔQwater
mice(3.35 × 105 J/kg) = –(–1.04 × 104 J)
In other words,
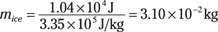
So you need 3.10 × 10–2 kilograms, or 31.0 grams of ice.
“Pardon me,” you say to the waiter. “Please bring me exactly 31.0 grams of ice at precisely 0°C.”


