Chapter 15

Here, Take My Coat: How Heat Is Transferred

In This Chapter

Examining natural and forced convection

Transferring heat through conduction

Shining the light on radiation

Heat is the flow of thermal energy from one point to another (see Chapter 14). You witness the transfer of heat every day. You cook some pasta, and you see currents of water cycling the noodles in the pan. You pick up the pan without a hand towel, and you burn your hand. You look to the sky on a summer day, and you feel your face warming up. You give your coat to your date, and you watch his or her feelings for you warm up (through radiation, of course!).

In this chapter, I discuss the three primary ways in which heat can be transferred. You find out how to predict how quickly pot handles get hot, see why heat rises, and discover how the sun warms the Earth.

Convection: Letting the Heat Flow

Convection is a means of transferring thermal energy (heat) in a fluid. In convection, the flowing fluid carries energy along, mixing with the rest of the fluid and thereby transferring the thermal energy. Through this mixing, thermal energy moves from a higher-temperature region to a lower-temperature region.

Convection occurs in both liquids and gases, because both liquids and gases are fluids. Buoyancy, which is the upward force on the part of the fluid that’s less dense than the surrounding fluid, often drives the fluid’s motion. Fluids expand when you add heat, changing the fluid’s density (refer to Chapter 14 for info on thermal expansion). Cooler, denser regions of fluid tend to sink as warmer, less dense regions rise, causing the fluid to flow.

Figure 15-1 shows a cross-section of a pan of water coming to the boil. The water at the bottom heats up, expands slightly, and then rises in the pan by buoyant forces. The warm fluid carries the thermal energy from the bottom of the pan to the top.

Figure 15-1: You can see convection in action by boiling a pot of water.

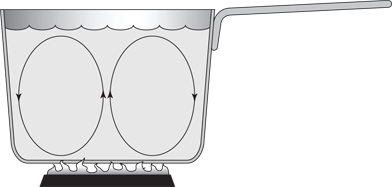
Convection may be natural or forced, and the following subsections give you the story on both.

Hot fluid rises: Putting fluid in motion with natural convection

You may have heard the maxim “heat rises,” which is all about convection. However, a more accurate statement is that “hot fluid rises.” In substances where convection is free to take place — that is, in gases and liquids — hotter material naturally ends up on top and cooler material ends up on the bottom because of buoyancy.

If your house has two floors, you often end up with the bottom floor being cooler than the top floor. The warmer air rises by buoyancy, which drives the convection. Physicists refer to this type of convection as natural convection because it isn’t externally driven.

To understand how natural convection works, look at the microscopic picture. Any substance is made up of molecules, tiny particles that zip around at varying speeds. When a gas or liquid becomes hot, its molecules move faster. If you have a heating element that contacts the bottom of the substance — such as a wood stove at the bottom of a room or a stove element that’s heating a kettle of water — the molecules near the heating element become hot. Hotter molecules have more kinetic energy and so can zip around faster and hit other molecules harder.

Because they move faster and hit harder, hotter molecules make the substance in their immediate area less dense. That is, they have more energy with which to push other molecules out of the way. The molecules that have been hit also have more energy to push other molecules out of the way, so the substance in the immediate vicinity of the heating element becomes less dense.

A unit volume of material that’s less dense weighs less than a unit volume of the surrounding material, and if that material is a gas or liquid, the less dense stuff rises. Because the denser material has more mass per volume, it sinks under the influence of gravity.

Anyone who has ever flown in a plane is familiar with natural convection in the form of turbulence. Turbulence is caused by the sun’s heating of the Earth, which in turn heats the air above it. The hot air rises through the atmosphere, and airplanes, going along on their merry way, fly through these rising columns of rising hot air. If you look out the window of the plane, you may see birds riding these columns, called thermals, as well. If you see a bird rising but not flapping its wings, it’s most likely hitching a ride on a thermal.

Controlling the flow with forced convection

With natural convection, you rely on the fact that hot fluid rises to transfer heat. But sometimes natural convection is the opposite of what you want. With forced convection, you control the movement of the warm or cool fluid, often using a fan or pump.

For example, take a room on a cold winter’s day. Because heat rises, the hotter air in the room drifts up to the ceiling, while the cooler air in the room settles near the bottom of the room, where you are. So in time, all the hot air in the room collects near the ceiling, and all the cold air collects near the floor. Although you were originally quite cozy, you may now be getting pretty cold — all as a result of natural convection.

What can you do? You can turn on your room’s ceiling fan in reverse! Ceiling fans force the air to circulate, so the hot air near the top of the room moves downward. The warmer air at the top of the room now ends up at the bottom of the room again, where you are. Just make sure you choose a low speed so you don’t create a breeze.

You find forced convection all around you. The fans in a desktop computer, for example, cause forced convection (and the lack of room for a fan in laptop computers has caused plenty of overheating problems). Refrigerators use fans to blow away heat, again relying on forced convection.

Natural convection is the dominant way heat is transferred through the interior of any standard oven (microwave ovens, on the other hand, use electromagnetic radiation to jostle the water molecules in the food — see Chapter 19 for details). In traditional ovens, the buoyancy of the hot air distributes the heat. Ovens specifically labeled convection ovens use a fan to increase the heat transfer by convection. The fan drives the air inside the oven to move more and thereby distribute the heat faster.

Here’s a last example, this time of forced convection happening twice in the same system. Cars generate a lot of heat when they’re running. To keep the engine cool, a pump circulates coolant throughout the engine. The liquid coolant transfers heat away from the engine to the radiator to keep the car from overheating. And the radiator itself is another example of forced convection, moving the air not with a cooling fan but with the motion of the car itself: the car drives air through the radiator, cooling it as the car moves. When the car isn’t moving, the engine produces less heat, so there’s less need to dissipate heat from the radiator.

Too Hot to Handle: Getting in Touch with Conduction

Conduction transfers heat through material directly, through contact. Take a look at the metal pot in Figure 15-2 and its metal handle; the pot has been boiling for 15 minutes. Would you want to lift it off the fire by grabbing the handle without an oven mitt? Probably not. The handle is hot because of conduction of heat through the metal handle.

On the molecular level, the molecules near the heat source are heated and begin vibrating faster. They bounce off nearby molecules and cause them to vibrate faster. That increased bouncing is what heats a substance.

Figure 15-2: Conduction heats the pot that holds the boiling water.

How the elephant got its ears: A physics lesson in body design

As bodies become larger, their volume grows faster than their surface area. Cooling a larger body becomes more difficult because for every unit of volume of the body, there’s less surface area through which the heat can escape. This idea also applies to animals, and it partly explains why the elephant needs such large ears. Because an elephant has such a large body, it has lots of heat to conduct through its body and then from its skin to the air; but relative to its large volume, the elephant doesn’t have much surface area through which to conduct the heat. So the elephant sports two great big ears, with a large surface area, through which to conduct away its heat.

Some materials, such as most metals, conduct heat better than others, such as porcelain, wood, or glass. The way substances conduct heat depends a great degree on their molecular structures, so different substances react differently.

Finding the conduction equation

You have to take different properties of objects into account when you want to examine the conduction that takes place. If you have a bar of steel, for example, you have to consider the bar’s area and length, along with the temperature at different parts of the bar.

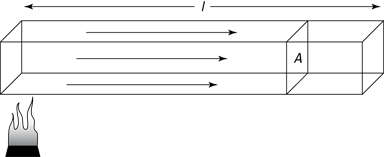
Take a look at Figure 15-3, where a bar of steel is being heated on one end and the heat is traveling by conduction toward the other side. Can you find out the thermal energy transferred? No problem.

Here are the factors that affect the rate of conduction:

Temperature difference: The greater the difference in temperature between the two ends of the bar, the greater the rate of thermal energy transfer, so more heat is transferred. The heat, Q, is proportional to the difference in temperature, ΔT:

Q ΔT

Cross-sectional area: A bar twice as wide conducts twice the amount of heat. In general, the amount of heat conducted, Q, is proportional to the cross-sectional area, A, like this:

Q A

Length (distance heat must travel): The longer the bar, the less heat that will make it all the way through. Therefore, the conducted heat is inversely proportional to the length of the bar, l:

Time: The amount of heat transferred, Q, depends on the amount of time that passes, t — twice the time, twice the heat. Here’s how you express this idea mathematically:

Q t

Figure 15-3: Conducting heat in a bar of steel.

Now you can put the variables together, using k as a constant of proportionality that’s yet to be determined.

Here’s the equation for heat transfer by conduction through a material:

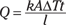
This equation represents the amount of heat transferred by conduction in a given amount of time, t, down a length l, where the cross-sectional area is A. Here, k is the material’s thermal conductivity, measured in joules per second-meters-degrees Celsius, or J/s·m·°C.

Working with thermal conductivity

Different materials (such as glass, steel, copper, and bubble gum) conduct heat at different rates, so the thermal conductivity constant depends on the material in question. Lucky for you, physicists have measured the constants for various materials already. Check out some of the values in Table 15-1.

Table 15-1 Thermal Conductivities for Various Materials

Material	Thermal Conductivity (J/s·m·°C)
Diamond	1,600
Silver	420
Copper	390
Brass	110
Lead	35
Steel	14.0
Glass	0.80
Water	0.60
Body fat	0.20
Wood	0.15
Wool	0.04
Air	0.0256
Styrofoam	0.01

The thermal conductivity of the steel part of a pot handle is 14.0 J/s·m·°C (see Table 15-1). Take a look at Figure 15-3. Suppose the handle is 15 centimeters long, with a cross-sectional area of 2.0 square centimeters (2.0 × 10–4 m2). If the fire at one end is 600°C, how much heat would be pumped into your hand in 1 second if you grabbed the handle? The equation for heat transfer by conduction is

If you assume that the end of the cool end of the handle starts at about room temperature, 25°C, you get the following amount of heat transferred in a time t:

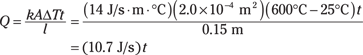
You can see that in 1 second, 10.7 joules of thermal energy would enter your hand.

If 10.7 joules of heat is being transferred to the end of the handle each second, then the heat transfer is 10.7 joules per second, or 10.7 watts. As the seconds go by, the joules of heat add up, making the handle hotter and hotter. Note that the conduction rate of 10.7 watts will decrease with time because the end of the handle heats up, giving you a smaller value for ΔT.

Camping with the Johnsons: A conduction example

The vacationing Johnson family wants to know whether they have enough ice in their ice chest to last for 12 hours while they’re out camping, so they ask you, the famous consulting physicist. A quick glance at your outdoor thermometer tells you that the outside temperature is 35°C. You measure the walls of the Styrofoam ice chest to be 2.0 centimeters thick. The total surface area of the ice chest is 0.66 square meters.

The final measurement you note on your clipboard is that the Johnsons have loaded the ice chest with exactly 1.5 kilograms of ice at 0°C. So how long will 1.5 kilograms of ice take to melt in that chest?

Because, in this situation, you have an amount of heat conducting through a material of known surface area and thickness, you can start with the conduction equation:

You want to know the time, so solve the equation for t:

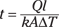
Now think about which values you already know. The heat has to travel the width of the cooler to escape, so l = 2.0 cm = 0.020 m. Styrofoam’s thermal conductivity is k = 0.010 J/s·m·°C, and the ice chest’s surface area is A = 0.66 m2. The difference between inside and outside temperature is ΔT = 35°C – 0°C = 35°C. Now all you need is Q, the amount of heat needed to melt the ice.

You can use water’s latent heat of fusion to figure out how much heat you need to change the ice from a solid to liquid state (see Chapter 14 for details on heat and phase changes). In general, you need the following amount of heat to melt ice at 0°C:

Q = mL

where Q is the amount of heat needed, m is the mass of ice, and L is water’s latent heat of fusion, 3.35 × 105 J/kg. Plugging in the numbers gives you the amount of heat you need:

Q = mL = (1.5 kg)(3.35 × 105 J/kg) ≈ 5.0 × 105 J

Now you know Q, so you have enough info to use the conduction equation. Plugging the numbers in the conduction equation (solved for time) gives you the answer:

You tell the Johnsons, “It will take 44,000 seconds for your ice to melt.”

“How long is that?” they ask.

Well, you think, 60 seconds are in a minute, and 60 minutes are in an hour, so you do a few more calculations:

“Your ice will last for 12 hours,” you tell them, handing them your bill.

Considering conductors and insulators

Materials with high thermal conductivity, such as copper, conduct heat well. For example, you may have seen copper wire in indoor/outdoor thermometers. The wires conduct heat in from outside so that the thermometer can measure the outside temperature. Diamond is a far better conductor of heat than copper, as you can see in Table 15-1 (but building indoor/outdoor thermometers with diamonds would be a little pricey).

On the other end of the scale, some materials act as heat insulators because their thermal conductivity is so low. For example, body fat has a low thermal conductivity, as you can see in Table 15-1, and so it’s a natural insulator. Thus, body fat can help keep you warm on cold days.

Of course, in terms of conduction, the champion thermal insulator of all time is a vacuum. Conduction relies on the movement of heat through material, and if there’s no material, there can’t be any conduction. Nothing can conduct the heat in that case.

For that reason, people use vacuum flasks to keep foods hot or cold. These flasks have a double wall with a vacuum between the walls, so no heat can be conducted from inside to outside or outside to inside. Therefore, your soup stays hot, or your iced tea stays cold.

Cool to the touch

Why do metals feel cold to the touch when they’re at room temperature? If you know something about thermal conduction, the phenomenon makes sense. Metals are such good thermal conductors that they carry away the heat from your fingers very quickly, which leads to a drop in temperature in your skin. The nerves in your skin detect this drop in temperature and send the message to your brain that you’re touching something cold. Wood, on the other hand, is not a good conductor (it’s an insulator), so little heat is conducted away from your fingertips. Your brain interprets this to mean that the wood is warmer than the metal, when they’re actually both in thermal equilibrium with the room — that is, the same temperature!

Some thermal conductivity does exist between inside and outside in a vacuum flask. There’s always some path for heat to take, such as the stopper of the flask itself. Because some heat is conducted, vacuum flasks keep hot foot hot or cold food cold only for a little while. Theoretically, if you had a capsule of food floating in a vacuum, there’d be no heat loss or gain through conduction at all — but there’d still be heat loss or gain through radiation.

Radiation: Riding the (Electromagnetic) Wave

Radiation is another way to transfer heat. You experience radiation personally whenever you get out of the shower soaking wet in the dead of winter and bask in the warmth of the heat lamp in your bathroom. Why? Because of a little physics, of course. The heat lamp, which you see in Figure 15-4, beams out heat to you and keeps you warm through radiation.

With radiation, electromagnetic waves carry the energy (you can find plenty of info on electromagnetic waves in Physics II For Dummies). Electromagnetic radiation comes from accelerating electric charges. On a molecular level, that’s what happens as objects warm up — their molecules move around faster and faster and bounce off other molecules hard.

Heat energy transferred through radiation is as familiar as the light of day; in fact, it is the light of day. The sun is a huge thermal reactor about 93 million miles away in space, and neither conduction nor convection can produce any of the energy that arrives to Earth through the vacuum of space. The sun’s energy gets to the Earth through radiation, which you can confirm on a sunny day just by standing outside and letting the sun’s rays warm your face.

Figure 15-4: An incandescent light bulb radiates heat into its environment.

Mutual radiation: Giving and receiving heat

Every object around you is continually radiating, unless its temperature is at absolute zero (which is a little unlikely because you can’t physically get to a temperature of absolute zero, with no molecular movement). A scoop of ice cream, for example, radiates. Even you radiate all the time, but that radiation isn’t visible as light because it’s in the infrared part of the spectrum. However, that light is visible to infrared scopes, as you’ve probably seen in the movies or on television.

You radiate heat in all directions all the time, and everything in your environment radiates heat back to you. When you have the same temperature as your surroundings, you radiate as fast and as much to your environment as it does to you. When two things are in thermal contact but no thermal energy is exchanged between them, they’re in thermal equilibrium. If two things are in thermal equilibrium, they have the same temperature.

If your environment didn’t radiate heat back to you, you’d freeze, which is why space is considered so “cold.” There’s nothing cold to touch in space, and you don’t lose heat through conduction or convection. Rather, the environment doesn’t radiate back at you, which means that the heat you radiate away is lost. You can freeze very fast from the lost heat.

When an object heats up to about 1,000 kelvins, it starts to glow red (which may explain why, even though you’re radiating, you don’t glow red in the visible light spectrum). As the object gets hotter, its radiation moves up in the spectrum through orange, yellow, and so on up to white hot at somewhere around 1,700 K (about 2,600°F).

Radiant heaters with coils that glow red rely on radiation to transfer heat. Convection takes place as air heats, rises, and spreads around the room (and conduction can occur if you touch the heater on a hot spot by mistake — not the most desirable of heat transfers!). But the heat transfer to you takes place mostly through radiation.

Blackbodies: Absorbing and reflecting radiation

Humans understand heat radiation and absorption in the environment intuitively. For example, on a hot day, you may avoid wearing a black t-shirt, because you know it would make you hotter. A black t-shirt absorbs light from the environment while reflecting less of it back than a white t-shirt. The white t-shirt keeps you cooler because it reflects more radiant heat back to the environment.

Some objects absorb more of the light that hits them than others. Objects that absorb all the radiant energy that strikes them are called blackbodies. A blackbody absorbs 100 percent of the radiant energy striking it, and if it’s in equilibrium with its surroundings, it emits all the radiant energy as well.

In terms of reflection and absorption of radiation, most objects fall somewhere between mirrors, which reflect almost all light, and blackbodies, which absorb all light. The middle-of-the-road objects absorb some of the light striking them and emit it back into their surroundings. Shiny objects are shiny because they reflect most of the light, which means they don’t have to emit as much heat radiantly into the room as other objects. Dark objects appear dark because they don’t reflect much light, which means they have to emit more as radiant heat (usually lower down in the spectrum, where the radiation is infrared and can’t be seen).

The Stefan-Boltzmann constant

How much heat does a blackbody emit when it’s at a certain temperature? The amount of heat radiated is proportional to the time you allow — twice as long, twice as much heat radiated, for example. So you can write the heat relation, where t is time, as follows:

Q t

And as you may expect, the amount of heat radiated is proportional to the total area doing the radiating. So you can also write the relation as follows, where A is the area doing the radiating:

Q At

Temperature, T, has to be in the equation somewhere — the hotter an object, the more heat radiated. Experimentally, physicists found that the amount of heat radiated is proportional to T to the fourth power, T4. So now you have the following relation:

Q AtT4

To show the exact relationship between heat and the other variables, you need to include a constant, which physicists measured experimentally. To find the heat emitted by a blackbody, you use the Stefan-Boltzmann constant, σ, which goes in the equation like this:

Q = σAtT4

The value of σ is 5.67 × 10–8 J/s·m2·K4. Note, however, that this constant works only for blackbodies that are perfect emitters.

The Stefan-Boltzmann law of radiation

Most objects aren’t perfect emitters, so you have to add another constant most of the time — one that depends on the substance you’re working with. The constant is called emissivity, e.

The Stefan-Boltzmann law of radiation says the following:

Q = eσAtT4

where e is an object’s emissivity, σ is the Stefan-Boltzmann constant 5.67 × 10–8 J/s·m2·K4, A is the radiating area, t is time, and T is the temperature in kelvins.

Finding heat from the human body

A person’s emissivity is about 0.98. At a body temperature of 37°C, how much heat does a person radiate each second? First, you have to factor in how much area does the radiating. If you know that the surface area of the human body is A = 1.7 m2, you can find the total heat radiated by a person by plugging the numbers into the Stefan-Boltzmann law of radiation equation, making sure you convert the temperature to kelvins:

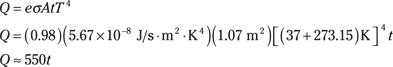
Then dividing both sides by t, you get

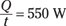
You get a value of 550 joules per second, or 550 watts. That may seem high, because skin temperature isn’t the same as internal body temperature, but it’s in the ballpark.

Doing star calculations

Here’s another example: A knock sounds on your door at around 10 p.m. Surprised, you open the door, and a number of astronomers enter. “We need you to measure the radius of Betelgeuse,” they say.

“Betelgeuse, the star?” you ask. “You want me to measure the radius of a star 640 light-years from Earth?”

“If it’s not too much trouble,” they reply. “We heard it was a supergiant star, and we wanted to know how big it was.”

You get out your telescope and find Betelgeuse. Using the set of instruments you always carry in your pocket, you use the spectrum of the star to measure its temperature (the distribution of the intensity of the light over the different wavelengths is directly related to its surface temperature because stars radiate like blackbodies). The temperature is about 2,900 kelvins and the star’s power output is 4.0 × 1030 watts.

Because you know the rate at which the star is radiating energy and its surface temperature, you can use the Stefan-Boltzman law of radiation to relate the star’s surface area to these known values. Then assuming the star is a sphere, you can easily work out the radius of the sphere that has that surface area.

You know that Q = eσAtT4, so the power is

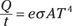
And you can solve for the surface area of the star, A, like this:

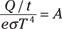
Assuming that Betelgeuse is a sphere, you can connect the surface area to the star’s radius by using this formula for spheres:

A = 4πr2

Solve for r:

Plugging in the star’s surface-area expression for A, you get the following:

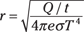
Assuming that e = 1, plugging in numbers gives you:

That’s a pretty big radius for a star. If the sun had that radius, the Earth would be inside it — and so would Mars.

“Two hundred eighty million kilometers,” you tell the astronomers, and you hand them your bill.