What’s the difference between a ground ball and a fly ball? Between the motion of a basketball during a free throw and a ball being dribbled? Or the path of a skateboard down the street and the path of one on a ramp? They all have different trajectories.
A trajectory is the path an object takes as it moves. A rolling ball has a straight trajectory because it moves in one direction. A dribbled basketball also has a straight trajectory because it moves only up and down. A ground ball is an example of horizontal motion. Horizontal motion can be left or right, forward or backward—any motion that isn’t up or down. A dribbled basketball has vertical motion, which is motion that is only up or down.
ESSENTIAL QUESTION
When might it be useful to know the height and distance a projectile has traveled?
WORDS TO KNOW
trajectory: the curve a body travels along in its path through space.
horizontal: straight across from side to side.
vertical: straight up and down.
ballistic trajectory: the trajectory of an object acted upon by only gravity and air resistance.
Projectiles don’t follow straight trajectories. They fly over fields and fall into gloves or beyond outfield walls. They sail through the air, hitting the bulls-eye on a target 100 feet away. Projectiles have both horizontal and vertical motion because they are most often launched at angles. Together, they determine whether a ball is a home run or an out, or if an arrow hits the bulls-eye or misses the target.
DID YOU KNOW?
Can you think of objects that move only vertically? What about things that move only horizontally?
BALLISTIC MOTION
When it comes to ballistics and the motion of projectiles, gravity is (almost) everything. When you throw a ball into the air, you apply a force to the ball to send it on its way. But once the ball leaves your hand, you’re no longer applying a force. According to Newton’s first law, the ball should keep moving in a straight line at the same speed. But does it?
As soon as the ball leaves your hand, the only force acting on it is gravity. This is the same for bullets, baseballs, arrows, and bombs. When the only force acting on a projectile is gravity, it has ballistic motion. Gravity is always pulling projectiles downward, curving their paths into a ballistic trajectory.
What force will act on this baseball once it leaves the pitcher’s hand?
parabola: an upside down, U-shaped curve that is a cross section of a cone.
rate: the speed of something measured in an amount of time, such as miles per hour or feet per second.
lofted: an object that is propelled up.
The shape of a ballistic trajectory is called a parabola. Parabolas can be tall, such as the path of a punted football, or they can be almost flat, such as the path of a bullet.
Parabolas are the result of two kinds of motion: horizontal motion and vertical motion.
When studying ballistics, it’s helpful to look at horizontal and vertical motion separately to understand how they affect the motion of projectiles.
Powerful Parabolas
Have you seen a parabola? Parabolas aren’t just found in the motions of projectiles. The mirrors inside car headlights are shaped like parabolas, helping to illuminate roads at night. Parabolas are also used in bridges to make them lighter and stronger. Where else do you see this mighty shape? Want to see a parabola in action? Water follows a parabolic path, too! If you have a squirt gun or a hose, you can watch the water fall to the ground on a ballistic trajectory!
You’ve seen horizontal motion in action. When a ball rolls across a room or when you slide in your socks on a slippery floor, that’s horizontal motion. Forward, backward, or side-to-side, horizontal motion is everywhere. Because it’s easy to move horizontally, it’s easy to calculate the rate, or speed, of an object when it’s moving!
Horizontal motion shows us how Newton’s first law of motion works. When a ball is moving, it will keep moving at the same speed and in the same direction until another force comes along to change its velocity.
Unless the ball runs into a wall or your shoe, friction will be the force that slows and stops the ball.
But what about a lofted soccer ball or an arrow? A projectile has horizontal motion, but without friction between itself and the ground, it should continue with the same horizontal speed and direction forever, according to the first law. But that doesn’t happen!
Friction Facts
There are two basic types of friction. Static friction occurs when something rests on a surface, such as your shoes on the pavement or a car parked on the street. Kinetic friction happens between objects that are moving against each other. A sled sliding across snow or a ball rolling along the ground are examples of kinetic friction.
A projectile’s horizontal velocity does stay the same until something stops it, such as a fielder’s glove or a wall. It’s the vertical motion of the projectile that brings an arrow’s flight to an end and brings even the hardest hit ball back to Earth. What goes up, must come down—thanks to the vertical motion caused by gravity.
normal force: the support force pushing upward on an object from the ground.
angle: the space between two lines that start from the same point, measured in degrees.
VERTICAL MOTION
When you dribble a basketball or ride an elevator, you are experiencing vertical motion. Newton’s first law should work for something that’s moving horizontally or vertically. But you don’t need to apply a force to make your tablet or a book fall. You just need to drop it.
DID YOU KNOW?
Basketball players often have their vertical leap measured. It tells them how high they can jump! What is your vertical leap?
When you drop something, Newton’s first law says that it should stay right where it is. After all, you’re not pushing it up or down, so you’re not applying a force, right?
But that’s not what happens. As soon as you let go, an object falls until something stops it—usually the ground. That’s because the force of gravity accelerates anything you drop as soon as you let go.
In fact, just by holding it, you are applying a force to keep the object from falling. This force is called the normal force. When you sit in a chair, gravity tries to make you fall by accelerating you downward. But the chair stops that from happening.
Gravity is the action force, and the chair applies the normal force, which is the reaction force!
Thanks to Galileo’s experiment, we know that gravity accelerates everything equally. It doesn’t matter how much mass an object has—a piano falls at the same rate as a pickle. But knowing just how much gravity accelerates something can help us understand projectile motion!
No matter how an object is moving, the force of gravity is always causing an acceleration toward the center of the earth, even if you throw a ball straight up. If you toss a ball straight up, gravity decelerates the ball, slowing its speed until it starts to fall back to the earth.
|
|
But objects such as basketballs and rockets don’t move only up and down. If they did, they’d be much less interesting! A baseball hit to the outfield can be a home run only if it travels far and high enough to fly over the fence.
To become a home run, a well-struck baseball needs to combine vertical and horizontal motion. To do that, the ball must be hit at an angle.
independent: not influenced or affected by other things.
free fall: when gravity is the only force acting on a moving object.
maximum height: when gravity slows the vertical velocity of a projectile to zero so it is neither rising nor falling.
When a projectile is launched at an angle, it has vertical motion and horizontal motion. An arrow has horizontal motion toward its target, and gravity accelerates its vertical motion.
So, are vertical and horizontal motion independent of each other, or does one affect the other?
THE DROP TEST
Imagine a coin shot horizontally from a slingshot. At the same time, a coin is dropped from the same height as the slingshot without any horizontal motion. Does Galileo’s experiment still work? Are vertical and horizontal velocity independent or does one kind of motion affect the other?
A Delta II rocket launches at an angle and arcs across the night sky. Can you spot the parabola? What kinds of motions are displayed here?
credit: NASA/Bill Ingalls
Falling things such as a dropped microphone or a plummeting skydiver are sometimes said to be in free fall. Free fall occurs when gravity is the only force acting on a moving object.
You might think that the coin with horizontal motion would take longer to hit the ground, because it has a greater distance to travel.
But both coins still hit the ground at the same time! That’s because horizontal and vertical motion really are independent, or separate, from each other.
Even a bullet fired from a gun would hit the ground at the same time as a bullet dropped from the same height! And when a projectile is fired at an angle, its horizontal velocity stays the same during its flight, but its vertical velocity is always changing.
Gravity doesn’t care if a projectile has horizontal motion or not, it pulls on everything the same way. Knowing that the horizontal and vertical motions of projectiles are independent is very helpful, because it lets us figure out some interesting things about a projectile’s ballistic motion.
HOW HIGH CAN YOU THROW?
Imagine a long fly ball hit into the outfield. At the beginning of its flight, the ball is rising into the air. But gravity is pulling on it, slowing its vertical motion until, for a brief instant, the ball isn’t rising or falling. This is the projectile’s maximum height! From there, gravity continues to accelerate the ball downward until it hits the ground or lands in a fielder’s glove.
How high did the ball go? Since we know the acceleration of gravity, we can use this information and the time it takes the ball to fall from the top of its parabola to find out its maximum height.
variable: a symbol that holds the place for information that may change.
range: the distance a projectile travels horizontally.
We can use a little math to figure it out with an equation: h = ½g × t2
•h = height of the ball, in feet
•g = acceleration due to gravity, which is 32.2 feet per second, per second
•t = time the ball takes to fall from its maximum height to the ground, in seconds
This math might seem difficult, but you can do it! Let’s say that the ball is in the air for 6 seconds. That means it took 3 seconds to go up and 3 seconds to come back down. How high did the ball go?
•First, multiply the times t, by itself:
3 × 3 = 9
•Next, multiply your result by g (which is 32.2):
9 × 32.2 = 289.8
•Finally, divide your result by two to get h, the height of the ball:
289.8 ÷ 2 = 144.9
If a ball is in the air for 6 seconds, then it reached a height of about 145 feet! You can figure this for any projectile. All you need to know is how long it stayed in the air! That’s because Earth’s gravity always accelerates things at the same rate!
By learning how to do the kind of equations that relate to how projectiles fly, you can figure out lots of different things, which is useful when you enter an archery contest or join a basketball team. While you might not pause the game to figure out the trajectory of the basketball, if you’ve already done your homework, you’ve got a better shot at making the shot!
DID YOU KNOW?
When you see a letter such as h or g in an equation, don’t panic! These are called variables. They’re used to hold the places of things we don’t know, or things we’re going find out!
Now that you can find the height of a projectile, can you find out how far it goes? The distance a projectile travels horizontally is called its range. Finding a projectile’s range can be easy—you simply measure it if you have a long enough tape measure. But you also use math to find out how far a baseball or an arrow has traveled if you know two things: how long the projectile is in the air and its horizontal velocity.
|
|
Here is an equation we can use to help find the range of a projectile if we know the horizontal speed and its flight time: d = r × t
•d = horizontal distance, or range, in feet
•r = rate or horizontal velocity, in feet per second
•t = flight time, in seconds
Suppose you kick a soccer ball at an angle, sending it down the field with a horizontal velocity of 10 feet per second. Using a stopwatch, you determine that it was in the air for a total of 8 seconds. How far did it go?
Multiply the horizontal velocity (r) by the flight time (t) to get the distance (d).
10 × 8 = 80
The ball traveled 80 feet!
Flying Long
The longest home run ever recorded was by Joey Meyer (1962– ) of the Denver Zephyrs. His home run was 582 feet. The longest goal in soccer was scored by goalie Asmir Begović (1987– ), who scored from 100.5 yards. What other records would you like to know?
maximum range: the greatest distance a projectile travels horizontally.
parallel: two lines always the same distance apart.
perpendicular: a line at an angle of 90 degrees to another line or surface. The two lines form a corner, called a right angle.
Why does this work? Because a projectile’s horizontal velocity will stay the same unless a force acts to change it—for example, a ball hitting the ground or an arrow striking a target.
|
|
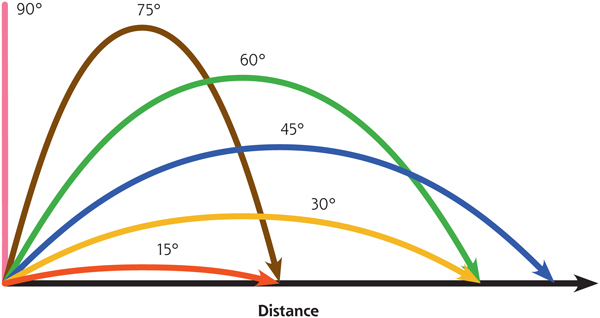
LAUNCH ANGLE
You can calculate the height and range of a projectile using some simple math. But how would you find out the best way to fire a projectile so it travels the greatest distance? This is called maximum range.
A projectile is usually fired at an angle between 0 and 90 degrees, or horizontal and vertical. Horizontal is 0 degrees, or parallel to the ground, and vertical is 90 degrees, or perpendicular to the ground.
Math Practice!
You can calculate the range of a projectile if you know its time in flight and horizontal velocity. Try a few of the problems below. You can draw pictures, create diagrams, make lists—whichever method works best for you! Find the answers on page 118.
›A football is kicked with a horizontal velocity of 22 feet per second and has a flight time of 2 seconds. How far did the football travel?
›A catapult flings a heavy boulder. It takes 5 seconds to reach its target with a horizontal velocity of 20 feet per second. How far away was the target?
›An arrow travels 200 feet. If its horizontal velocity was 50 feet per second, how long did it take to reach its target?
Imagine you’re leading a band of archers against a enemy, and you want to be as far from them as possible when you unleash your attack. Firing straight up isn’t a good idea—the arrows will probably come right back down on the archers themselves. Firing straight ahead won’t work, either. Gravity will pull the arrows to the ground long before they reach the enemy.
To get the greatest range, a projectile should be launched halfway between vertical and horizontal, which is 45 degrees. This way, half of the force acting on the projectile goes toward vertical motion and half goes to horizontal motion. As long as the amount of force between them is the same, you’ll get the greatest range out of your projectiles!
Now that you have a good grasp of the different forces affecting projectiles, let’s look at some of the tools and techniques people have used to send things flying farther and faster!
ESSENTIAL QUESTION
When might it be useful to know the height and distance a projectile has traveled?
FIND THE HORIZONTAL VELOCITY
You can calculate the horizontal velocity of an object if you know how long it takes to go a certain distance. Try it out! You’ll use a tube propped up at an angle to experiment with a rolling ball.
›At one end of a flat table, tape a cardboard tube, such as an empty paper towel roll, to the edge of a stack of books or a small box about 5 or 6 inches high. Tape the other end of the tube to the table. Make sure the tube is as straight as possible.
|
|
›Measure and place a piece of tape 2 feet from the bottom of the tube. Make sure it’s in the path of a ball rolled through the tube.
›Gently place a marble or ball in the tube. Don’t push it! Let it roll!
›Start the timer when the marble hits the table. Stop the timer when the marble crosses the piece of tape. Record your observations in your engineering notebook.
›Do this several times. For each trial, calculate the speed of the ball in feet per second, using the formula for rate (speed):
r = d ÷ t
›Divide the distance (d) by the time (t) to obtain the rate of speed (r).
›Now, calculate the average speed for all the trials. Start by adding up all different rates.
›Divide that total by the number of trials.
›Record your result! This is the average speed of your marble.
Questions to think about
How close are the speeds in each trial?
What things might change the speed of the marble in your experiment?
Why do you think using the tube is better than rolling the marble by hand?
What forces are acting on the marble when it’s in the tube? When it leaves the tube?
If you had a large enough table, how far do you think the marble would roll?
Would a carpet or rug instead of a table change the results of the experiment?
Try This!
Try the experiment again, but this time use a marble or ball of a different mass. Does the mass of the ball affect its speed? Why or why not? Change the steepness of the tube. Does it affect the speed of the ball? Why or why not?
When something falls, the force of gravity is pulling it toward the center of the earth. But how much does gravity accelerate an object when you drop it? Find out by doing some math!
DID YOU KNOW?
Since everything that falls on Earth accelerates at the same rate (32.2 feet per second, per second), physicists use the lowercase “g” to represent the acceleration of gravity. It just makes it easier to work with instead of writing “32.2 feet per second, per second” all the time!
›Choose a height for your drop. This should be at least 3 feet high. Measure carefully! You’ll need to drop objects from the same height each time. Record the height of the drop in your engineering notebook.
›From the height you picked, drop your object. Carefully time—in seconds—how long it takes the object to hit the ground from your measured height.
›Drop the same object at least five times and record how long it takes to hit the ground. Calculate the average drop time in seconds.
›Using the same drop height, try two more objects of different masses. Be sure to record at least five drops for each!
›Calculate the acceleration of gravity following these instructions and record your answer in your engineering notebook!
a = 2d ÷ t2
d = the drop distance (in feet)
t = the average drop time (in seconds)
a = the acceleration due to gravity
Suppose d is 6 feet and t is 4 seconds. Multiply the height of your drop by 2: d × 2. For example, 6 × 2 = 12
Second, multiply the average drop time by itself: t × t. For example, 4 × 4 = 16
Finally, calculate a (acceleration) by dividing the results of the first step by the second step: a = (d × 2) ÷ (t × t). For example, 12 ÷ 16 = 0.75
›Repeat your calculations for the other objects.
›Next, calculate the average acceleration (a). First, add all the values you calculated. Then, divide that sum by the number of experiments you performed. This is how you calculate the acceleration of gravity!
Consider This!
Gravity accelerates everything at a rate of 32.2 feet per second, per second. That means after one second, a dropped book will have a speed of 32.2 feet per second. But because it’s accelerating, the book’s speed is also increasing every second—by 32.2 feet per second! So, after two seconds, it’s moving at a speed of 64.4 seconds, and after three seconds, it’s moving at 96.6 feet per second. That’s about 65 miles per hour!
Questions to think about
Why is it important to do the experiment several times?
Why is using the average important?
Does the acceleration depend on the mass of the object?
What would Galileo have to say about this?
Do you think the results would change if you tried the experiment at a friend’s house? In a different country? On a different planet?
Try This!
Try a different height. Do you get the same results for a? Why or why not? Try using a flat piece of paper, a feather, or other very light object.
GALILEO’S EXPERIMENT, TAKE TWO!
Galileo demonstrated that all objects dropped from the same height accelerate at the same rate and hit the ground at the same time. But what if one object has horizontal motion while the other does not? Will they still reach the ground at the same time?
›If you’re using a video camera, be sure to set it up in a place where the coins can’t damage it.
›Place a ruler at one corner of a table, parallel with one edge of the table. Leave enough space between the ruler and the edge of the table for a coin.
›Place one coin at the end of the ruler. Slide the end with the coin off the table, but don’t let the ruler tip!
›At the other end of the ruler, place another coin on the table. The coin should be between the ruler and the edge of the table, against the ruler and the table’s edge.
›Strike the end of the ruler with the coin that sits on the table. Hit the ruler toward the table’s edge, so that it pushes the coin off the table. You might have to hit the ruler with some force!
›Listen carefully to the sound of the two coins hitting the floor!
›Repeat this several times. Record what you see and hear in your engineering notebook.
Which coin hits the floor first?
What is the difference in the motion of the two coins?
What would happen if the coin that has horizontal motion was launched at an upward angle? Would it change when it hit the ground?
Try This!
Try launching one coin at an angle. Which coin will hit the ground first? How will that affect the motion of the coin? What if one coin is dropped from a different height? Would that change the results of the experiment?
Theory of General Relativity
In 1915, the physicist Albert Einstein (1879–1955) came up with a new way to look at gravity. In his theory of general relativity, Einstein described gravity as distortion in space and time caused by an object’s mass. The more massive something is, the more it can bend space and time! In fact, things with lots of mass, such as stars, can even bend the paths of light from distant stars! And the most massive objects, black holes, have such strong gravity that nothing—not even light—can escape!
|
|
Could you use some hang time? If you know how long a projectile is in the air, you can figure out its maximum height! How high can you get?
›Throw, kick, or launch a projectile! Use something very safe, such as a tennis ball, and launch it in an outdoor space.
›Try launching at several different angles and record what you see. They don’t have to be perfect! You can record “straight up” or “mostly straight up,” for example.
›Have a friend record how long the projectile stays in the air. Start the timer as soon as the projectile starts moving and stop it as soon as it hits the ground. Using a countdown can help!
›Record the result in your engineering notebook. Record several attempts, and then switch places with your friend and repeat the experiment.
›Calculate the height of your projectiles with this formula.
h = ½ g × t2
h = height of the projectile, in feet
g = acceleration due to gravity,
which is 32.2 feet per second, per second
t = time the ball takes to fall from its maximum
height to the ground, in seconds
First, divide the time you recorded by 2.
For example, if the projectile was in the air for 4 seconds, it spent 2 seconds going up and 2 seconds coming down. You need to know how long it took to come down.
Second, multiply the time (t) in seconds, by itself: t × t. For example, 2 × 2 = 4
Next, multiply your result by g, which is 32.2. For example, 4 × 32.2 = 128.8
Finally, divide your result in half to get h, the height of the projectile. For example, 128.8 ÷ 2 = 64.4 feet.
Questions to think about
What angle gives you the most height?
What things seem to affect the height of the projectile?
Who got the most height, and why?
Can you explain the winner using the laws of motion?
Why is horizontal motion not important when figuring out the height?
Try This!
Try dropping a projectile from a height you can measure, such as the height of a basketball hoop. Find the height using the time it takes to fall. How does it match your measurements? If you knew the height an object was dropped from, could you calculate how long it took to reach the ground?
What launch angle will send a projectile the greatest distance? Using a yardstick equipped with a protractor to measure angles, you can launch rubber bands to see,
›On a yardstick, mark a spot at about 22 inches.
›To attach a protractor to the yardstick, place the origin (the center dot or circle) of the protractor at the 22-inch mark. Align the protractor so that the 90-degree angle (the baseline) points along the yardstick, and that 0 degrees is perpendicular to the yardstick. Then secure the protractor to the yardstick with clear tape, being careful not to cover up the angles on the protractor.
›Make a loop of string. It should be long enough to hang 1 to 2 inches below the protractor from the origin.
›Place a pushpin at the origin. Hang the string on the pushpin.
›Tape a binder clip or other small weight to the bottom of the string.
›Choose a launch angle and record it in your engineering notebook. Hold the yardstick so that the string hangs freely across the protractor.
›Prepare your projectile. Loop a rubber band around the end of the yardstick farthest from the protractor.
›Fire your rubber band! Each time you launch a rubber band, be sure to stretch it the same amount. Place a mark on the yardstick to help you remember how far you stretched!
›Record several different launch angles! Make sure that you’re launching from the same height off the ground each time.
Questions to think about
Which launch angle gives your rubber band the greatest range?
Why is it important to keep the height of the launcher the same?
Why does the rubber band need to be stretched the same length each time?
What forces affect the rubber band when it’s in flight?
Try This!
Try stretching the rubber band a different amount. How does this affect the distance? What happens if you launch your rubber band projectile at 0 degrees or 90 degrees? Can you create a way to launch something other than a rubber band?
minutephysics fall through earth