O King, for traveling over the country, there are royal roads and roads for common citizens; but in geometry there is one road for all.
MENAECHMUS
(4th century B.C.), when his pupil Alexander the Great asked for a shortcut to geometry.
IN following the Belt along its length, we have lost the thread of time; and we now return to the Eastern Mediterranean, where the history of mankind went through a few inspiring centuries associated with the ancient Greeks. The Golden Age of this time was the age of the University of Alexandria; but just as the Alexandrian sun continued to glimmer some centuries after the Romans had sacked its places of learning and burned its libraries, so there was already some light before the city and its University were founded.
This was a time when the Greeks first held their own against the then all-mighty Persian Empire at Marathon (490 B.C.) and then defeated the Persians at Plataea (479 B.C.). This was also the time when democratic government developed; a slaveowners’ democracy, yes, but a democracy. The next 150 years saw the confrontation of Athens and Sparta, the thinkers against the thugs. The thugs always win, but the thinkers always outlast them.
In mathematics, which is but a mirror of the society in which it thrives or suffers, the pre-Athenian period is one of colorful men and important discoveries. Sparta, like most militaristic states before and after it, produced nothing. Athens, and the allied Ionians, produced a number of works by philosophers and mathematicians; some good, some controversial, some grossly overrated.
As far as the history of π is concerned, there were four men of this period who had some bearing on the problem: Anaxagoras, Antiphon, Hippocrates and Hippias.
Anaxagoras of Clazomenae (500-428 B.C.) found in Athens a bold new spirit of free enquiry and enthusiastically joined in with a truly scientific spirit, not shying away from experiment nor from popularizing science (both in diametrical opposition to the snobbism of the later Greek philosophers). He taught that the annual swelling of the Nile was due to the melting of mountain snows near the upper part of the river; that the Moon received its light solely from the Sun; that eclipses of the Moon or the Sun were caused by the interposition of the Earth or the Moon; that the Sun was a red-hot stone bigger than the entire Peloponnese; and other (less successful) theories. But in his theory of the Sun, which denied that the Sun was a deity, he had gone too far, and for some time he was imprisoned in Athens for impiety.
While in jail, he attempted to “square the circle,” a problem intimately connected with π, which requires the construction of a square equal in area to a given circle, but which we shall examine in more detail in the next chapter. It is apparently the first mention (by Plutarch) of this famous problem that fascinated men until 1882, when the proof that it could not be solved (by Greek geometry) was finally furnished; and even now it continues to fascinate amateur circle squarers who cannot be dissuaded by mathematical proof.
Another Greek of this period (late 5th century B.C.) associated with squaring the circle is the Sophist philosopher Antiphon, who enunciated the “principle of exhaustion,” which was to have a profound influence on mathematicians in their quest for the value of π until the invention of the calculus in the late 17th century. The exhaustion principle states the following: If a square is inscribed in a circle, and further regular polygons are inscribed with double the number of sides at each step (octagon, 16-sided polygon, etc.), until the circle is exhausted, then eventually a polygon will be reached whose sides are so short that it will coincide with the circle. This led Antiphon to believe that the circle could be squared by Greek geometry; for any polygon can be squared, and since the “eventual” polygon is equivalent to a circle, Antiphon judged that a circle could be squared also.
Antiphon’s principle is almost correct; it becomes completely correct in Euclid’s more cautious formulation, according to which the difference between the remaining area and that of the circle can be made smaller than any preassigned value, no matter how small (but not zero).

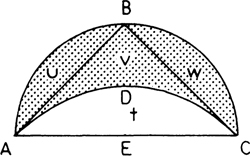
Hippocrates lune. The lower case letters stand for areas.
Another man associated with the area of circles during this period was Hippocrates of Chios, who should not be confused with his better known contemporary, the physician Hippocrates of Cos. Hippocrates of Chios was a merchant who came to Athens in 430 B.C. According to some, he lost his money through fraud in Byzantium, according to others he was robbed by pirates; in any case, he thereafter turned to the study of geometry, which is in itself remarkable, for in later years the road between business and science was more often traveled in the opposite direction.
Hippocrates was evidently the first to find the exact area of a figure bounded by curves, in this case circular arcs, and thus became the first man to make a precise statement on curvilinear mensuration. The area that Hippocrates squared (or triangled, but to square a triangle is trivial) was that of a lune (see figure above) bounded by the semicircular arc ABC circumscribed about the right-angled, isosceles triangle ABC, and the circular arc ADC such that the segment ADEC is similar to the segment AB. (That is, the radius of ADC is to AC as the radius EA is to AB.)
Hippocrates found that the area of this lune is exactly equal to the triangle ABC.
Proof: Since the segments above the three sides are similar, their areas are to each other as the squares of their bases; since by Pythagoras’ Thorem AB2 + BC2 = AC2, the areas of the corresponding segments are related by
![]()
The area of the lune is
![]()
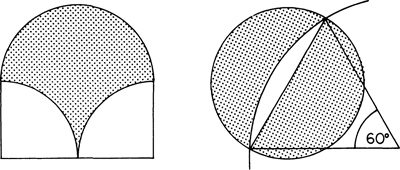
Examples of figures that are exactly squarable by Euclidean geometry. The shaded areas are reducable to Hippocrates lunes, and hence are squarable.
or on substituting (1),
![]()
i.e., it is equal to the area of the triangle.
This is probably not the proof given by Hippocrates, whose book on geometry has been lost. The proof of this theorem given by Eudoxos and taken over by Euclid more than a century later is a reductio ad absurdum (reduction to the absurd), a proof by contradiction or indirect proof. It is possible that Hippocrates was the first to use this method of proof, whose essence is this: If we want to prove that a statement is true, we first assume that it is not true and use this assumption to achieve an absurd result (or a result that contradicts the assumption); since the result is absurd, the premise must have been false; if a statement is either true or false (tertium non datur, there is no third possibility), the statement must be true.
For example, the fact that the number of primes (numbers divisible only by themselves or one) is infinite is proved as follows. Assume that the number of primes is finite. Then there must exist the largest prime, call it p. Now the number
![]()
is divisible by all integers up to and including p. Hence the number p! + 1 is divisible by none of them and is therefore a prime. But the prime p! + 1 is obviously greater than p, which contradicts the assumption that p is the largest prime. The assumption is therefore false, and the number of primes is infinite.
Hippocrates’ discovery can easily be generalized to many other curvilinear figures, two of which are shown above. The one on the right, in particular, must have raised high hopes of squaring the circle (or the semicircle, which is just as good). The snag, as we know today, is that some, but not all, lunes can be squared. In the top right figure, for example, the sum of the lune and the semicircle can be squared, but they cannot be squared individually — at least not by the Greek rules of the game (which will be discussed in the next chapter).
Very many other figures composed entirely or partly of Hippocrates lunes can be constructed. Leonardo da Vinci (1452-1519) was particularly fascinated by Hippocrates lunes, and he constructed 176 such figures on a single page of his manuscripts, and more elsewhere.19
It is ironic that the work of Antiphon and Hippocrates should have been brought to our attention by one whose teachings held up the progress of science for close to 2,000 years, the Greek philosopher Aristotle (384-322 B.C.). He judges both Antiphon’s principle of exhaustion and Hippocrates’ quadratures to be false, considering the refutation of Antiphon’s principle beneath the notice of geometers, and never, of course, achieving a disproof of Hippocrates’ quadrature of the lune, either. Aristotle, we are invaribly told, was “antiquity’s most brilliant intellect,” and the explanation of this weird assertion, I believe, is best summarized in Anatole France’s words: The books that everybody admires are the books that nobody reads. But on taking the trouble to delve in Aristotle’s writings, a somewhat different picture emerges (see also Chapter 6). His ignorance of mathematics and physics, compared to the Greeks of his time, far surpasses the ignorance exhibited by this tireless and tiresome writer in the many subjects that he felt himself called upon to discuss.
* * *
THE fourth man of interest in this early Greek period is Hippias of Elis, who came to Athens in the second half of the 5th century B.C., and who was the first man on record to define a curve beyond the straight line and circle. It is perhaps ironic that the next curve on the list should be a transcendental one, skipping infinitely many algebraic curves, but the Greeks did not yet know about degrees of a curve, and so they ate fruit from all orchards. The curve that Hippias discovered was called a trisectrix, because it could be used to trisect an angle (the second problem that fascinated antiquity, the third being the doubling of the volume of a cube), or a quadratrix, because it could be used to square the circle, and with the mere use of compasses and straightedge, too. There has to be a snag, of course, and the snag was that the construction violated another rule of the Greek game, but this point is deferred to the next chapter.
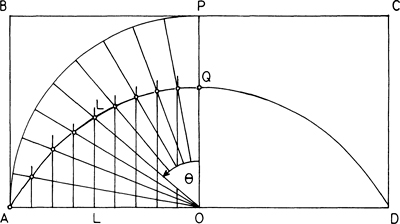
Hippias’ quadratrix
Hippias’ quadratrix was defined as follows. Let the straight segment AB move uniformly from the indicated position until it coincides with CD, and let the segment AO rotate uniformly clockwise about the point O from the indicated position through OP until it coincides with OD, in the same time as AB moves to CD. The curve traced by the intersection (L) of the two segments during this motion is Hippias’ quadratrix.
Using only compasses and straightedge, and discarding the concepts of motion and time, we can also construct this curve by dividing the angle AOP into 2n parts, and the segment AO into the same number of parts, where n is arbitrarily large. Any intersection of two corresponding segments is then a point on the quadratrix.
We do not know whether Hippias realized that by means of his curve the circle could be squared; perhaps he realized it, but could not prove it. The proof was later given by Pappus (late 3rd century A.D.), who evidently had it from Dinostratus (born about 350 B.C., brother of Menaechmus, who is quoted at the beginning of this chapter). His proof by elementary geometry is a reductio ad absurdum, but the modern road is shorter:
Let OL = ρ and OA = r; from the definition of the quadratrix, and expressing the angle of rotation in radian measure, we have
![]()
and since AL′ = r – ρ sin θ, we obtain
![]()
For θ → 0, we have (sin θ)/θ → 1, ρ → OQ ; also 2r = AD, so that (1) yields
![]()
and we have a geometrical construction for the circle ratio π.
To rectify the circle, we need a segment of length
![]()
or
![]()
so that u can be found by an easy construction of proportional quantites (similar triangles).
A rectangle with sides u/2 and r then has area
![]()
i.e., the same area as a circle with radius r, and since a rectangle is easily squared by an elementary construction, the circle is squared by the use of compasses and straightedge alone. Nevertheless, as we shall see, this construction failed to qualify under the implicit rules of Greek geometry.
* * *
HIPPIAS and Dinostratus only scratched the surface of this curve, for analytical geometry was still some 2,000 years away. But we might as well finish the job for them.
Let us regard (1) as the equation of the quadratrix in polar coordinates through
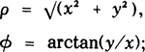
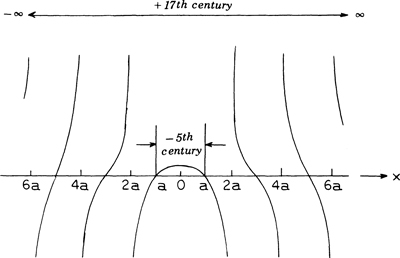
Hippias’ quadratrix derived by analytical geometry. Hippias knew only the part in the interval – a < x < a, i.e., the one shown in the preceding figure.
After some manipulation, we have
![]()
and the figure above shows how the quadratrix has bloomed. Hippias and Dinostratus only saw the tip of the iceberg for – r < x < r.
The circle can also be squared by the use of the Archimedean spiral, as we shall see.
The essence of Hippias’ trick was the fact that the limit of (sin θ)/θ for θ → 0 is unity. But there are other curves exploiting this limit, and these can also be used as quadratrices. Three more appeared in the 17th century after Descartes’ discovery of analytical geometry:
Tschirnhausen’s quadratrix,
![]()
Ozam’s quadratrix
![]()
and the cochleoid, which in polar coordinates is given by
![]()
But the problem has lost its fascination, and these curves have, for most people, faded into oblivion. However, when viewed as functions rather than curves, they are still making a living in electromagnetics, spectral analysis and information theory, occasionally moonlighting in statistics.