
What ye have done unto the last of my brethren, ye have done unto me
JESUS OF NAZARETH
THE fall of Rome in 476 A.D. marks the time when the literate barbarians of Rome were replaced by the illiterate barbarians of Germany, and this event is generally considered as the beginning of the Middle Ages.
Disaster was followed by catastrophe: The Roman Empire was followed by the Roman Church. In the Eastern or Byzantine Empire, the Roman Empire continued hand in hand with the Eastern Orthodox church for a thousand more years.
What made the bloody tyrants of the time accept Christianity is debatable. Perhaps they welcomed a religion that would teach their subjects to turn the other cheek, and that promised salvation for humility and eternal damnation for rebellion. Perhaps they were impressed by the unparalleled organization and iron discipline of the early Christians. What is certain is that once the mediaeval kings and emperors had adopted Christianity as the official faith, their executioners saw to it that nothing else was allowed.
And “nothing else,” of course, included science, the staunchest opponent of the Supernatural.
In the early days of civilization, science and religion were in the same hands, in the hands of the priests, who had a monopoly on learning. In Egypt, Babylon, the Yucatan, and everywhere else in the Belt, they were the timekeepers and surveyors, the astronomers and geometers. They soon learned that knowledge was power: power over the gullible and over the uneducated. Five thousand years ago, the Chaldaean priests knew how to predict an eclipse, and they would impress the uneducated with much mumbo-jumbo about the impending catastrophe. The Egyptian priests had nilometers in their temples, instruments that communicated with the Nile by secret, underground channels; they learned to predict the rising and falling of the Nile, and they would impress the uneducated with much much mumbo-jumbo about the imminent floods or recessions of the Sacred River.
Mathematics and mumbo-jumbo remained allied for a long time. Pythagoras, for example, was a mathematician to a much lesser degree than he was a mumbo-jumboist. He taught that one stood for reason, two for opinion, three for potency, four for justice, five for marriage, seven held the secret of health, eight the secret of marriage, the even numbers were female, the odd numbers male, and so on. “Bless us, divine number,” the Pythagoreans would incant to the number four, “who generatest Gods and men, O holy tetraktys, that containest the root and source of the eternally flowing creation.”37 Immerged in this mumbo-jumbo, Pythagoras discovered that 32 + 42 = 52, and that there were other triplets of numbers x, y, z that satisfy the relation x2 + y2 = z2. Translated into geometry, this led him to the theorem which is quite unjustly called after him, for it had been known to every rope-stretcher (surveyor) from the Nile to the Yang-Tse Kiang for a thousand years before Pythagoras’ witchcraft.38
But witchcraft is easier than mathematics; specialization set in, and mumbo-jumbo became more and more separated from mathematics. Those interested in knowledge took the path to science; others took the road to the occult, the mystic and the supernatural. Thousands of cults and religions developed. The vast majorities of these did not recruit converts by force; not even the Roman enslavers forced their religion on the peoples they had conquered. But in three major cases religion became militant, and its fanatics disseminated it by fire and sword, plunging large parts of humanity into prolonged nightmares of horror. They were mediaeval Christianity, mediaeval Islam, and modern communism. For communism is a religion, too, with its church (party), its priests, its scriptures, its rituals, its dogmas, and its liturgy; the communist claims about dialectical materialism being a science are just so much more mumbo-jumbo. Communism uses science for its own ends; Muslim science, especially mathematics, flourished (on the whole) under the rule of the Mohammedan fanatics; but mediaeval Christianity, in many ways the most terrible of the three catastrophies, persecuted science with torture chamber and the stake, and almost succeeded in extinguishing it completely.
Scientific research, wrote Tertullian (160-230), had become superfluous since the Gospel of Jesus Christ had been received. Tomaso d’Aquino (St. Thomas, 1225-1274) wrote that there was no conflict between science and religion; but by “science” he understood Aristotle’s tiresome speculations. The mediaeval Church never made St. Thomas’ mistake of confusing the two: It promoted Aristotle to some kind of pre-Christian saint, but (except for a very modest amount of third-rate work within its own cloisters) persecuted science almost wherever it appeared.
Scientific works and entire libraries were set to the torch kindled by the insane religious fanatics. We have already mentioned the Bishop of Yucatan, who burned the entire native literature of the Maya in the 1560’s, and Bishop Theophilus, who destroyed much of the remnants of the Library of Alexandria (391). The Christian Roman emperor Valens ordered the burning of non-Christian books in 373. In 1109, the crusaders captured Tripoli, and after the usual orgy of butchery typifying the crusades (though this one did not yet include the murderous Teutonic Knights), they burned over 100,000 books of Muslim learning. In 1204, the fourth crusade captured Constantinople and sacked it with horrors unparalleled even in the bloody age of the crusades; the classical works that had survived until then were put to the torch by the crusaders in what is generally considered the biggest single loss to classical literature. In the early 15th century, Cardinal Ximenes (Jimenez), who succeeded Torquemada as Grand Inquisitor and was directly responsible for the cruel deaths of 2,500 persons, had a haul of 24,000 books burned at Granada.*
In 1486, Torquemada sentenced the Spanish mathematician Valmes to be burned at the stake because Valmes had claimed to have found the solution of the quartic equation. It was the will of God, maintained the Grand Inquisitor of the Holy Office of the Inquisition Against Heretical Depravity, that such a solution was inaccessible to human understanding.39
Not only scientific theory was condemned as the work of the devil. The devil also seems to have known a lot more about navigation than the bloodthirsty Men of God. Many (perhaps most) ships sailing the Mediterranean in the Middle Ages had Jewish navigators, for the Christian captains and crews were not supposed to meddle with the devilish science of mathematics.40 In the 10th century, Raud the Strong, a Viking chieftain, escaped the fanatical Christianizing king of Norway Olaf Trygvasson by sailing into the wind (i.e., maintaining a zig-zag course whose average advances against the wind); the pious king, who was better acquainted with witchcraft than with the triangle of forces, thereupon accused Raud of being in alliance with the devil, and when he finally caught him, he had him killed by stuffing a viper down his throat.41

GIORDANO BRUNO (1548-1600)
The Middle Ages are usually considered to have ended with the fall of Constantinople (1453) or the discovery of the New World (1492); but the insane persecution of science continued well beyond that time, and it is difficult to give a date when it ceased. For more than a century longer, the Church tolerated no deviation from the literal word of the Bible, or from the teachings of its idol Aristotle. In 1600, Giordano Bruno was burned alive in Rome for claiming that the earth moves round the sun. In 1633, the 70-year old Galileo Galilei went through the torture chambers of the Inquisition until he was willing to sign that
I, Galileo Galilei,… aged seventy years, being brought personally to judgement, and kneeling before you Most Eminent and Most Reverend Lords Cardinals, General Inquisitors of the universal Christian republic against depravity … swear that … I will in future believe every article which the Holy Catholic and Apostolic Church of Rome holds, teaches, and preaches … I held and believed that the sun is the center of the universe and is immovable, and that the earth is not the center and is movable; willing, therefore, to remove from the minds of your Eminences, and of every Catholic Christian, this vehement suspicion [of heresy] rightfully entertained against me,… I abjure, curse and detest the said errors and heresies,… and I swear that I will never more in future say or assert anything verbally, or in writing, which may give rise to a similar suspicion of me … But if it shall happen that I violate any of my said promises, oaths and protestations (which God avert!), I subject myself to all the pain and punishments which have been decreed … against delinquents of this description.42
Thereupon he was sentenced to life imprisonment in a Roman dungeon. The sentence was later commuted and he died, a blind and broken man, in 1642. But not even in death did the pious inquisitors leave him in peace. They destroyed many of his manuscripts, disputed his right to burial in consecrated ground, and denied him a monument in the ludicrous hope that this brilliant thinker and his work would be forgotten. 250 years later, Sir Oliver Lodge commented:
Poor schemers! Before the year was out, an infant was born in Lincolnshire, whose destiny it was to round and complete and carry forward the work of their victim, so that, until man shall cease from the planet, neither the work nor its author shall have need of a monument.
* * *
SUCH was the ugly face of the Middle Ages. It is not surprising that mathematics made little progress; toward the Renaissance, European mathematics reached a level that, roughly, the Babylonians had attained some 2,000 years earlier43 and much of the progress made was due to the knowledge that filtered in from the Arabs, the Moors and other Muslim peoples, who themselves were in contact with the Hindus, and they, in turn, with the Far East.
The history of π in the Middle Ages bears this out. No significant progress in the method of determining π was made until Viète discovered an infinite product of square roots in 1593, and what little progress there was in the calculation of its numerical value, by various modifications of the Archimedean method, was due to the decimal notation which began to infiltrate from the East through the Muslims in the 12th century.
Arab mathematics came to Europe through the trade in the Mediterranean, mainly via Italy; ironically, the other stream of mathematics was the Church itself.44 Not only because the mediaeval priests had a near monopoly of learning, but also because they needed mathematics and astronomy as custodians of the calendar. Like the Soviet High Priests who publish Pravda for others but read summaries of the New York Times themselves, so the mediaeval Church condemned mathematics as devilish for others, but dabbled quite a lot in it itself. Gerbert d’Aurillac, who ruled as Pope Sylvester II from 999 to 1003, was quite a mathematician; so was Cardinal Nicolaus Cusanus (1401-1464); and much of the work done on π was done behind thick cloister walls. And just like the Soviets did not hesitate to spy on the atomic secrets of bourgeois pseudo-science, so the mediaeval Church did not hesitate to spy on the mathematics of the Muslim infidels. Adelard of Bath (ca.1075-1160) disguised himself as a Muslim and studied at Cordoba;45 he translated Euclid’s Elements from the Arabic translation into Latin, and Ptolemy’s Almagest from Greek into Latin. When Alfonso VI of Castile captured Toledo from the Moors in 1085, he did not burn their libraries, containing a wealth of Muslim manuscripts. Under the encouragement of the Archbishop of Toledo, a veritable intelligence evaluation center was set up. A large number of translators, the best known of whom was Gerard of Cremona (1114-1187), translated from Arabic, Greek and Hebrew into Latin, at last acquainting Europe not only with classical Greek mathematics, but also with contemporary Arab algebra, trigonometry and astronomy. Before the Toledo leak opened, mediaeval Europe did not have a mathematician who was not a Moor, Greek or a Jew.46

GALILEO GALILEI (1564-1642)
Discovered the law of the pendulum; radically improved the telescope; discovered the satellites of Jupiter, sunspots, the rotation of the Sun, and the libration of the Moon; proved the uniform acceleration of all bodies falling to earth; doubted the infinite velocity of light and suggested how to measure its velocity; established the concept of relative velocity. Above all, he discovered the laws of motion, though he was not yet able to formulate them quantitatively.
One of the significant mediaeval European mathematicians was Leonardo of Pisa (ca. 1180-1250), better known by his nickname Fibonacci (“son of Bonaccio”). Significantly, he was an Italian merchant, so that he worked within one of the Arabic infiltration routes. In 1202, he published a textbook using algebra and the (present) Hindu-Arabic numerals. He is best known for the Fibonacci sequence
![]()
where each number (after the initial 1’s) is the sum of the two preceding ones. This sequence turns up in the most surprising places (see figure here), and its applications range from the growth of pineapple cells to the heredity effects of brother-sister incest. There is a Fibonacci Quarterly in the United States in our own day, for the fertility of this sequence appears to be endless.
But Fibonacci also worked on π, though his progress on this point was not as impressive as his other achievements. Like Archimedes, Leonardo used a 96-sided polygon, but he had the advantage of calculating the corresponding square roots by the new decimal arithmetic. Theoretically, his work (published in Practica geometriae, 1220) is not as good as Archimedes’, whose approximations to the square roots are always slightly on the low side for the circumscribed polygon, and slightly on the high side for the inscribed polygon; since the square roots appeared in the denominator, this assured Archimedes of getting the correct bounds. Fibonacci used no such care, extracting the square roots as nearly as he could, but he was lucky: His bounds turned out to be more accurate than Archimedes’, and the mean value between them,
![]()
is correct to three decimal places.
Otherwise there was little progress. Gerbert (Pope Sylvester) used the Archimedean value π = 22/7, but in the next 400 years we also find the Babylonian 3 1/8 and the Egyptian π = (16/9)2 in various cloister correspondence.47 The documents of the time mostly show the low level of mediaeval mathematics. Franco von Lüttich, for example, wrote a long treatise on the squaring of the circle (ca. 1040), which shows that he did not even know how to square a rectangle47 (here), and Albert von Sachsen (died 1390) wrote a long treatise De quadratura circuli consisting for the most part of philosophical polemics. The crux of the problem is brushed away by saying that “following the statement of many philosophers,” the ratio of circumference to diameter is exactly 22/7; of this, he says, there is proof, but a very difficult one.47 Dominicus Parisiensis, author of Practica geometriae (1346), distinguishes himself above his contemporaries by at least knowing that π = 22/7 was an approximation. So did the Viennese Georg Peurbach (1423-1461), who knew Greek and some of the history of π; he understood Archimedes’ derivation of π > 22/7, and knew both the Ptolemeian π = 377 : 120, and the Indian value π = √10.
Perhaps the only interesting contribution of this sorry time is that of Cardinal Nicolaus Cusanus (1401-1464), a German who worked in Rome from 1448 until his death. Although his work on π was not very successful and his approaches were more ecclesiastic than mathematical,48 he did find a good approximation for the length of a circular arc. His derivation is somewhat tiresome,49 but in modern terminology, it amounts to
![]()
To find the quality of this approximation, we multiply (1) by (2 + cosθ) and expand both sides in series (even though Brook Taylor is still two and a half centuries away), obtaining
![]()
so that up to the third-order term the two expressions are identical, and the fifth order term differs only by 3/5. The approximation is therefore excellent for
![]()
for θ = 36°, the error is about 2 minutes of arc. Well done, Cardinal.
It is doubtful whether some two centuries later, the great Dutch physicist Christiaan Huygens (1629-1693) was familiar with Cusanus’ work, but in his treatise De circuli magnitude inventa, which we shall meet again in Chapter 11, he derived a theorem suggesting a construction for the rectification of a circular arc as shown in the figure below, and which makes arc AB ≈ AB′. The construction was first suggested by Snellius, and it is equivalent to the Cardinal’s approximation: We have
![]()
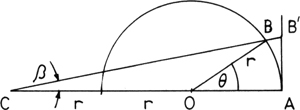
Approximate rectification of an arc suggested by one of Huygens’ theorems, and equivalent to Cardinal Cusanus’ approximation:
AB′ ≈ AB.
and from the triangle OCB,
![]()
From (3) we find tanβ, substitute in (2), and obtain after some trigonometric manipulation
![]()
If this is set equal to arc AB = rθ, it will be seen that Huygens’ construction is equivalent to Cusanus’ approximation (1).
But Huygens already lived in happier times.